【文化课学习笔记】【数学】导数(下)
【数学】导数(下)
导数的分类讨论
基本原理
导数的正负决定函数的单调性,所以可以根据导数的正负不同分类。
零点的个数会决定导数的正负分布区间的个数。
一般为了知道导数的正负区间,可以通过画图象的方法(一般需要画出单调性和零点)来求得。
所以分类讨论的标准如下:
- 讨论有无零点,有几个零点(等价于讨论函数类型)。
- 讨论零点是否在定义域内。
- 讨论零点之间的大小关系。
一次导数
适用范围:一次型函数。
原理:一次项系数不同 \(\longrightarrow\) 导数的正负也不同 \(\longrightarrow\) 导数正负分布不同 \(\longrightarrow\) 零点个数不同。
方法:讨论一次项系数的正负 \(+\) 零点是否在定义域内。
讨论一次项系数的正负,一般有以下三种情况:

其中第一幅图为一次项系数为正,第二幅为一次项系数为正,第三幅图一次项系数为 \(0\)。
当定义域不为 \(\mathrm R\) 时,还需要根据零点是否在定义域内进行分类讨论,如图所示:

结论:当零点在定义域内部时,一般导数有两个正负区间;当零点不在定义域内部时,一般导数只有一个正负区间。
对于一次项系数已知的函数,不需要分类讨论。
类一次导数
适用范围:最多只有一个零点的导数。
方法:分成有零点和没有零点两种情况讨论,如图所示:
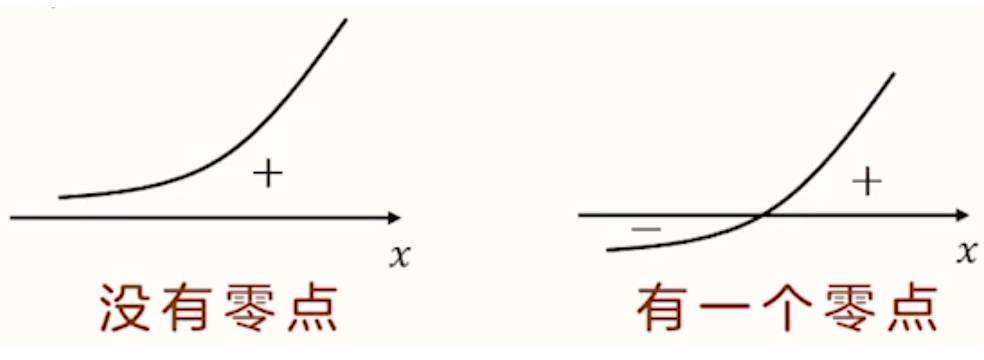
一般情况下需要通过讨论某个方程解的个数来讨论有无零点,例如导数 \(f'(x) = ae^x - 2\) 就可以通过解方程 \(ae^x =2\) 来判断零点个数。此时需要注意有些参数为 \(0\) 的情况,例如解上述方程,给两边同时除以 \(a\) 时,需要考虑 \(a\) 是否为 \(0\)。
二次导数
能因式分解
适用范围:二次型导数(能因式分解,且二次项系数可能为 \(0\))。
方法:讨论二次项系数的正负(\(+,-,0\))\(+\) 零点的大小关系(\(>,<,=\))\(+\) 零点是否在定义域内。
若函数求导后,导数是能分解的二次函数,则对于二次项系数不确定的题目,首先需要讨论二次项系数的正负。
注意:有的时候导数不一定是个二次函数,所以还需要讨论二次项系数是否为 \(0\)。
然后考虑先将其因式分解,按照两个零点的大小关系进行讨论,有三种情况:
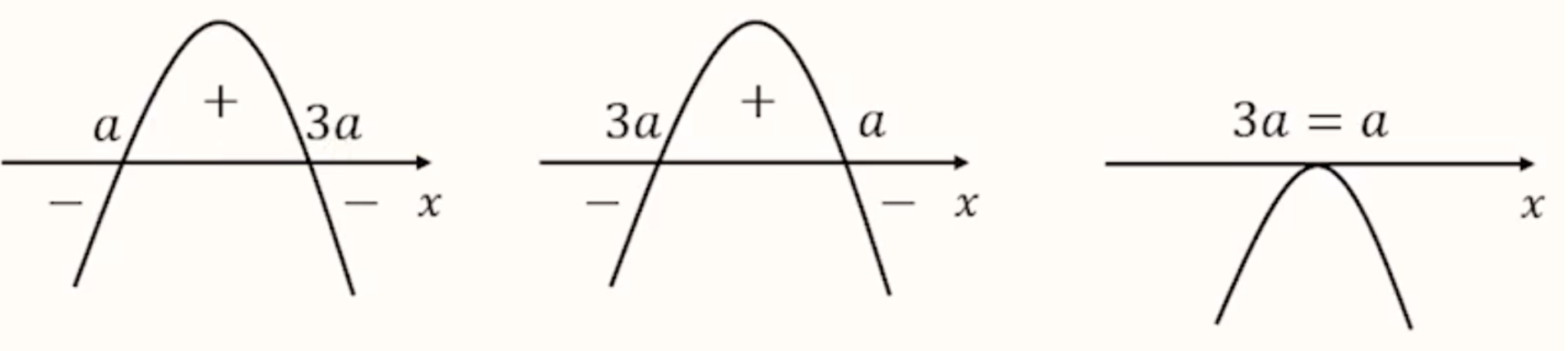
如图所示,若分解所得的两个解分别是 \(a\) 和 \(3a\),则分别按照 \(a < 3a\),\(a > 3a\) 和 \(a = 3a\) 分类讨论。
根据图象写出导数正负区间和函数单调区间即可。
当定义域不为 \(\mathrm R\) 时,还需要讨论零点是否在定义域内,如图所示:

对于需要同时讨论零点大小关系和零点是否在定义域内的情况,最好将两种情况的讨论先分别写出,然后再合并,分清楚之后再进行讨论。
本质:讨论有无零点,以及零点间的大小关系。
不能因式分解
类型:二次型导数(不能因式分解,且二次项系数可能为 \(0\))。
方法:讨论二次项系数(\(+,-,0\))\(+\) \(\Delta\)(\(\Delta \le 0,\Delta > 0\))\(+\) 零点是否在定义域内。
此时可以先通过前两种讨论求出零点,然后再考虑零点是否在定义域内。
判断零点是否在定义域的万能方法是使用韦达定理求出 \(x_1x_2\) 和 \(x_1 + x_2\) 再判断 \(x_1\) 和 \(x_2\) 的正负。
有时候也可以直接通过函数的特征、二次项系数的范围和定义域来直接判断。
例题:已知函数 \(f(x) = (ax^2 - a + 1)e^x(a \in \mathrm R)\),求函数 \(f(x)\) 的单调区间。
分析:
首先求出函数 \(f(x)\) 的定义域为 \(x \in \mathrm R\),导数为
由于 \(e^x >0\),所以只需要讨论 $g(x) = ax^2 + 2ax - a + 1 $ 的正负。
由于 \(g(x)\) 是一个二次型函数,且二次项系数不确定,所以先要讨论二次项系数的正负,即分为 \(a > 0,a < 0,a = 0\) 三种情况。
同时由于 \(g(x)\) 不能分解因式,所以考虑分类讨论 \(\Delta\) 的正负。
由于 \(\Delta = 4a^2 - 4a(-a + 1) = 8a^2 - 4a = 4a(2a - 1)\),所以当 \(\Delta \le 0\) 时,\(0 < a \le \dfrac 1 2\),当 \(\Delta > 0\) 时,\(a < 0\) 或 \(a > \dfrac 1 2\)。
合并上述两种分类讨论,则需要讨论 \(\begin{cases}0 < a \le \dfrac 1 2\\a = 0\\ a < 0\\ a > \dfrac 1 2\end{cases}\) 三种情况。
分类讨论如下:
当 \(a = 0\) 时,\(f'(x) = e^x > 0\),所以 \(f(x)\) 在 \(\mathrm R\) 上单调递增。
当 \(a \ne 0\) 时:
情况一:当 \(0 < a \le \dfrac 1 2\) 时,\(\Delta \le 0\),\(f'(x) \ge 0\),则 \(f(x)\) 在 \(\mathrm R\) 上单调递增。
情况二:
当 \(a < 0\) 时,\(\Delta > 0\),令 \(f'(x) = 0\),得 \(x = \dfrac{-2a \pm 2\sqrt{2a^2 - a}}{2a} = \dfrac{-a \pm \sqrt{2a^2 - a}}{a}\)。
所以 \(x_1= \dfrac{- a + \sqrt{2a^2 - a}}{a},x_2 = \dfrac{-a - \sqrt{2a^2 - a}}{a}\)。此时,\(x_1\) 的分子更大,但由于 \(a < 0\),所以 \(x_1 < x_2\)。
所以当 \(x \in \left(-\infty,\dfrac{-a + \sqrt{2a^2 - a}}{a}\right)\) 和 \(x \in \left(\dfrac{-a - \sqrt{2a^2 - a}}{a},+\infty\right)\) 时,\(f'(x) < 0\),所以 \(f(x)\) 单调递减;当 \(x \in \left(\dfrac{-a + \sqrt{2a^2 - a}}{a},\dfrac{-a - \sqrt{2a^2- a}}{a}\right)\) 时,\(f(x) > 0\),所以 \(f(x)\) 单调递增。
情况三:
当 \(a > \dfrac{1}{2}\) 时,\(\Delta > 0\),令 \(f'(x) = 0\),则解得的 \(x_1\) 和 $x_2 $ 同情况二,此时 \(x_1 > x_2\)。
所以当 \(x \in \left(-\infty,\dfrac{-a - \sqrt{2a^2 - a}}{a}\right)\) 和 \(x \in \left(\dfrac{-a + \sqrt{2a^2 - a}}{a},+\infty\right)\) 时,\(f'(x) < 0\),所以 \(f(x)\) 单调递减;当 \(x \in \left(\dfrac{-a - \sqrt{2a^2 - a}}{a},\dfrac{-a + \sqrt{2a^2- a}}{a}\right)\) 时,\(f(x) > 0\),所以 \(f(x)\) 单调递增。
其它类型导数
解题思路
对于能因式分解的导数先因式分解,然后对每一项求零点再根据零点结合导数分类讨论的基本原理进行分类讨论。
计算时需要注意,解对数不等式时,必须保证真数部分 \(> 0\)。
例题
已知函数 \(f(x) = (x-a)\sin x + \cos x,x \in (0,\pi)\)。当 \(a > \dfrac \pi 2\) 时,求函数 \(f(x)\) 的单调区间。
分析:
首先求导:
考虑将 \(x-a\) 和 \(\cos x\) 两段分开处理。
\(y = \cos x\) 在定义域即 \(x \in (0,\pi)\) 上时,当 \(0 < x < \dfrac \pi 2\) 时为正,当 \(\dfrac \pi 2 < x < \pi\) 上为负,零点为 \(x = \dfrac \pi 2\)。
\(y = x-a\) 的零点为 \(x = a\)。
然后需要考虑零点是否在定义域内,对于 \(y = \cos x\),其零点 \(x = \dfrac \pi 2\) 已经在定义域内;对于 \(y = x - a\),由于 \(a > \dfrac \pi 2\),且定义域为 \(x \in (0,\pi)\),所以当 \(\dfrac \pi 2 < a < \pi\) 时,零点在定义域内,当 \(a \ge \pi\) 时,零点不在定义域内。
最后考虑零点之间的大小关系,由于题目中已经确定 \(a > \dfrac \pi 2\),所以无需考虑。
接下来就可以根据 \(a\) 的取值范围分类讨论:
当 \(a \ge \pi\) 时,\(x - a <0\),所以只需要考虑 \(\cos x\) 的正负。所以 \(x \in \left(0,\dfrac \pi 2\right)\) 时,\(\cos x > 0\),此时 \(f'(x) < 0\),\(f(x)\) 单调递减;\(x \in \left(\dfrac \pi 2,\pi\right)\) 时,\(\cos x < 0\),\(f'(x) > 0\),\(f(x)\) 单调递增。
当 \(\dfrac \pi 2 < a < \pi\) 时,考虑找到一个与 \(f'(x) = (x - a)\cdot \cos x\) 同正负的函数 \(g(x)\),绘制出 \(g(x)\) 的图象来判断 \(f'(x)\) 的正负。这里只需要找到一个函数 \(g(x)\) 使得其正负分布与 \(y = \cos x\) 正负分布相同即可。当 \(g(x) = - x + \dfrac \pi 2\) 时,\(g(x)\) 与 \(\cos x\) 在 \((0,\pi)\) 上同正负。所以 \(f'(x)\) 与 \(F(x) = -(x-a)\left(x - \dfrac \pi 2\right)\) 在定义域上同正负。此时 \(F(x)\) 为二次函数,开口向下,有两个零点,定义域上有三个正负区间。
所以 \(x \in \left(0,\dfrac \pi 2\right)\) 和 \(x \in (a,\pi)\) 时,\(f'(x) < 0\),\(f(x)\) 单调递减;\(x \in \left(\dfrac \pi 2,a\right)\) 时,\(f'(x) > 0\),\(f(x)\) 单调递增。
总结&技巧:
当函数的正负分布不容易直接求解,且函数图象此时不易画出时,可以考虑构造一个在定义域上正负分布与所求函数相同的函数,绘制出新函数的图像然后再求解。
一般情况下,若所求函数有两个正负区间,则可以考虑替换成一次函数,例如本题中的 \(y = \cos x\);若所求函数有三个正负区间,则可以考虑替换成二次函数。
这里正负替换的过程不应该写在卷面上。
恒成立与存在性问题
解题思路
方法一
转化法。首先需要将原不等式转化为不等式一边为函数,一边为常数的形式。
对于恒成立问题:
\(f(x) \ge a\) 恒成立 \(\iff\) \(f(x)_{\min} \ge a\)。
\(f(x) \le a\) 恒成立 \(\iff\) \(f(x)_{\max} \le a\)。
对于存在性问题:
\(\exist ~x\) 使得 \(f(x) \le a\) 恒成立 \(\iff\) \(f(x)_{\min} \le a\)。
\(\exist ~x\) 使得 \(f(x) \ge a\) 恒成立 \(\iff\) \(f(x)_{\min} \ge a\)。
若此时 \(f(x)_{\max}/f(x)_{\min}\) 能直接求出来,则考虑直接求出最大/最小值,然后解关于参数的不等式。
若求 \(f(x)_{\max}/f(x)_{\min}\) 时,发现函数单调增/减,没有最大值,思路上可以用极限分析代替取最大值。若分析完极限发现结论不成立,则可以利用取特殊点的方式来证明。
注意:这种方法下有时候不一定要求出 \(f(x)\) 的单调性,只需要求出其最大值/最小值的正负,或某个点的正负即可。
方法二
参变分离。
通过移项,将带参的部分放在不等式的左边,将不带参的部分放在不等式的右边。然后转化为有关参数 \(a\) 的不等式,解不等式,转化为参数小于等于或大于等于某式,将该式当作函数 \(g(x)\),则如果是恒成立问题,则问题转化为 \(a \le g(x)_{\min}\) 或 \(a \ge g(x)_{\max}\);如果是存在性问题则问题转化为 \(a \le g(x)_{\max}\) 或 \(a \ge g(x)_{\min}\)。求出 \(g(x)_{\min}/g(x)_{\max}\) 即可求出参数 \(a\) 的取值范围。
两种方法选择的标准:哪种方法导数更容易研究,就选哪种方法。
当不能看出哪种情况更容易时,优先选择参变分离。一般情况下参变分离会更简单,因为方法一中求的是 \(f(x)\) 的最值,有参数,可能会存在参数的分类讨论,比较麻烦;方法二求的是 \(g(x)\) 的最值,是一个确定的函数,不存在参数的分类讨论,所以更简单。
有关结构相同的不等式的处理
这种技巧在「函数 - 指对函数实战演练 - 解题技巧」中曾提到过,这里再提一次是为了跟导数结合,将此类不等式转化成恒成立问题。
对 \(\forall x_1,x_2,\dfrac{f(x_1) - f(x_2)}{x_1 - x_2} > a\) 恒成立的处理:
设 \(x_1 < x_2\),则:
令 \(g(x) = f(x) - ax\),所以 \(g(x_1) > g(x_2)\),由于对任意 \(x_1,x_2\) 均成立,所以 \(g(x)\) 单调递增,所以 \(g'(x)\) 恒大于 \(0\)。
所以此类不等式可以转化为函数单调性,再转化为恒成立问题求解。
例题
例 1:已知函数 \(f(x) = \ln x + ax + 1,a \in \mathrm R\)。若不等式 \(f(x) \le 0\) 恒成立,求 \(a\) 的取值范围。
解法一
问题可以转化为 \(f(x)_{\max} \le 0\),所以首先考虑能不能求出 \(f(x)_{\max}\)。
函数定义域为 \(x \in(0,+\infty)\),求函数最大值考虑先求导然后判断正负。
那么有:
此时分母上的 \(x\) 恒大于 \(0\),只需要考虑分子的正负。
一次导数考虑先讨论 \(a\) 的正负。
当 \(a \ge 0\) 时,\(f'(x) > 0\),所以 \(f(x)\) 在定义域上单调递增,当 \(x \to +\infty\) 时,\(\lim \limits_{x \to +\infty} \ln x = +\infty,\lim \limits_{x \to +\infty} = \begin{cases} +\infty,a > 0\\0,a = 0\end{cases}\),所以 \(\lim \limits_{x \to +\infty} f(x) = +\infty\)。发现不符合要求 \(f(x)_{\max}\le 0\),所以考虑取 \(x = 1\),代入 \(f(x)\),得 \(f(1) = a + 1 > 0\),所以 \(f(x) \le 0\) 不恒成立,舍去。
当 \(a < 0\) 时,令 \(f'(x) = 0\),得 \(x = - \dfrac 1 a\)。所以 \(x \in \left(0,- \dfrac 1 a\right)\) 时,\(f'(x) > 0\),\(f(x)\) 单调递增;\(x \in \left(- \dfrac 1 a, + \infty\right)\) 时,\(f'(x) <0\),\(f(x)\) 单调递减。所以 \(f(x)_{\max} = f\left(- \dfrac 1 a\right) = \ln\left(- \dfrac 1 a\right) \le 0\),所以 \(0 < - \dfrac 1 a \le 1\),解得 \(a \le -1\)。
综上所述,\(a\) 的取值范围是 \((-\infty,-1]\)。
解法二
根据题意有
令 \(g(x) = - \dfrac{\ln x + 1}{x}\),其中 \(x > 0\),则 \(a \le g(x)_{\min}\)。
那么对 \(g(x)\) 求导:
分母 \(x^2\) 恒大于 \(0\),所以只需要考虑 \(\ln x\) 的正负。
则 \(x \in (0 , 1)\) 时,\(\ln x < 0\),\(g'(x) < 0\),所以 \(g(x)\) 单调递减;\(x \in (1,+\infty)\) 时,\(g'(x) > 0\),所以 \(g(x)\) 单调递增。
那么函数在 \(x = 1\) 上取到最小值,此时 \(g(x)_{\max} = g(1) = -1\),所以 \(a \le -1\)。
例 2:已知 \(a\) 为实数,函数 \(f(x) = a\ln x + x^2 - 4x\),\(g(x) = (a - 2)x\),若 \(\exist~x \in \left[\dfrac 1 e,e\right]\),使得 \(f(x) \le g(x)\) 成立,求实数 \(a\) 的取值范围。
分析:优先考虑参变分离法。
首先考虑对不等式变形:
令 \(h(x) = x - \ln x\),则 \(x \in (0,+\infty)\),则 \(h'(x) = 1 - \dfrac 1 x = \dfrac{x-1}{x}\)。
则 \(x \in (0,1)\) 时,\(h'(x) < 0\),\(h(x)\) 单调递减;\(x \in (1,+\infty)\) 时,\(h'(x) >0\),\(h(x)\) 单调递增。
所以 \(h(x)_{\min} = h(1) = 1 > 0\),所以 \(g(x) = x - \ln x > 0\)。
所以对 \((1)\) 式两边同时除以 \(x - \ln x\),得:
设 \(m(x) = \dfrac{x^2 - 2x}{x - \ln x}\),则 \(a \ge m(x)_{\min}\)。
对 \(m(x)\) 求导:
其中分母 \((x - \ln x)^2\) 在定义域内恒正,又由于 \(x \le e\),所以 \(\ln x \le 1\),所以 \(x + 2 - 2 \ln x = 2 + 2(1 - \ln x) >0\)。所以 \(m'(x)\) 的正负只取决于 \(x - 1\) 的正负。
则 \(x \in \left(\dfrac 1 e,1\right)\) 时,\(m'(x) < 0\),\(m(x)\) 单调递减;\(x \in (1,e)\) 时,\(m'(x) > 0\),\(m(x)\) 单调递增。
所以 \(m(x)_{\min} = m(1) = -1\),所以 \(a \ge -1\)。
例 3:已知函数 \(f(x) = \ln (ax + b) + x^2(a \ne 0)\)。若 \(f(x) \le x^2 + x\) 恒成立,求 \(ab\) 的最大值。
分析:
先对不等式变形:
令 \(g(x) = x - \ln (ax + b)\),则 \(g(x) \ge 0\),可转化为 \(g(x)_{\min} \ge 0\)。
考虑定义域,需要满足 \(ax + b > 0\),则 \(ax > -b\),发现 \(a\) 的正负不同时,定义域不同,所以考虑分类讨论 \(a\) 的正负。
当 \(a >0\) 时:
此时定义域为 \(x \in \left(- \dfrac b a,+\infty\right)\)。对 \(g(x)\) 求导:
分子恒大于 \(0\),所以只需考虑分母的正负。
令 \(ax + b - a = 0\),则 \(x = \dfrac{a - b}{a}\),所以 \(g'(x)\) 的零点是 \(x = \dfrac{a - b}{a}\),接着考虑零点是否在定义域内。
由于零点 \(x = \dfrac{a - b}{a} = 1 - \dfrac b a > - \dfrac b a\),所以零点在定义域内。
那么 \(x \in \left(- \dfrac b a,\dfrac{a - b}{a}\right)\) 时,\(g'(x) < 0\),\(g(x)\) 单调递减;\(x \in \left(\dfrac{a - b}{a},+\infty\right)\) 时,\(g'(x) > 0\),\(g(x)\) 单调递增。
所以
令 \(h(a) = a^2 (1 - \ln a)\),则 \(ab \le h(a)\),由于要求 \(ab\) 最大,所以 \(ab\) 的最大值即为 \(h(a)\) 的最大值。
考虑对 \(h(a)\) 求导:
由于 \(a > 0\),所以 \(h'(a)\) 的正负取决于 \(1 - 2 \ln a\) 的正负。
令 \(h'(a) = 0\),则 \(1 - 2\ln a = 0\),所以 \(a = e^{\frac 1 2}\)。则 \(a \in \left(0,e^{\frac 1 2}\right)\) 时,\(h'(a) > 0\),\(h(a)\) 单调递增;\(a \in \left(e^{\frac 1 2}, + \infty\right)\) 时,\(h'(a) < 0\),\(h(a)\) 单调递减。所以 \(h(a)_{\max} = h\left(e^{\frac 1 2}\right) = e(1 - \ln e^{\frac 1 2}) = \dfrac 1 2 e\)。
所以 \(ab\) 的最大值为 \(\dfrac 1 2 e\)。
当 \(a < 0\) 时:
此时定义域为 \(x \in \left(- \infty,- \dfrac b a\right)\),此时 \(g(x)\) 在 \(\left(- \infty,- \dfrac b a\right)\) 上单调递增。
当 \(x \to -\infty\) 时,\(g(x) \to -\infty\),所以 \(g(x)_{\min} \ge 0\) 不成立。考虑取点,由于 \(ax + b\to +\infty\),\(\ln(ax + b) \to +\infty\),根据 \(g(x)\) 的表达式可知需要取一个点满足 \(\begin{cases}x < 0\\ \ln(ax + b) > 0\end{cases}\),可解得 \(x < \dfrac{1 - b}{a}\)。
取 \(x_0\),满足 \(x_0 < 0\) 且 \(x_0 < \dfrac{1 - b}{a}\),所以 \(ax_0 > 1 - b\),所以 \(g(x_0) < 0\),不符合 \(g(x) \ge 0\) 恒成立,舍去。
综上所述,\((ab)_{\max} = \dfrac 1 2 e\)。
总结&技巧:
- 此题需要在定义域开始分类讨论。
- 对于类似此题两个参数的问题,可以通过消元的方式变成一个参数然后求解。
- 使用「取点法」求证恒成立不满足时,如果直接不好取点,可以考虑列出对应的点 \(x_0\) 所需要满足的不等式然后解不等式求解。
导数的零点问题
解题方法
研究 \(f(x)\) 的零点个数
- 研究 \(f(x)\) 的单调性:一个单调区间上,最多只有一个零点。
- 在每个单调区间 \([a,b]\) 上研究有没有零点:利用零点存在性定理,计算出 \(f(a)\cdot f(b)\) 的正负。
- $f(a)\cdot f(b) < 0 \implies $ 有 \(1\) 个零点。
- $f(a) \cdot f(b) > 0 \implies $ 有 \(0\) 个零点。
- \(f(a) = 0\) 或 $f(b) = 0 \implies $ 有 \(1\) 个零点。
对于有些带参函数,可以考虑参变分离之后转化为量函数的交点(一般其中一个函数图象为水平直线居多),例如求函数 \(f(x) = \ln x - ax\) 的零点个数,可以转化为研究 \(g(x) = \dfrac{\ln x}{x}\) 和 \(y = a\) 的交点个数。
对于 \(2\) 中,若端点 \(a\) 或 \(b\) 上的函数值不能直接求出,则考虑研究极限。例如:若单调区间为 \([a,+\infty)\),则研究 \(x \to +\infty\) 时,\(f(x)\) 的极限。极限法依旧不能直接写在卷面上,需要利用「取点法」代替极限。
对于「存在几个(条)」的存在性问题,如果条件可以转化成一个方程,那可以将问题转化为研究方程的零点个数(零点问题)。
求极限
对于简单的函数,即可以直接画出函数图象的函数,直接通过画图象来观察极限。
对于复杂函数(简单函数通过加减乘除得到):
- 分别求每个部分的极限。
- 对每个部分的极限做加减乘除。
关于不同无穷的大小(在函数中提到过):\(x \to +\infty\) 时,\(\ln x < x^n < e^x\)。
有以下几种类型:
【类型一:可以直接比较的】直接将每一部分的极限相加减即可。
【类型二:需要比较无穷大小的】
- 正无穷 \(+\) 负无穷:最终的极限取决于「最大的无穷」。
- $\dfrac{大无穷}{小无穷} = $ 无穷;\(\dfrac{小无穷}{大无穷} = 0\)。
【类型三:洛必达法则】
适用范围:\(\dfrac 0 0\) 或 \(\dfrac{\infty}{\infty}\) 型(看不出哪个无穷更大)极限。
内容:
当 \(x \to a\) 时,\(f(x),g(x) \to 0\) 或 \(f(x),g(x) \to +\infty\),则
有时候得到的 \(\lim \limits_{x \to a} \dfrac{f'(x)}{g'(x)}\) 依然不能直接看出其极限,需要再次使用洛必达法则。
例如:求 \(f(x) = \dfrac{x}{e^x - 1},x \to 0\) 的极限。
求解:
需要注意两类极限:
- 趋于无穷:可以将其理解为绝对值极大的数处理。
- 趋于 \(0\):可以将其理解为绝对值极小的数处理。
一个趋于 \(0\) 的函数取倒数,会趋于 \(+\infty\),例如 \(x \to 0\) 时,\(\dfrac{1}{x} \to +\infty\)。
例题
例 1:已知函数 \(f(x) = \dfrac {x^2} 2 - k\ln x,k > 0\)。若 \(f(x)\) 存在零点,求 \(k\) 的范围?
分析:
首先求出函数定义域为 \(x \in (0,+\infty)\)。再对 \(f(x)\) 求导:
\(x \in \left(0,\sqrt k\right)\) 时,\(f'(x) < 0\),\(f(x)\) 单调递减;\(x \in \left(\sqrt k ,+\infty\right)\) 时,\(f'(k) > 0\),\(f(x)\) 单调递增。
所以此时 \(f(x)_{\min} = f\left(\sqrt k\right) = \dfrac k 2 - k \ln \sqrt k\)。
由于 \(f(x)\) 存在零点,所以 \(f(x)_{\min} = \dfrac k 2 - k\ln \sqrt k \le 0\),求得 \(k \ge e\)。
又由于 \(f(x)_{\min} \le 0\) 时不一定保证存在零点,还需要验证存在一点 \(x_0 \in (0,+\infty)\) 使得 \(f(x_0) >0\)。所以考虑取 \(x_0 = 1\),此时 \(f(1) = \dfrac 1 2 > 0\),所以 \(k\ge e\) 是函数 \(f(x)\) 存在零点。
总结&技巧:
对于此题,\(f(x)\) 存在零点可以推出 \(f(x)_{\min} \le 0\),但是 \(f(x)_{\min} \le 0\) 却不一定能够使得 \(f(x)\) 存在零点。所以需要验证存在一点 \(x_0\) 属于定义域,使得 \(f(x_0) > 0\)。
所以证明题只需要每一步推理正确即可,而求取值范围必须保证等价。
例 2:已知函数 \(f(x) = \ln x - ax,a \in \mathrm R\)。讨论函数的零点个数。
分析:
所以问题转化为研究 \(g(x) = \dfrac{\ln x}{x}\) 和 \(y = a\) 的交点个数。
先对 \(g(x)\) 求导:
所以 \(x \in (0,e)\) 时,\(g'(x)>0\),\(g(x)\) 单调递增;\(x \in (e,+\infty)\) 时,\(g'(x) < 0\),\(g(x)\) 单调递减。
所以 \(g(x)_{\max} = g(e) = \dfrac 1 e\)。又因为当 \(x \to +\infty\) 时,\(g(x) \to 0\),当 \(x \to 0\) 时,\(g(x) \to -\infty\)。所以可绘制 \(g(x)\) 的函数图象如下:
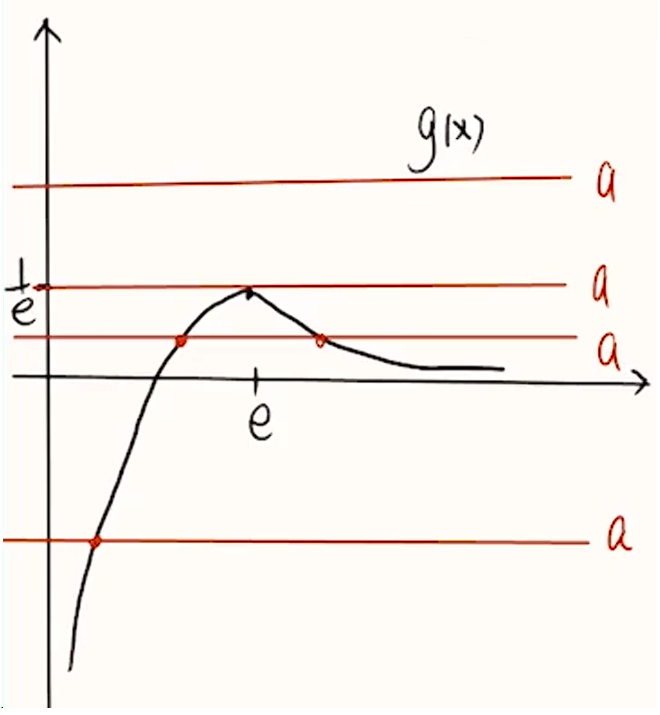
则 \(a > \dfrac 1 e\) 时,有 \(0\) 个零点;\(a = \dfrac 1 e\) 或 \(a \le 0\) 时,有 \(1\) 个零点;\(0 < a < \dfrac 1 e\) 时,有 \(2\) 个零点。
总结&技巧:
- 对于带参函数的零点问题,可以考虑参变分离后转化为函数交点问题。
- 已知单调性绘制函数图象时,要善用最值和极限。
例 3:已知函数 \(f(x) = x - 1 + e^x\),曲线 \(y = f(x)\) 与直线 \(y = kx -1\) 没有公共点,求 \(k\) 的取值范围。
分析:
由于曲线 \(y = f(x)\) 与直线 \(y = kx -1\) 没有公共点,所以可以转化为 \(f(x) = kx -1\) 无解,即 \(x+e^x = kx\) 无解。
那么有三种求解思路。
解法一
方程 \(x + e^x = kx\) 可以转化为 \(e^x = (k - 1)x\),即 \(y = e^x\) 与 \(y = (k - 1)x\) 无公共点,考虑数形结合。
先画出 \(y = e^x\) 的图象如下:
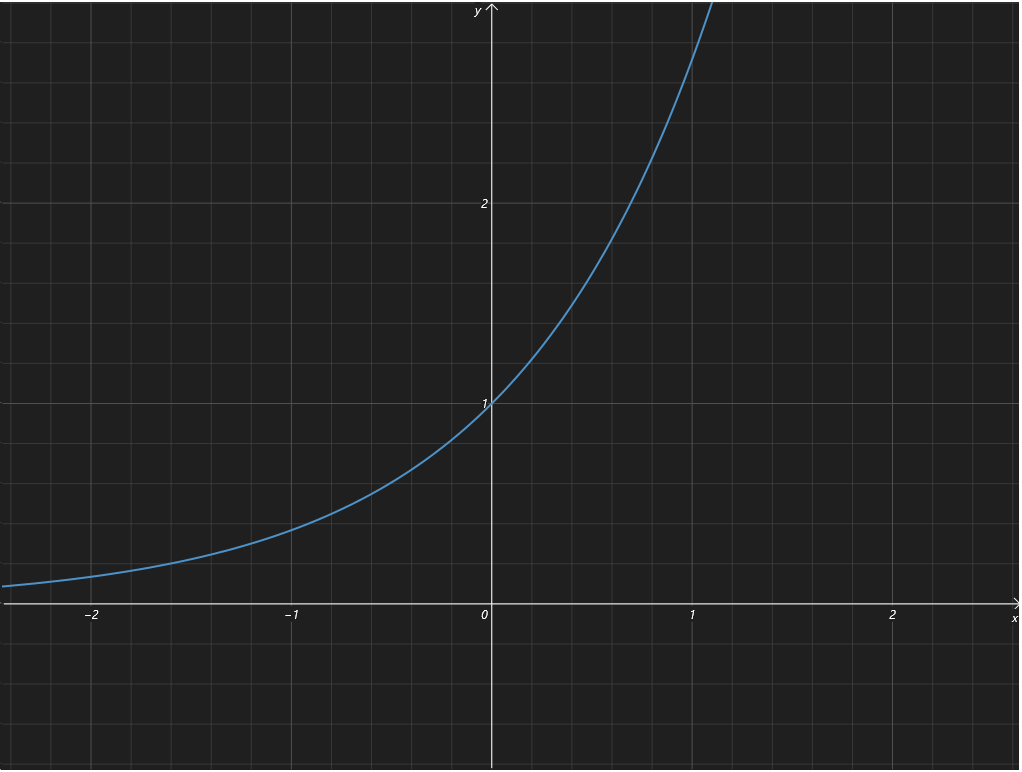
由于 \(y = (k - 1)x\) 经过原点,所以问题转化为 \(y = e^x\) 与一条经过原点的直线无交点。
那么通过画图可知,直线斜率应该大于等于 \(0\) 小于 \(y = e^x\) 过原点的切线斜率。
可求得切线斜率为 \(k' = e\)。所以 \(0 \le k-1 < e\),得到 \(1 \le k < e + 1\)。
注意:
此方法的好处是极快又准,但是不能用于解答题,因为有一些结论是从图中直接看出的,并没有合适的依据。所以此方法只适用于选择填空。
解法二
将问题转化为 \(e^x - (k - 1)x = 0\),即 \(g(x) = e^x - (k - 1)x\) 无零点。
考虑对其求导:
则当 \(k \le 1\) 时,\(g'(x) > 0\),\(g(x)\) 在 \(\mathrm R\) 上单调递增。
- 当 \(k < 1\) 时,\(x \to +\infty\),此时 \(g(x) \to +\infty\);\(x \to -\infty\),\(g(x) \to - \infty\)。所以 \(g(x)\) 有零点。
- 当 \(k = 1\) 时,\(g(x) = e^x > 0\),\(g(x)\) 无零点。
当 \(k > 1\) 时,令 \(g'(x) = 0\) 得 \(x = \ln (k - 1)\)。
所以 \(x \in (-\infty,\ln (k - 1))\) 时,\(g'(x) < 0\),\(g(x)\) 单调递减;\(x \in (\ln (k - 1),+\infty)\) 时,\(g'(x) > 0\),\(g(x)\) 单调递增。
所以
- 当 \(g(x)_{\min} > 0\) 即 \(1 < k < e + 1\) 时,\(g(x)\) 无零点。
- 当 \(g(x)_{\min} = 0\) 即 \(k = e + 1\) 时,\(g(x)\) 有唯一零点 \(x = \ln (k - 1) = 1\)。
- 当 \(g(x)_{\min} < 0\) 即 \(k > e + 1\) 时,当 \(x \to +\infty\) 时,\(g(x) \to +\infty\),根据「零点存在性定理」可知有零点。或取 \(g(0) = 1 > 0\),所以有零点。
综上,\(k\) 的取值范围为 \([1,e + 1)\)。
总结&技巧:
- 分析极限时,系数为 \(0\) 的情况,通常要拿出来单独讨论,例如本题的 \(k = 1\)。
- 最后一步求得 \(g(x)_{\min} < 0\) 时,必须利用极限/取点根据「零点存在性定理」判定有零点,否则过程不严谨。
解法三
将方程转化为 \(1 + \dfrac{e^x}{x} = k(x \ne 0)\),即函数 \(y = \dfrac{e^x}{x}\) 与水平直线 \(y = k\) 无交点,此时需要分类讨论 \(x = 0\) 的情况。
则当 \(x = 0\) 时,代入发现方程不成立,舍去。
当 \(x \ne 0\) 时,\(k = 1 + \dfrac{e^x}{x}\)。设 \(g(x) = 1 + \dfrac{e^x}{x}\),对 \(g(x)\) 求导:
\(x^2\) 和 \(e^x\) 恒大于 \(0\),则只需要讨论 \(x - 1\) 的正负。
当 \(x \in (-\infty,0)\) 和 \(x \in (0,1)\) 时,\(g'(x) < 0\),\(g(x)\) 单调递减。
当 \(x \in (1,+\infty)\) 时,\(g'(x) > 0\),\(g(x)\) 单调递增。
由于 \(g(1) = 1 + e\),所以:
- \(x \to +\infty\) 时,\(g(x) \to +\infty\)。
- \(x \to 0^+\) 时,\(g(x) \to +\infty\)。
- \(x \to 0^-\) 时,\(g(x) \to -\infty\)。
- \(x \to -\infty\) 时,\(g(x) \to 1\)。
这里的 \(0^+\) 表示极小的正数(趋于 \(0\) 的正数);\(0^-\) 表示极小的负数(趋于 \(0\) 的负数)。
注意:
这种方法求导后讨论 \(g(x)\) 单调性时,需要注意 \(x = 0\) 不在定义域内,所以原函数有三个单调区间而不是两个单调区间。
由于单调区间的不同,所以 \(x \to 0^+\) 和 \(x \to 0^-\) 也要看成两种极限分别讨论。
讨论极限时,对于 \(x \to -\infty\) 的情况,此时 \(e^x\) 趋于 \(0\),\(x\) 趋于 \(-\infty\),所以二者相除是一个 \(<0\) 的绝对值极小的数,用 \(1\) 加上它,会趋于 \(1\),所以 \(y = 1\) 是函数的一条渐近线。
根据极限讨论可绘制函数图象如下: