【物理】牛二力学
牛顿第二定律
公式
F 合 = ma
其中 F 合
方向
F 合 a
牛二正交分解
建系:建立合适的坐标系,让尽可能多的力在坐标轴上。一般以 a x a y 。(这样可以保证 y
分解:分解不在坐标轴上的力。
列式:对于某方向平衡时 :上 = 下 或 左 = 力;对于某方向不平衡时 ,F 合 = 大 − 小
求解拉力作用最短时间的方法技巧
定义:位移 x 0
运动过程:
匀加速直线运动:从起点出发,到撤去外力前;
匀减速直线运动:从撤去外力开始,到最后静止。
方法:
对「撤去外力前」的物体进行受力分析,求得加速过程中的加速度 a 1
对「恰好撤去外力时」的物体进行受力分析,求得减速过程中的加速度 a 2
画出「整个运动过程」的 v − t
设所求为 t t
【模型】弹簧运动模型
判断加速/减速的方法:看 a , v a , v → a , v →
其中加速度 a F 合 v
过程分析:
物体刚接触到弹簧时:受到较大 的重力 G 较小 的弹簧弹力 F N F 合 a v
从物体接触到弹簧到向下运动(F N < G 较大 的重力 G 较小 的弹簧弹力 F N F N x F 合 a v 加速度减小 的加速运动。
临界点(F N = G F N G F 合 = 0 a = 0 v 最大值 。
从临界点到速度减小为 0 较小 的重力 G 较大 的弹簧弹力 F N F N x F 合 a v 加速度增大 的减速运动。
速度减小为 0 F N F 合 v = 0
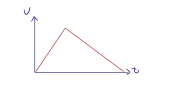
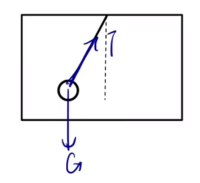
【模型】绳子倾角模型
问题模型:如图,已知绳子倾角 θ a
受力分析:小球受自身重力 G T
所以根据受力分析可以求出物体的加速度 a g tan θ
问题:
运动状态:根据受力分析可知,F 合 v v
对于与之相关的其他物体的受力分析:根据小球的 F 合 a
斜面多段运动
将整个运动分为多过程,对于每个过程都进行受力分析,计算求解。
有关牛二运动学基础计算的常见易错点及注意事项
f = μ F N F N f μ 代入值计算时,例如 a = μ g g
对于有斜面的问题时,若题目求得是高度 不要求成长度 。
当某物体从斜面上冲上,到达最高点,判断能否下滑时,应该判断 μ tan θ
当 μ < tan θ
当 μ ≥ tan θ
对于与运动学结合的题目,要善用速度位移公式 2 a x = v 2 − v 0 2
超重与失重
超重
加速度 a
失重
加速度 a
当加速度 a = g
解题技巧及注意事项
受力分析时一般分析与其他物体接触最少的物体。
对于「某人在地面上最多能举起质量为 80 kg 800 N
加速度 a F 合
单物体弹簧突变
特点
弹簧弹力无法突变。
原因:F = k Δ x F x F
解题方法
计算弹簧弹力;
把弹簧弹力看成外力,重新受力分析。
易错点及注意事项
受力分析得到的 F 合 = ma m 2 m m
若剪断弹簧 ,则弹簧的弹力变为 0
遇到需要正交分解求解加速度的问题,可以考虑受力分析时正交分解和力的合成求出 F 合
对于未知物体状态(运动还是静止)的题目求摩擦力,首先应该判断物体受静摩擦还是滑动摩擦(或者物体的运动状态)。
分解加速度
建系优先级
若题目所求的两个力相互垂直,则按照这两个力的方向为坐标轴建系。注意:此时需要分解不在坐标轴上的所有物理量 ,例如除了力还可能有加速度 a
否则按照加速度 a
多物体牛二
解题思路
先后顺序:首先考虑接触面少的物体进行受力分析。
相互作用:画出与已分析的物体会产生相互作用的力的物体对应的力。
不断重复第二步。
解题方法——整体法
【使用条件】加速度 a
【目的】快速求加速度 a
做题时,一般可以先考虑能否用整体法,优先考虑整体法,再考虑隔离法 。
【模型】一静一动模型
含义:一个物体平衡(加速度为 0 0 0 0
求解:按照上述解题方法进行受力分析列式求解。
【模型】连接体
推导
其中模型一 ~ 模型五属于同一类(绳子时直的),模型六~模型八属于同一类(绳子是弯的)。
一般前一类可以用整体法,后一类一般只能用隔离法。
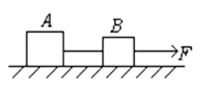
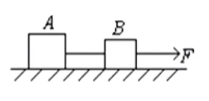
模型一
如图所示,已知 m A , m B , F T a
首先判断两物体加速度是否相同。一般有两种判断方法:
题目中有「一起」或「共同」运动之类的字眼。
分类讨论两个物体之间的加速度的大小关系(大于、小于和等于)。
此题考虑分类讨论:
当 a A > a B v A v B A
当 a A < a B v B v A
综上所述,一定有 a A = a B
对 A , B
{ ( m A + m B ) a = F F 支 = ( m A + m B ) g ⟹ a = m A + m B F
由于 A A
{ m A a = T F 支 = m A g ⟹ T = m A a = m A + m B m A F
模型二
如图所示,已知 m A , m B , F T a
同理可知 a A = a B A , B
( m A + m B ) a = F − ( m A + m B ) g ⟹ a = m A + m B F − g
注意加速度的表达式尽量化到最简。
对 B
m B a = T − m B g ⟹ T = m A + m B m B F
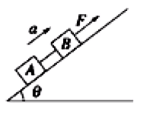
模型三
如图所示,已知 m A , m B , F , θ T a
对 A , B
{ ( m A + m B ) a = F − ( m A + m B ) g sin θ F N = ( m A + m B ) g ⟹ a = m A + m B F − g sin θ
对 A
{ m A a = T − m A g sin θ F N = m A g cos θ ⟹ T = m A + m B m A F
模型四
如图所示,已知 m A , m B , F T a
对 A , B
{ ( m A + m B ) a = F − μ F N F N = ( m A + m B ) g ⟹ a = m A + m B F − μ g
对 A
{ m A a = T − μ F N F N = m A g ⟹ T = m A + m B m A F
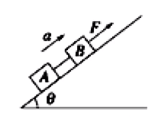
模型五
如图所示,已知 m A , m B , F , θ T a
对 A , B
{ ( m A + m B ) a = F − μ F N − ( m A + m B ) g sin θ F N = ( m A + m B ) g cos θ ⟹ a = m A + m B F − g sin θ − μ g cos θ
对 A
{ m A a = T − m A g sin θ − μ F N F N = m A g cos θ ⟹ F = m A + m B m A F
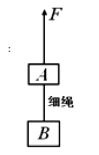
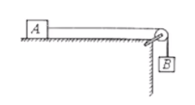
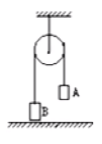
模型六
如图所示,已知 m A , m B B T a
由于此时 a A a B ,故采用隔离法。
对 A
m A a = T ( 1 )
对 B
m B a = m B g − T ( 2 )
( 1 ) + ( 2 )
a = m A + m B m B g
代入 ( 1 )
T = m A + m B m A m B g
模型七
如图所示,已知 m A , m B A T a
此时 a A a B
对 A
m A a = m A g − T ( 1 )
对 B
m B a = T − m B g ( 2 )
( 1 ) + ( 2 )
a = m A + m B m A g − m B g
代入 ( 2 )
T = m A + m B 2 m B m A g
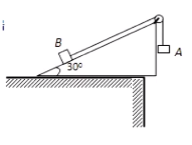
模型八
如图所示,已知 m A , m B A T a
对 B
m B a = T − m B g sin θ ( 1 )
对 A
m A a = m A g − T ( 2 )
( 1 ) + ( 2 )
a = m A + m B m A g − m B g sin θ
代入 ( 2 )
T = m A + m B m A m B g + m A m B g sin θ
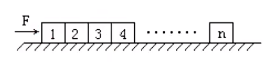
例题
如图所示,n m F 1 3 4
分析:
发现 1 ∼ n
a = nm F
由于求的是木块 3 4 4 ∼ n
( n − 3 ) ma = N ⟹ N = n ( n − 3 ) F
技巧&总结:当物体的数量较多时,可以考虑隔离其中一部分物体作为整体利用整体法求解。
【模型】多物体弹簧突变
解题方法
计算弹簧弹力;
把弹簧弹力看成外力,重新受力分析。
一般情况下,受力分析中只有「外力」和「重力」可以直接明确算出大小,其他均需要通过受力分析求出。
例题
如图所示,吊篮 A B C m , 3 m , 2 m B C B C
A. 吊篮 A g
B. 物体 B g
C. 物体 C 2 g
D. A 、 B 、 C g
分析:
对 B F N = 3 mg
将弹簧弹力当成外力,再对装置各个部分受力分析。
首先以 B
m B a = m B g − F N ⟹ a = 0
对 C A F 支 A F 支 A , C
分类讨论 a A a C
若 a A > a C v A > v C A C A g C 2.5 g a A > a C
若 a A < a C v A < v C C A
所以 a A = a C
对 A , C
3 ma = 6 m g ⟹ a = 2 g
故选 C。
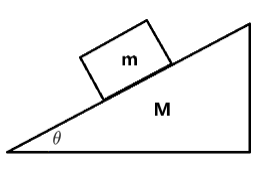
【模型】叠加体
与连接体的区别:连接体是靠弹力连接物体,叠加体靠摩擦力连接物体。
推导
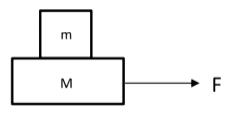
模型一
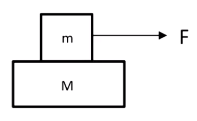
如图所示,已知 m , M , F m
由于两物体相对静止,所以他们之间的摩擦力是静摩擦力,同时两物体加速度相同,可利用整体法。
对两物体整体受力分析:
( m + M ) a = F ⟹ a = m + M F
由于 m m
ma = f ⟹ f = m + M m F
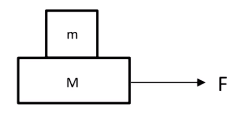
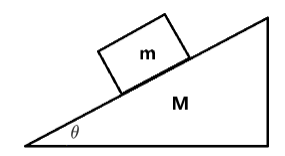
模型二
如图所示,已知 m , M , F m
对两物体整体受力分析:
( m + M ) a = F ⟹ a = m + M F
对 M
M a = f ⟹ m + M M F
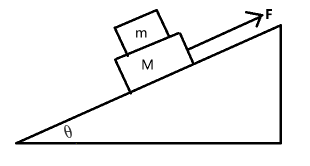
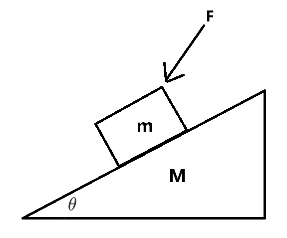
模型三
如图所示,已知 m , M , F m
对两物体整体受力分析:
( m + M ) a = F − ( m + M ) g sin θ ⟹ a = m + M F − g sin θ
对 m
ma = f − m g sin θ ⟹ f = m + M m F
模型四
如图所示,已知 m , M , F m
对两物体整体受力分析:
( m + M ) a = F − μ ( m + M ) g ⟹ a = m + M F − μ g
对 m
ma = f ⟹ f = m + M m F − μ m g
叠加体相对滑动临界问题
解题思路
找到不受外力 的物体。
通过隔离法求出 1 中物体的最大加速度 a
整体法求外力 F
例题
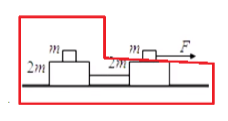
如图所示,光滑水面上放置质量分别为 m 2 m 2 m 2 μ m g F m 2 m
分析:
当 F F m 2 m
由于题目中涉及两对木块会产生摩擦力,所以需要分类讨论哪一对先达到最大摩擦力 2 μ m g 2 μ m g F F
若左边这对木块间的摩擦力是 2 μ m g m
ma = 2 μ m g ⟹ a = 2 μ g
对整个装置整体受力分析:
6 ma = F ⟹ F = 12 μ m g
若右边这对木块间的摩擦力是 2 μ m g 2 m a F T
如图所示,考虑将红框部分作为一个整体受力分析:
5 ma = 2 μ g ⟹ a = 5 2 μ g
对整个装置作为整体受力分析:
6 ma = F ⟹ F = 5 12 μ g
由于 5 12 μ m g < 12 μ m g 2 μ m g
对右边下方质量为 2 m
2 ma = f m a x − T ⟹ T = f m a x − 2 ma = 5 6 μ m g
另解:
根据连接体的推导可知,如果我们将上图中整个红框 看作一个整体,那么相当于红框部分不受外力,非红框部分受到向右的外力 F f 1
f 1 = 6 5 F
同时将两边两个叠加木块分别看作一个整体,相当于左边两个木块叠加整体不受外力,令绳子拉力为 T
T = 2 1 F
再将下图红框部分作为一个整体。
令红框部分与非红框部分是 f 2
f 2 = 6 1 F
由于木块间最大摩擦力 f m a x 2 μ m g F f 1 f m a x
考虑计算此时的最大拉力 T
T = 2 1 F = 2 1 × 5 6 f 1 = 5 3 f m a x = 5 6 μ m g
技巧&总结:
要善用整体思想,例如:求上图左侧两物体之间的摩擦力,考虑将红框作为一个整体看待;求绳子拉力 T
【模型】等时圆
基本思想
设物理量:
一般要设题目给定的「不变量」,例如下面的模型一,斜面高相同(不变),所以设高度;模型二,斜面底相同(不变),所以设底面长度。
遇到圆要设半径 R
一般还需要设斜面倾斜角度 θ
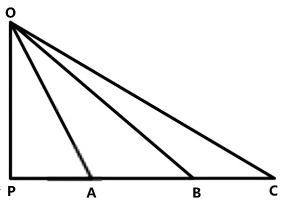
模型一
如图所示,一小球从点 O O A , OB , OC A , B , C O A , B , C
设斜面与水平面的夹角为 θ OP = H a = g sin θ v 0 = 0
根据运动学公式 2 a x = v t 2 − v 0 2
2 ⋅ g sin θ ⋅ sin θ H = v t 2 − 0 ⟹ v t = 2 g H
所以小球从三个斜面上滑下末速度相同。
又由于 t = a Δ v = g sin θ v t θ t O A
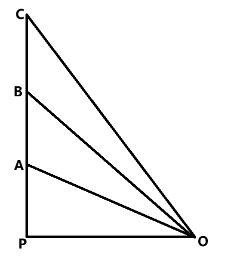
模型二
如图所示,一小球分别从 A , B , C A O , BO , CO O
设斜面与水平面的夹角为 θ OP = L a = g sin θ v 0 = 0
根据运动学公式 x = 2 1 a t 2
cos θ L = 2 1 g sin θ ⋅ t 2 ⟹ t = g sin θ cos θ 2 L = g sin 2 θ 4 L
当 θ ∈ [ 0 ∘ , 9 0 ∘ ] 2 θ ∈ [ 0 ∘ , 18 0 ∘ ] sin 2 θ [ 0 ∘ , 4 5 ∘ ] ( 4 5 ∘ , 9 0 ∘ ] t [ 0 ∘ , 4 5 ∘ ] ( 4 5 ∘ , 9 0 ∘ ] 3 0 ∘ , 4 5 ∘ , 6 0 ∘ 3 0 ∘ 60 X ∘ 4 5 ∘
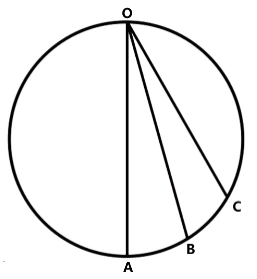
模型三
如图所示,在该圆的最高点 O O A , OB , OC A , B , C
设圆的半径为 R O A θ a = g cos θ v 0 = 0
根据直径所对圆周角是直角,可得斜面长度 x = 2 R cos θ x = 2 1 a t 2
2 R cos θ = 2 1 g cos θ ⋅ t 2 ⟹ t = g 4 R
所以时间 t R A , B , C
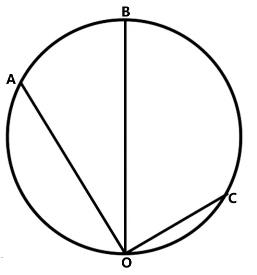
模型四
如图所示,在该圆的 A , B , C A O , BO , CO O
设圆的半径为 R OB θ a = g cos θ v 0 = 0
根据直径所对圆周角是直角,可得斜面长度 x = 2 R cos θ x = 2 1 a t 2
2 R cos θ = 2 1 g cos θ ⋅ t 2 ⟹ t = g 4 R
所以时间 t R O
注意:等时圆必须保证起点或终点在圆上最高点或最低点 。
【模型】斜面滑块
基本思路&步骤与多物体牛二的解题思路相同。
注意:
计算斜面滑块问题时,如果题目未说明物块的运动状态,需要先判断物块是静止还是运动。(见下方例题)
对于受力分析时摩擦力方向不能直接确定时,可以考虑假设一个方向,然后求出摩擦力,根据求出的正负判断。
例题
如图所示,已知木块质量 m = 1 kg M = 3 kg θ = 3 7 ∘ μ = 0.5 m M M
由于题目未告诉 m M
对 m G x = m g sin θ f m a x = μ m g cos θ G x > f m a x m
对 m
F N = m g cos θ
对 M M f
μ F N cos θ = F N sin θ + f ⟹ f = μ m g cos 2 θ − m g cos θ sin θ = m g cos θ ( μ cos θ − sin θ )
由于 μ cos θ − sin θ < 0 f f = m g cos θ sin θ − μ m g cos 2 θ
判断摩擦力方向
方法技巧
当受力分析时不能确定某个力的方向(一般是摩擦力 f
例题
例 1:如图所示,木块在斜面上,斜面(粗糙)始终静止。求以下情况地面对 M
木块在斜面上恰好可以匀速下滑。
木块在斜面上加速下滑。
木块在斜面上减速下滑。
分析:
当木块在斜面上可以匀速下滑时:
对木块 m F N M f F m g F M
再对斜面 M m M F ′ F M M M
当木块在斜面上加速下滑时:
对木块 m F N M F F
再对斜面 M M m F ′ x M f
同理可知,当木块在斜面上减速下滑时:f
例 2:如图所示,木块在斜面上匀速下滑,斜面(粗糙)始终静止。则在此方向上对木块 m F M
首先考虑施加外力前,根据上题第一种情况的分析可知,m M M
施加外力 F F N f = μ F N f F N m M M M
通过上面两道例题可以看出:
当斜面粗糙程度不变(即例 1 的第一种情况和例 2)只改变外力时,不会影响地面对 M
只有粗糙程度改变(例 1 的三种情况),才会影响地面对 M
【模型】传送带
求解步骤
受力分析:先对初始状态 下的物体进行受力分析,再对与传送带共速 时的物体进行受力分析(因为共速时的摩擦力的性质可能会发生变化)。
根据受力分析列式子求加速度。
根据所求加速度画出 v − t
根据图象求解问题。
注意:
在计算共速时摩擦力 时,需要计算比较最大静摩擦力(滑动摩擦力)与 G x
对于解答题,v − t
对于判断传送到从某地到某地时间的问题,一般可以通过初始状态时的受力分析和 v − t
相对位移
物体相对传送带的位移计算公式为:
x 相 = x 物 − x 传
一般物体的位移 x 物 x 传 = v t
划痕
问题模型:一煤块被放上传送带,经过某段距离后,离开传送带,问其对传送带的划痕是多少。
一般有两种情况。
情况一——单方向位移
物体始终相对于传送带只进行了「一段位移」,即物体相对于传送带只发生了一次单方向位移。
一般情况下是物体初始时速度 v 物 < v 0 v 物 = v 0
求解:实际上划痕可以转化为物块相对于传送带的位移大小 ,即 ∣ x 相 ∣
那么有:
∣ x 相 ∣ = ∣ x 物 − x 传 ∣
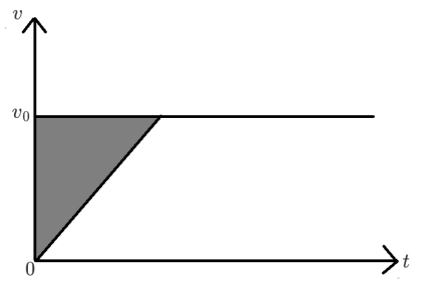
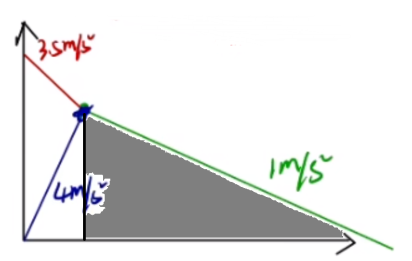
在 v − t v 0 0
则划痕表示为图中灰色阴影部分面积。
情况二——多方向位移
物体相对于传送带进行了「多段位移」,即物体相对于传送带多次在不同方向发生位移。
一般情况下是物体初速度 v 物 < v 0 v 物 > v 0
求解:此时划痕为多段位移 x 1 , x 2 , ⋯ ∣ x m a x ∣
最短通过时间
问题模型:将一物体放在传送带的起点,问:如果物体想要以最短时间 由起点到终点,则传送带至少 要多大的速度传送。
第一段运动:物体从初速度为 0 a a
第二段运动:当物体的速度与传送带相同时,物体要么与传送带保持共速,要么做加速度 <
要使得物体通过传送带的时间最短,则须保证「第一段运动」尽可能长,又要传送带速度最小,则 v m i n = 2 a x a x
物体末速度
注:此类型的题目一般在选择题中出现。
问题模型:物体以一初速度 v 0 v 传
这里以水平传送带为例 。
求解:
当 v 0 = v 传
当 v 0 < v 传 a 2 a x = v t 2 − v 0 2 v t
分析可知:当 v t ≤ v 传 v t v t > v 传 v 传 v 传 v 传
当 v 0 > v 传 a v t
分析可知:当 v t ≥ v 传 v t v t < v 传 v 传 v 传 v 传
【模型】板块模型
分类
板块模型的题目:
按照有无外力分为「有外力」和「无外力」两种类型,其中「无外力」情况中一般物体会有初速度。
按照粗糙/光滑分为「地面光滑」、「地面粗糙 + μ 地 < μ 滑 + μ 地 > μ 滑
做题思路
工具:
受力分析:「初始状态」、「共速状态」和「突发状态」三种情况需要受力分析。
图象:v − t x 负 的。
方法:钩子法(先整体后隔离)。
适用范围:共速且不受外力。
内容:
首先假设滑块木板能够一起向右运动,则对整体受力分析,可知 a 1 = μ 地 g a 2 = μ 滑 g a 2 a 1
此时有两种情况:
当 a 2 < a 1 μ 滑 < μ 地 隔离法 。
当 a 2 > a 1 μ 滑 > μ 地 整体法 。
无外力 +
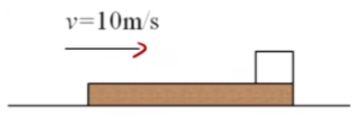
如图所示,一足够长的木板在水平地面上滑动,速度 v = 10 m / s m = 1 kg M = 2 kg μ 1 = 0.4 g 10 m / s 2
经过多长时间物块相对木块停止运动?
木块相对于木板的位移是多少米?
分析:
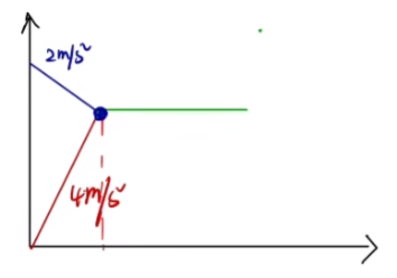
初始状态,考虑先对物块受力分析可得物块的加速度 a 1 = μ 1 g = 4 m / s 2 a 2 = M μ 1 m g = 2 m / s 2 v − t
所以在交点对应位置,两者共速(即物块相对木板停止运动)。
设物块初速度为 v 0 v 1
v 物 = v 木 ⟹ v 0 + a 1 t = v 1 + a 2 t ⟹ t = 3 5 s
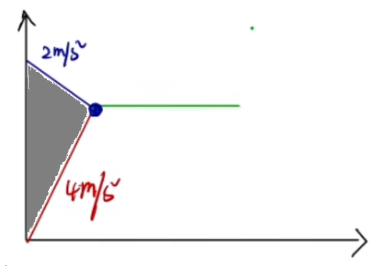
木块相对于木板的位移
x 相 = x 物 − x 木
在 v − t
此时 x 相 = 2 1 × 3 5 × 10 = 3 25 m
无外力 +
μ 地 < μ 滑 如图所示,一足够长的木板在水平地面上滑动,速度 v = 10 m / s m = 1 kg M = 2 kg μ 1 = 0.4 μ 2 = 0.1 g 10 m / s 2
木板和物块相对静止后还能向前滑行的距离是多少?
整个过程中木板的位移、物块的位移和木块相对木板的位移分别是多大?
分析:
初始状态,先对物块受力分析得物块加速度 a 1 = μ 1 g = 4 m / s 2 a 2 = M μ 1 m g + μ 2 ( M g + m g ) = 3.5 m / s 2
两者共速时,不受外力,所以考虑使用「钩子法」,由于此时 μ 1 > μ 2 a = 1 m / s 2 v − t
设物块初速度为 v 0 v 1
v 物 = v 木 ⟹ v 0 + a 1 t = v 1 + a 2 t ⟹ t = 3 4 s
所以可求出交点处两者速度为 v = a 1 t = 3 16 m / s
那么两者相对静止后向前滑动的时间 t = a v = 3 16 s
所以位移 x = 2 1 × 3 16 × 3 16 = 9 128 m
物体运动的位移就是下方阴影部分面积:
所以 x 物 = 2 1 × 3 20 × 3 16 = 9 160 m
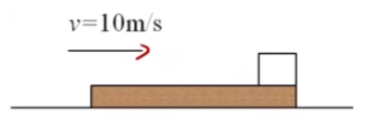
μ 地 > μ 滑 如图所示,一足够长的木板在水平地面上滑动,速度 v = 10 m / s m = 1 kg M = 2 kg μ 1 = 0.4 μ 2 = 0.6 g 10 m / s 2
物块与木板何时共速?
物块、木板和物块相对木板的位移是多大?
要使得物块全程不滑出木板,木板最少要多长?
物块对木板的划痕有多长。
分析:
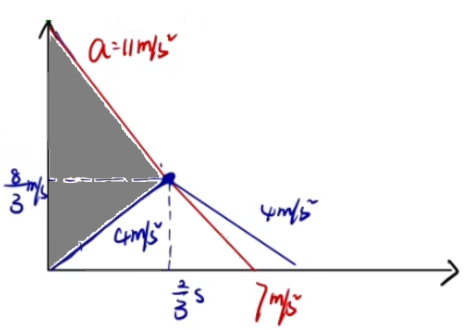
初始状态,先对物块受力分析得物块加速度 a 1 = 4 m / s 2 a 2 = 11 m / s 2
此时两者共速,且不受外力,考虑「钩子法」,由于 μ 1 < μ 2
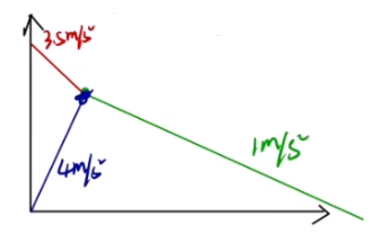
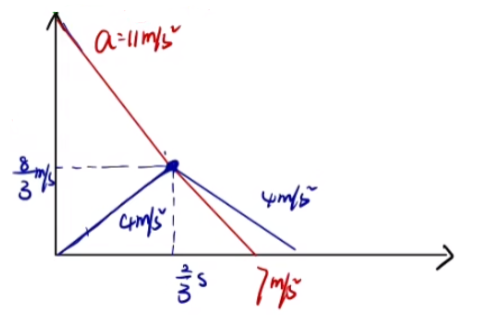
首先对共速时得物块受力分析,此时物块为了与木板保持共速(即一起向右做加速度减小的减速运动,加速度向左),会受到木板对它向左的摩擦力 ,得物块加速度 a 3 = 4 m / s 2 a 1 相反 。再对共速时的木板受力分析,求得木板此时的加速度 a 4 = 7 m / s 2
设物块初速度为 v 0 v 1
v 物 = v 木 ⟹ v 0 + a 1 t = v 1 + a 2 t ⟹ t = 3 2 s
绘制 v − t
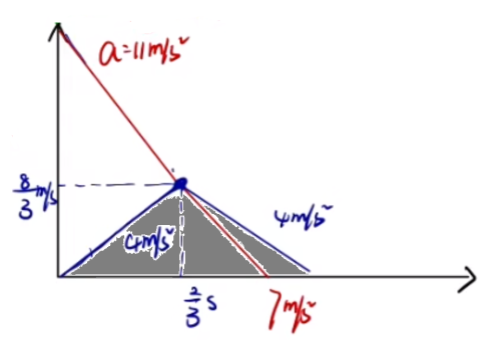
那么此时木块的位移用下图阴影部分表示:
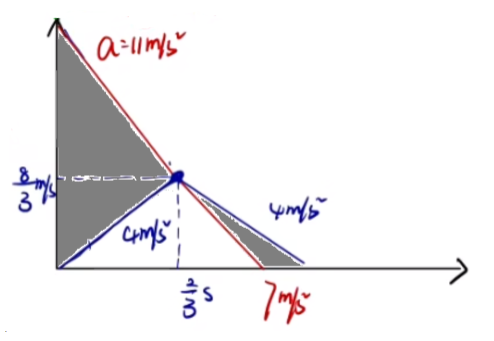
所以 x 物 = 2 1 × 3 8 × 3 4 = 9 16 m x 木
那么物块相对木板的位移就是 x 物 − x 木
起初物块的速度 < >
所以木板最短长度应该为下图阴影面积:
划痕则为下图两部分阴影面积中较大的一块:
有外力
做题思路
首先求出外力 F F m a x
具体:
找到加速度 a
将其隔离进行受力分析。
求出它的加速度 a
对整体受力分析求出 F m a x
那么若实际外力 F > F m a x F ≤ F m a x
例题
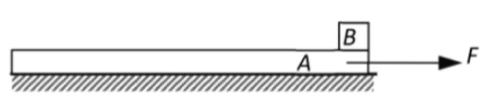
如图所示,光滑水平面上静止放着长 L = 1.6 m M = 3 kg m = 1 kg m M μ = 0.1 F g 10 m / s 2 F = 10 N F
由于 B B a = 1 m / s 2 A B F m a x = 4 N
由于 F = 10 N > 4 N A B a B = 1 m / s 2 A a A = M F − μ m g = 3 m / s 2
随着时间增大,v A > v B A B B A F v B v A v B A B F A a a B ′ = 3 1 m / s 2 A B
两物体共速时,不受外力。所以考虑使用「钩子法」,由于下表面光滑,下表面粗糙,所以二者能够保持共速一起运动。整体法对 A B
绘制 v − t
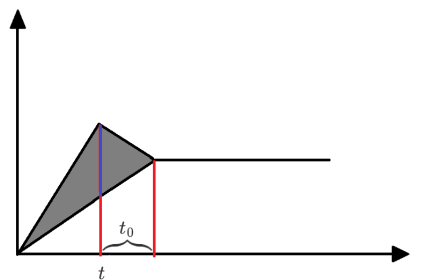
要使得小物块恰好从木板上滑下,则图中阴影部分面积应该为 1.6 m F t
当时间为 t B t m / s A 3 t m / s 2 t m / s 2 t A B t 0
t + t 0 = 3 t − 3 1 t 0 ⟹ t 0 = 1.5 t
那么有
S △ 左 + S △ 右 = 2 1 ⋅ 2 t ⋅ t + 2 1 ⋅ 2 t ⋅ 2 3 t ⟹ t = 0.8 s








【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!