【文化课学习笔记】【化学】选必一：水溶液中的离子反应与平衡（下）

【化学】选必一：水溶液中的离子反应与平衡（下）

盐类水解

基本概念

定义：盐电离出的离子与水电离出的 $\ce{H+}$ 或 $\ce{OH-}$ 相互作用生成弱电解质的反应。
特点：
- 可逆：水解是可逆反应，在一定条件下达到化学平衡。
- 程度小：通常盐类水解程度很小，一般无沉淀析出、无气体放出。例如 $\ce{Al^3+}$ 水解方程式为 $\ce{Al^3+ + 3H2O <=> Al(OH)3 + 3H+}$ 这里的 $\ce{Al(OH)3}$ 不能标上沉淀符号，因为水解没有沉淀析出。同理，铵根水解不能得到氨气。
- 吸热：盐类水解实际上是酸碱中和反应的逆反应，为吸热反应。温度升高，水解程度增大。
规律性：

【正盐】

有弱才水解，无弱不水解。注意：强酸强碱不存在水解，也不会影响水溶液的酸碱性。
- 强酸弱碱盐：盐电离的阳离子与溶液中的 $\ce{OH-}$ 结合生成弱碱，溶液呈酸性，如 $\ce{NH4Cl、CuSO4}$ 溶液。
- 强碱弱酸盐：盐电离的阴离子与溶液中的 $\ce{H+}$ 结合生成弱酸，溶液呈碱性，如 $\ce{Na2S、Na2CO3}$ 溶液。
- 强酸强碱盐：盐电离产生的阴阳离子都不能与溶液中的 $\ce{H+}$ 或 $\ce{OH-}$ 结合生成弱电解质，不发生水解，溶液呈中性，如 $\ce{NaCl、KNO3}$ 溶液。
概括：正盐水溶液的酸碱性，谁强显谁性。

酸强碱弱显酸性

碱强酸弱显碱性

两者皆强显中性

两者皆弱不一定（谁的水解程度大显谁性）

【弱酸的酸式盐】

弱酸的酸式酸根既能水解又能电离，其钠盐所形成的水溶液酸碱性，取决于其水解和电离程度的相对大小。
- 电离程度 $>$ 水解程度，溶液呈酸性。例如：$\ce{NaHSO3、NaH2PO4、NaHC2O4}$ 等。
- 电离程度 $<$ 水解程度，溶液呈碱性。例如：$\ce{NaHCO3、NaHS、Na2HPO4}$ 等。
- $\ce{CH3COO-}$ 与 $\ce{NH4+}$ 二者的水解程度基本相等，溶液几乎呈中性。
弱酸根阴离子所对应的酸越弱，则其水解程度越大。原因：酸性越弱，越不易电离，反而越容易和氢离子结合，水解程度就越大。

弱酸酸性顺序/电离程度/$K_a$：

\[\ce{CH3COOH > H2CO3 > HClO > HCO3- > Al(OH)3} \]
弱酸根碱性顺序/水解程度/$\ce{pH}$ 值/$K_h$/与氢离子结合能力：

\[\ce{CH3COO- < HCO3- < ClO- < CO3^2- < AlO2-} \]
其中 $K_h$ 表示水解平衡常数。

同温度、同浓度下的 $\ce{CH3COONa、NaHCO3、NaClO、Na2CO3、NaAlO2}$ 五种溶液，其 $\ce{pH}$ 大小为：

\[\ce{CH3COONa < NaHCO3 < NaClO < NaAlO2} \]
同温度、同 $\ce{pH}$ 值的上述五种溶液，溶液中的 $c(\ce{Na+})$ 大小为：

\[\ce{CH3COONa > NaHCO3 > NaClO > NaAlO2} \]
【双水解】

都弱双水解，有些「完全」双水解。

一种盐的阳离子与另一种盐的阴离子都发生水解，两者混合时，两种离子均发生水解，即双水解。

若两种离子水解趋于完全（完全双水解/彻底双水解/强烈双水解），此时用 "$=$" 连接反应物和生成物，水解生成的难溶物和气体后应标示沉淀符号 $\ce{v}$ 和气体符号 $\ce{^}$。

例如：$\ce{Al3+}$ 与 $\ce{HCO^3-}$ 混合于同一水溶液中，前者水解生成的氢离子与后者水解生成的氢氧根离子不断结合生成水，从而根据同离子效应，两者不断水解，最后达到彻底双水解，生成 $\ce{Al(OH)3}$ 沉淀和 $\ce{CO2}$ 气体。

常见的彻底双水解

\[\begin{aligned}{} &\ce{Al^3+ : CO3^2-、HCO3- 、S^2-、HS- 、AlO2^-、ClO-}\\ &\ce{Fe^3+ : CO3^2-、HCO3- 、AlO2- 、ClO-}\\ &\ce{NH4+ : SiO3^2-、AlO2-} \end{aligned} \]

注意：$\ce{NH4+}$ 遇到 $\ce{HCO3- 、CO3^2-、CH3COO-}$ 等离子，水解会相互促进，但反应扔不完全，应用 $\ce{<=>}$ 连接。

盐类水解的影响因素

内因（决定因素）

盐类水解程度的大小主要由盐的性质决定，对于强碱弱酸盐来说，生成盐的弱酸酸性越弱，越难电离（$K_a$ 越小），该盐的水解程度越大，碱性就越强，即越弱越水解。

同理，对于强酸弱碱盐来说，生成盐的弱碱碱性越弱，酸性越强，该盐水解程度越大。

例如，同温下，相同浓度的 $\ce{NH4Cl}$ 溶液与 $\ce{AlCl3}$ 溶液，由于生成 $\ce{NH4Cl}$ 的弱碱 $\ce{NH3.H2O}$ 的电离程度大于生成 $\ce{AlCl3}$ 的两性氢氧化物 $\ce{Al(OH)3}$（由于是两性，所以碱性极弱），即 $\ce{Al(OH)3}$ 的碱性更弱，所以对应的 $\ce{AlCl3}$ 的水解程度就越大，所以 $\ce{AlCl3}$ 溶液的酸性也更强。

注意：若在常温下，某正盐溶液 $\ce{NaX}$ 的 $\ce{pH = 7}$，则说明 $\ce{HX}$ 是强酸。

外因

温度：盐类水解可看做酸碱中和反应的逆反应，是吸热反应，因此加热可促使平衡向水解反应的方向移动，盐的水解程度增大，即越热越水解。
浓度：
- 加水（减小盐浓度）：水解程度增大，即越稀越水解。
- 加溶质（增大盐浓度）：水解程度减小。
加酸/碱：
- 对强碱弱酸盐，加酸促进水解，加碱抑制水解：强碱弱酸盐水解生成酸和 $\ce{OH-}$，加碱增大 $\ce{OH-}$，根据同离子效应，抑制水解；加酸减小 $\ce{OH-}$，促进水解。
- 对强酸弱碱盐，加酸抑制水解，加碱促进水解：理由同理。
总结：酸可抑制阳离子水解，促进阴离子水解；碱可抑制阴离子水解，促进阳离子水解。

记忆：同性抑制，异性促进。
加盐：
- 水解情况相同的离子的水解相互抑制：例如，氯化铁水溶液中加入氯化镁固体，两者都会水解产生弱碱和 $\ce{H+}$，这样对方产生的 $\ce{H+}$ 就会因为同离子效应对自己的水解产生抑制。
- 水解情况相反的离子的水解相互促进（双水解）：道理同上。
总结：酸性盐抑制酸性盐水解，促进碱性盐水解；碱性盐抑制碱性盐水解，促进酸性盐水解。

记忆：同性抑制，异性促进。

应用

在 $\pu{0.01 mol*L-1}$ 的 $\ce{FeCl3}$ 溶液中，存在水解平衡：

\[\ce{Fe^3+ + 3H2O <=> Fe(OH)3 + 3H+} \]

那么：

改变条件	平衡移动	水解程度	$c(\ce{H+})$	$\ce{pH}$	现象
升高温度	正向移动	增大	增大	降低	颜色变深
加水稀释	正向移动	增大	减小	升高	颜色变浅
加 $\ce{FeCl3}$ 固体	正向移动	减小	增大	降低	颜色变深
加 $\ce{HCl}$	逆向移动	减小	增大	降低	颜色变浅
加 $\ce{NaOH}$	正向移动	增大	减小	升高	红褐色沉淀
加 $\ce{CaCO3}$ 固体	正向移动	增大	减小	升高	红褐色沉淀+无色气体
加 $\ce{NH4Cl}$	逆向移动	减小	增大	降低	颜色变浅
加 $\ce{NaF}$	正向移动	增大	减小	升高	颜色变深
加 $\ce{NaHCO3}$	正向移动	增大	减小	升高	红褐色沉淀+无色气体

说明：

加水稀释由于体积膨胀，虽然平衡正向移动，$n(\ce{H+})$ 增大，但平衡正向移动无法抵消氢离子浓度的降低，$c(\ce{H+})$ 反而降低。或者也可以理解为氯化铁溶液本身显酸性，加水稀释使得酸被稀释，即 $c(\ce{H+})$ 降低。

也可以理解为加水稀释使得能够促进水电离的 $\ce{FeCl3}$ 浓度降低，从而使得水的电离相比之前减弱，降低了溶液中的 $c(\ce{H+})$。
加入 $\ce{FeCl3}$ 固体后，平衡正向移动，但水解程度反而降低，因为第二次加入的氯化铁由于第一次加入氯化铁水解产生的影响，第二次的水解程度反而小于第一次。
加入 $\ce{FeCl3}$ 固体后，由于平衡正向移动，所以 $n(\ce{H+})$ 增大，体积可视为不变，所以 $c(\ce{H+})$ 增大。
加入 $\ce{NaOH}$ 固体后，平衡正向移动，使得氯化铁水解程度增大，当 $\ce{NaOH}$ 足够多时，就会产生红褐色沉淀 $\ce{Fe(OH)3}$。
加入 $\ce{CaCO3}$ 固体后，会与 $\ce{H+}$ 生成气体 $\ce{CO2}$，所以降低溶液中的 $c(\ce{H+})$，根据同离子效应，平衡正向移动。当 $\ce{CaCO3}$ 足够多时，就会产生红褐色沉淀 $\ce{Fe(OH)3}$。
加入 $\ce{NH4Cl}$ 后，由于 $\ce{NH4+}$ 水解产生 $\ce{H+}$，根据同离子效应，平衡逆向移动，所以 $c(\ce{H+})$ 增大。
加入 $\ce{NaF}$ 后，由于 $\ce{F-}$ 水解产生 $\ce{OH-}$，消耗 $\ce{H+}$，所以 $c(\ce{H+})$ 减小，根据同离子效应，平衡正向移动。同时 $\ce{F-}$ 与 $\ce{Fe^3+}$ 的水解为双水解。
加入 $\ce{NaHCO3}$ 后，由于 $\ce{HCO3-}$ 水解产生 $\ce{OH-}$，会与 $\ce{Fe^3+}$ 的水解形成完全双水解，从而导致平衡正向移动，水解程度增大。 $\ce{H+}$ 被 $\ce{OH-}$ 中和，所以 $c(\ce{H+})$ 减小，$\ce{pH}$ 升高。由于完全双水解，反应生成红褐色沉淀 $\ce{Fe(OH)3}$ 和无色气体 $\ce{CO2}$。

电解质溶液三大守恒

电荷守恒

书写法则：阳离子摆一边，阴离子摆一边，电荷数往前乘。

例：

$\ce{Na2CO3}$ 溶液：

\[c(\ce{Na+}) + c(\ce{H+}) = 2c(\ce{CO3^2-}) + c(\ce{HCO3-}) + c(\ce{OH-}) \]

$\ce{NaHCO3}$ 溶液：同上。

$\ce{Na2CO3}$ 溶液与 $\ce{NaHCO3}$ 溶液按照体积比 $2:1$ 混合：同上。

$\ce{K3PO4}$ 溶液：

\[c(\ce{K+}) +c(\ce{H+}) = 3c(\ce{PO4^3-}) + 2c(\ce{HPO4^2-}) + c(\ce{H2PO4-}) + c(\ce{OH-}) \]

$\ce{NH3}$ 通入 $\ce{NaHSO3}$ 溶液：

\[c(\ce{Na+}) + c(\ce{NH4+}) + c(\ce{H+}) = c(\ce{HSO3-}) + 2c(\ce{SO3^2-}) + c(\ce{OH-}) \]

物料守恒（元素守恒）

关键：找准“变化前”的核心元素之间的比例，以及核心元素在水溶液中的所有存在状态。

注意：这里的「核心元素」不包含 $\ce{H+}$ 和 $\ce{OH-}$。

例：

$\ce{Na2CO3}$ 溶液：由于投料时 $\ce{Na :CO3^2-} = 2:1$，所以有：

\[c(\ce{Na+}) = [c(\ce{CO3^2-}) + c(\ce{HCO3-}) +c(\ce{H2CO3})]\times 2 \]

$\ce{NaHCO3}$ 溶液：由于投料时 $\ce{Na :HCO3-} = 1:1$，所以有：

\[c(\ce{Na+}) = c(\ce{CO3^2-}) + c(\ce{HCO3-}) +c(\ce{H2CO3}) \]

向 $\pu{20 mL}\ \pu{0.1mol*L-1}\ \ce{CH3COOH}$ 溶液中逐滴加入 $\pu{0.1mol*L-1}\ \ce{NaOH}$ 溶液，如图：

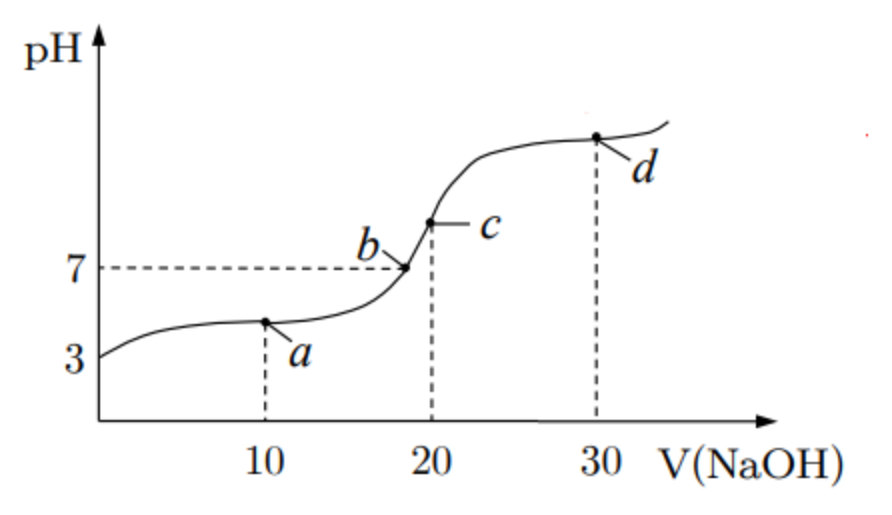
对于 $a$ 点，$\ce{NaOH:CH3COOH = 1:2}$ 投料，相当于恰好中和一半，即溶液中含有等量的弱酸及其盐，此时有：

\[2c(\ce{Na+}) = c(\ce{CH3COOH}) + c(\ce{CH3COO-}) \]
对于 $c$ 点，$\ce{NaOH:CH3COOH} = 1:1$ 投料，相当于恰好完全中和，此时溶液是一杯醋酸钠水溶液，有：

\[c(\ce{Na+}) = c(\ce{CH3COOH}) + c(\ce{CH3COO-}) \]
对于 $d$ 点，$\ce{NaOH:CH3COOH} = 3:2$ 投料，此时有：

\[2c(\ce{Na+}) = [c(\ce{CH3COOH}) + c(\ce{CH3COO-})]\times 3 \]

质子守恒

含义：由水电离出来的 $\ce{H+}$ 必等于水电离出的 $\ce{OH-}$，即溶液中所有物质得到的 $\ce{H+}$ 等于失去的 $\ce{OH-}$。

注意：水电离出的 $\ce{H+}$ 不一定就以单个 $\ce{H+}$ 的“身份”存在于溶液中。例如 $\ce{Na2CO3}$ 溶液中的 $\ce{H+}$ 可能跟 $\ce{CO3^2-}$ 结合形成 $\ce{HCO3-}$。

单一盐溶液

表格法，关键是要弄清水电离出来的氢离子或氢氧根离子被谁得到。

例：

注：表格中的核心物质是可能发生水解或电离的物质，即可能得到 $\ce{H+}$ 也可能失去 $\ce{H+}$ 的物质。

$\ce{Na2CO3}$ 溶液：

得到 $\ce{H+}$	核心物质	失去 $\ce{H+}$（得到 $\ce{OH-}$）
$\ce{H+}$	$\ce{H2O}$	$\ce{OH-}$
得到一个 $\ce{H+}$：$\ce{HCO3-}$，得到两个 $\ce{H+}$：$\ce{H2CO3}$	$\ce{CO3^2-}$	/

所以质子守恒：

\[c(\ce{H+}) +c(\ce{HCO3-}) +2c(\ce{H2CO3}) = c(\ce{OH-}) \]

$\ce{NaHCO3}$ 溶液：

得到 $\ce{H+}$	核心物质	失去 $\ce{H+}$（得到 $\ce{OH-}$）
$\ce{H+}$	$\ce{H2O}$	$\ce{OH-}$
$\ce{H2CO3}$	$\ce{HCO3-}$	$\ce{CO3^2-}$

所以质子守恒：

\[c(\ce{H+}) + c(\ce{H2CO3}) = c(\ce{OH-}) + c(\ce{CO3^2-}) \]

$\ce{NH4HCO3}$ 溶液：

得到 $\ce{H+}$	核心物质	失去 $\ce{H+}$（得到 $\ce{OH-}$）
$\ce{H+}$	$\ce{H2O}$	$\ce{OH-}$
$\ce{H2CO3}$	$\ce{HCO3-}$	$\ce{CO3^2-}$
/	$\ce{NH4+}$	$\ce{NH3.H2O}$

所以质子守恒：

\[c(\ce{H+}) + c(\ce{H2CO3}) = c(\ce{OH-}) + c(\ce{CO3^2-}) + c(\ce{NH3.H2O}) \]

混合溶液

解题步骤：

判断反应后是否可以变为单一溶液（如完全中和）：例如等浓度、等体积的 $\ce{CH3COOH}$ 和 $\ce{NaOH}$ 混合，则可以变为 $\ce{CH3COONa}$ 水溶液，可直接根据「单一盐溶液」的求解方法表格法进行求解。
写出电荷守恒与物料守恒，消掉不影响水电离的离子（如 $\ce{Na+}$）可得：例如 $\ce{CH3COOH:CH3COONa} = 1:1$，则其电荷守恒和物料守恒分别为：

\[\begin{cases} c(\ce{Na+}) +c(\ce{H+}) = c(\ce{CH3COO-}) +c(\ce{OH-})\\ 2c(\ce{Na+}) = c(\ce{CH3COO-}) +c(\ce{CH3COOH}) \end{cases} \]
联立两式并化简得到质子守恒：

\[c(\ce{CH3COOH}) +2c(\ce{H+}) +c(\ce{CH3COO-}) + 2c(\ce{OH-}) \]
对于两种或多种正盐混合而成的溶液，也可以使用表格法。

例如：$\ce{NH4Cl}$ 和 $\ce{CH3COONa}$ 的混合溶液，有

加 $\ce{H+}$ 核心物质失去 $\ce{H+}$（得到 $\ce{OH-}$

/ $\ce{NH4+}$ $\ce{NH3*H2O}$

$\ce{CH3COOH}$ $\ce{CH3COO-}$ /

$\ce{H+(H3O+)}$ $\ce{H2O}$ $\ce{OH-}$

加 \(\ce{H+}\)	核心物质	失去 \(\ce{H+}\)（得到 \(\ce{OH-}\)
/	\(\ce{NH4+}\)	\(\ce{NH3*H2O}\)
\(\ce{CH3COOH}\)	\(\ce{CH3COO-}\)	/
\(\ce{H+(H3O+)}\)	\(\ce{H2O}\)	\(\ce{OH-}\)

电解质溶液易混淆题型

题型一：等浓度、等体积的酸 + 碱

等浓度、等体积 $\iff$ 等物质的量 $n$。

如果是一元酸 $\ce{HA}$ 与一元碱 $\ce{BOH}$ 等浓度、等体积混合，则酸碱完全中和，得到正盐水溶液，可以直接根据「谁强显谁性」判断 $\ce{pH}$ 的大小。
如果是二元酸 $\ce{H2A}$ 与一元碱 $\ce{BOH}$ 等浓度、等体积混合，会得到酸式盐水溶液，可根据其电离程度与水解程度的大小关系判断 $\ce{pH}$ 的大小。

题型二：常温时 $\ce{pH}$ 之和等于 $14$ 且等体积的酸 + 碱

$\ce{pH} = a~ \iff$ 无论是强酸还是弱酸，一元酸还是二元酸，其溶液中的 $c(\ce{H+})$ 均为 $10^{-a} \ \pu{mol*L-1}$。

强酸和强碱混合，无论是几元酸，由于强酸强碱完全电离，且 $\ce{pH}$ 之和等于 $14$，两种溶液等体积，所以最终得到溶液的 $\ce{pH}$ 均为 $7$，均为中性溶液。
强酸和弱碱混合，弱碱中的「可电离氢离子数目」未完全电离，所以在两种溶液等体积混合后，弱碱仍然会继续电离，即弱碱过量，最终溶液 $\ce{pH > 7}$，为碱性溶液。
弱酸和强碱混合，同理上一条，弱酸过量，最终溶液 $\ce{pH < 7}$，为酸性溶液。

总结：常温时，$\ce{pH}$ 之和等于 $14$ 且等体积的酸碱混合，遵循「谁弱显谁性」。

题型三：溶液呈中性的相关问题

常考题型：

常温下，同浓度、同体积的强酸和强碱溶液混合后，得到的溶液 $\ce{pH}$ 可直接根据题型一的判断方法进行求解。
当温度 $> \pu{25 ^\circ C}$ 时，$\ce{pH}$ 之和等于 $14$ 的强酸强碱溶液等体积混合，由于温度升高，$K_w$ 增大，若强碱溶液的 $\ce{pH} = a$，则对应的 $c(\ce{OH-}) > 10^{-(14-a)}\ \pu{mol*L-1} = c(\ce{H+})$，所以溶液呈碱性。
常温下，若 $V_1\ \pu L\ \ce{pH = 3}$ 的 $\ce{HA}$ 溶液与 $V_2\ \pu{L}\ \ce{pH = 11}$ 的 $\ce{NaOH}$ 溶液混合后显中性，求 $V_1$ 和 $V_2$ 的大小关系。

可以首先分类讨论：

$\ce{HA}$ 是强酸 $\implies$ $V_1 = V_2,\ce{pH = 7}$；

$\ce{HA}$ 是弱酸 $\implies$ 若 $V_1 = V_2$，则溶液显酸性，$\ce{pH < 7}$ $\implies$ 说明弱酸过量 $\implies$ 要使溶液为中性，则 $V_1 < V_2$。

结合上述两点，得 $\ce{V_1 \le V_2}$。
常温下，若 $\ce{pH = 3}$ 的 $\ce{HA}$ 溶液与 $\ce{pH = 11}$ 的 $\ce{NaOH}$ 溶液等体积混合后显中性，则 $c(\ce{A-}) = c(\ce{Na+})$。

理由：根据电荷守恒，有：

\[c(\ce{H+}) + c(\ce{Na+}) = c(\ce{OH-}) + c(\ce{A-}) \]
因为溶液显中性，所以 $c(\ce{OH-}) = c(\ce{H+})$，所以 $c(\ce{Na+}) = c(\ce{A-})$。
常温下，$a\ \pu{mol*L-1}$ 一元酸 $\ce{HA}$ 与 $b\ \pu{mol*L-1}$ 的 $\ce{NaOH}$ 等体积混合后，$\ce{pH =7}$，则 $V_1\ge V_2$。

首先分类讨论：

$\ce{HA}$ 是强酸 $\implies$ $V_1 = V_2$；

$\ce{HA}$ 是弱酸 $\implies$ 若 $V_1 = V_2$，则形成强碱弱酸盐 $\ce{NaA}$，根据「谁强显谁性」，所以 $\ce{pH >7}$ $\implies$ 溶液显碱性，说明 $\ce{NaOH}$ 过量 $\implies$ 要使溶液显中性，则需要增多 $\ce{HA}$，即 $V_1 > V_2$。

结合上述两点，得 $V_1 \ge V_2$。
常温下，$a\ \pu{mol*L-1}$ 一元酸 $\ce{HA}$ 与 $b\ \pu{mol*L-1}\ \ce{NaOH}$ 等体积混合后，$\ce{pH =7}$，则 $c(\ce{A-}) = c(\ce{Na+})$。

理由：同第 4 条。
常温下，$a\ \pu{mol*L-1}$ 一元酸 $\ce{HA}$ 与 $b\ \pu{mol*L-1}\ \ce{NaOH}$ 等体积混合后，$\ce{pH = 7}$，则 $a \ge b$。

理由同理第 5 条。

解题技巧：

题目给定条件有多种解法不同的可能情况时，要善于分类讨论。
先抓「特殊点」随后再进行微调。
中性点比离子浓度，考虑电荷守恒。

题型四：等浓度与等 $\ce{pH}$

水的电离程度解题思路：判断物质促进水电离还是抑制水电离。

抑制水电离：外加酸/碱。其中相同浓度的 $\ce{H+}$ 和 $\ce{OH-}$ 对水电离的抑制效果相同。

促进水电离：加入可水解的盐。
与铝反应生成等量的 $\ce{H2}$，消耗的 $\ce{OH-}$ 比 $\ce{H+}$ 少，所以与足量铝粉反应生成 $\ce{H_2}$ 的量 $\ce{OH-}$ 更多。
等 $\ce{pH}$、等体积的一元强酸、二元强酸和一元弱酸与足量铝粉反应，一元强酸和二元强酸生成 $\ce{H2}$ 的量相同。弱酸生成 $\ce{H2}$ 会更多。（原因详见上文「一元强酸与一元弱酸的比较」）
用等浓度的 $\ce{NaOH}$ 完全中和等 $\ce{pH}$、等体积的一元强酸、二元强酸和一元弱酸，消耗的体积弱酸 $>$ 一元强酸 $=$ 一元弱酸。
等浓度、等体积的一元强酸、二元强酸、一元弱酸、一元强碱和二元强碱与足量铝粉反应，生成 $\ce{H2}$ 的量的顺序为：一元强酸 $=$ 一元弱酸 $<$ 二元强酸 $<$ 一元强碱 $<$ 二元强碱。
用等浓度的 $\ce{NaOH}$ 完全中和等体积的一元强酸、二元强酸、一元弱酸，消耗 $\ce{NaOH}$ 的体积：一元强酸 $=$ 一元弱酸 $<$ 二元强酸。

题型五：盐类水解相关离子比较

解题技巧：讨论各离子对盐类水解的影响。

例如讨论含有铵根离子的盐类中 $c(\ce{NH4+})$ 的大小关系。

规律：

强酸强碱的阴阳离子不影响水解。
加入与所求盐类水解情况相同的离子抑制水解：即使得平衡逆向移动，反而增大 $c(\ce{NH4+})$。
加入与所求盐类水解情况相反的离子促进水解：即使得平衡正向移动，反而减小 $c(\ce{NH4+})$。
弱碱电离出来的 $c(\ce{NH4+})$ 小于盐类水解产生的 $c(\ce{NH4+})$。

所以相同浓度的 $\ce{(NH4)2SO4}、\ce{NH4Al(SO4)2}、\ce{CH3COONH4}、\ce{NH4Cl}、\ce{NH3.H2O}$，它们的 $c(\ce{NH4+})$ 从大到小排序为：

\[\ce{(NH4)2SO4}>\ce{NH4Al(SO4)2}>\ce{NH4Cl}>\ce{CH3COONH4}>\ce{NH3.H2O} \]

$\ce{pH}$ 相同的 $\ce{(NH4)2SO4}、\ce{NH4Al(SO4)2、\ce{NH4Cl}、\ce{NH4HSO4}}$，它们的 $c(\ce{NH4+})$ 从大到小排序为：

\[\ce{(NH4)2SO4 = NH4Cl > NH4Al(SO4)2 > NH4HSO4} \]

说明：

$\ce{(NH4)2SO4}$ 和 $\ce{NH4Cl}$ 中，只有 $\ce{NH4+}$ 发生水解，即 $\ce{NH4+}$ 是这两杯溶液中能够影响 $c(\ce{H+})$ 的唯一因素。由于其 $\ce{pH}$ 相同，所以它们的 $c(\ce{NH4+})$ 大小相同。
由于

\[\ce{Al^3+ + 3H2O <=> Al(OH)3 + 3H+}\\ \ce{HSO4- = H+ + SO4^2-} \]
即 $\ce{NH4Al(SO4)2}$ 和 $\ce{NH4HSO4}$ 中的 $\ce{Al^3+}$ 和 $\ce{HSO4-}$ 也会影响溶液中的 $c(\ce{H+})$，且 $\ce{HSO4-}$ 电离程度大于 $\ce{Al^3+}$ 水解程度所以影响更大，所以导致 $\ce{NH4+}$ 的影响更小。所以 $\ce{pH}$ 相同（即溶液中的 $c(\ce{H+})$ 相同）的溶液中，$\ce{NH4HSO4}$ 中 $c(\ce{NH4+})$ 最小。

溶液中的微粒关系

解题思路

涉及到与等式有关的问题，考虑写出「电荷守恒」和「元素守恒」，尝试是否能凑出对应的等式。
涉及到溶液中离子浓度大小的比较：

若涉及到有关某离子电离或水解产生的离子之间浓度大小的比较，应考虑溶液中的电离和水解，根据溶液酸碱性，电离和水解的大小关系分析求解；

若仅涉及到溶液中本身的离子，应考虑写出「电荷守恒」根据溶液的酸碱性判断出氢氧根离子浓度的大小，再根据电荷守恒分析出对应的离子浓度关系。
涉及到「滴定」或「溶液中离子浓度动态变化」的问题，可考虑画示意图求解。解题关键：弄清什么时候完全中和。
需要利用电离和水解大小求解的两种情况：①涉及一元弱酸 $\ce{HA}$ 和其钠盐 $\ce{NaA}$ 的混合溶液中离子浓度大小比较的问题：②涉及 $\ce{NaHA}$ 溶液中离子浓度大小的比较问题。

解题技巧

$\ce{NaHCO3 - Na2CO3}$ 混合溶液是指 $\ce{NaHCO3}$ 和 $\ce{Na2CO3}$ 按照 $1:1$ 混合。
比较溶液中的离子浓度大小，应「考虑主要因素，忽略次要因素」。例如，$\ce{NaHCO3}$ 溶液中水解 $>$ 电离。
$\ce{NaHCO3 - Na2CO3}$ 混合溶液中，首先 $c(\ce{Na+})$ 是最大的。然后由于 $\ce{HCO3-}$ 水解程度 $<~\ce{CO3^2-}$ 水解程度，所以 $c(\ce{HCO3-}) > c(\ce{CO3^2-})$。同时 $\ce{HCO3}$ 和 $\ce{CO3^2-}$ 都会电离产生 $\ce{OH-}$，且弱酸的电离程度很小，所以混合溶液中各离子的物质的量浓度关系为：$c(\ce{Na+}) > c(\ce{HCO3-}) > c(\ce{CO3^2-})>c(\ce{OH-})$。
氨水 $-\ce{NH4Cl}$ 混合溶液中的元素守恒为：

\[c(\ce{NH4+}) + c(\ce{NH3*H2O}) = 2c(\ce{Cl-}) \]
等浓度、等体积的弱酸（弱碱）和对应的弱酸盐（弱碱盐） $1:1$ 混合，得到的混合溶液中质子守恒为：

\[c(弱酸/弱碱) + 2c(\ce{H+}) = c(弱酸根/弱碱根) + 2c(\ce{OH-}) \]
$\ce{CH3COOH - CH3COONa}$ 混合溶液 $(\ce{pH = 4.76})$ 中，若不考虑电离和水解，则溶液中 $c(\ce{CH3COOH}) = c(\ce{Na+}) = c(\ce{CH3COO-})$由于溶液为酸性，所以 $\ce{CH3COOH}$ 的电离 $>$ $\ce{CH3COO-}$ 的水解，所以 $c(\ce{CH3COOH}) < c(\ce{CH3COO-})$。又因为 $c(\ce{Na+})$ 不变，所以 $c(\ce{CH3COO-}) > c(\ce{Na+})> c(\ce{CH3COOH})$。同时，由于水的电离程度很小，所以氢离子和氢氧根离子的浓度小于主要物质，且由于溶液是酸性，所以 $c(\ce{H+}) > c(\ce{OH-})$。
在 $\pu{0.1 mol*L-1}\ \ce{NaHCO3}$ 溶液中 $\ce{HCO3-}$ 及其电离或水解出的所有离子（水溶液中存在的所有形态）物质的量浓度之和为 $\pu{0.1 mol*L-1}$，所以 $c(\ce{H2CO3}) + c(\ce{HCO3-}) +c(\ce{CO3^2-})= \pu{0.1 mol*L-1}$。
氨水和 $\ce{NH4Cl}$ 溶液混合，形成 $\ce{pH = 9}$ 的溶液中，电荷守恒为：

\[c(\ce{H+}) + c(\ce{NH4+}) = c(\ce{Cl-}) + c(\ce{OH-}) \]
由于 $\ce{pH = 9}$，所以 $c(\ce{H+}) < c(\ce{OH-})$，所以 $c(\ce{NH4+}) > c(\ce{Cl-})$。
对于题目中涉及到「中性溶液」的问题，一般优先考虑写出电荷守恒。中性溶液中，$c(\ce{H+}) = c(\ce{OH-})$。
相同浓度的两种钠盐，$\ce{pH}$ 大的对应的酸酸性越弱，$K_a$ 越小。
对于弱酸，$K_w = K_h \cdot K_{a}$。
设 $\ce{H2C2O4}$ 溶液中 $c(\ce{总}) = c(\ce{H2C2O4}) +c(\ce{HC2O4-}) + c(\ce{C2O4^2-})$，室温下用 $\ce{NaOH}$ 溶液滴定 $\pu{25.00mL~ 0.1000 mol*L-1}~\ce{H2C2O4}$ 溶液至终点。在滴定过程中，由于滴定导致体积的增加，溶液的总物质的量浓度不断减小，所以物质的量浓度 $< \pu{0.1 mol*L-1}$。
注意原来浓度为 $x$ 的溶液，加入新的其它溶液，或滴定其它溶液，得到混合溶液的浓度不再是 $x$，而应该 $< x$。
$\pu{0.2 mol*L-1}$ 氨水中，由于 $\ce{NH3*H2O}$ 和 $\ce{H2O}$ 都会电离产生 $\ce{OH-}$，所以 $c(\ce{OH-}) > c(\ce{NH4+})$。或者从电荷守恒来说，因为 $c(\ce{H+}) +c(\ce{NH4+}) = c(\ce{OH-})$，且 $c(\ce{H+})\ne 0$，所以 $c(\ce{OH-}) >c(\ce{NH4+})$。

注意：「完全中和」不等于「中性溶液」，对于涉及中性溶液的问题，应先找到当溶液「完全中和」时的溶液酸碱性，再进行分析。

例如：常温下，用 $\pu{0.1 mol*L-1}$ 氨水滴定 $\pu{10 mL}$ 浓度均为 $\pu{0.1 mol*L-1}$ 的 $\ce{HCl}$ 和 $\ce{CH3COOH}$ 的混合溶液。由于当溶液完全中和时，氨水滴入量为 $\pu{20mL}$，是 $\ce{CH3COONH4}$ 和 $\ce{NH4Cl}$ 的混合溶液，其中，$\ce{CH3COONH4}$ 高中阶段默认为中性溶液，$\ce{NH4Cl}$ 是强酸弱碱盐，是酸性溶液。所以溶液完全中和时，溶液呈酸性。当溶液呈现中性时，氨水滴入量大于 $\pu{20 mL}$，$c(\ce{NH4+}) >c(\ce{Cl-})$。

经典酸碱中和滴定 $\ce{pH - V}$ 图像分析

解题步骤

判断是「酸滴碱」还是「碱滴酸」；
判断两者何时「完全中和」。（注意这里是「完全中和」而不是「呈中性」）
求出恰好完全中和时溶液中的溶质以及溶液中的 $\ce{pH}$：正盐溶液，谁强显谁性；
根据题意求解。

解题要点及注意事项

注意根据题目要求辨别其考察的题型，从而根据每个题型的求解方法求解。

注意：实际上下面的解题要点大都在上文中的不同题型的解题方法中提过，但为了更快更熟练的求解题目，这里将常用的考点&要点总结整合一下。

「强酸滴定弱碱」溶液显酸性，用甲基橙作为指示剂；「强碱滴定弱酸」溶液显碱性，用酚酞作为指示剂。
遇到中性溶液中的离子浓度问题，要想到「电荷守恒」。
「完全中和」$\ne$ 「中性」，求解溶液呈中性是体积的相关问题时，应该先抓「特殊点」随后再进行微调。
溶液中的主要离子浓度都大于次要离子浓度（一般是 $\ce{H+}$ 和 $\ce{OH-}$）。
求解溶液 $\ce{pH}$ 的问题，且已知起始浓度和电离度，一般采用三段式。
求解不同酸的电离常数，一般比较未滴定时的 $\ce{pH}$，$\ce{pH}$ 越小，$c(\ce{H+})$ 越大，$K_a$ 越大。或者也可以比较对应正盐，即对应盐类的 $\ce{pH}$ 越高，其水解程度越大，根据越弱越水解，它对应的酸酸性就越弱，从而电离常数 $K_a$ 越小。
对于「恰好中和一半」的理解：溶液中有等量的弱酸及其盐。此时一般需观察溶液的 $\ce{pH}$，从而根据 $\ce{pH}$ 判断出溶液中电离和水解的大小关系从而求解。此时溶液中的质子守恒（以 $\ce{CH3COOH}$ 被 $\ce{NaOH}$ 滴定为例）：

\[c(\ce{CH3COOH}) + 2c(\ce{H+}) = c(\ce{CH3COO-}) + 2c(\ce{OH-}) \]
中和浓度相同的三种酸性不同的弱酸，达到中性时需要的碱的量不同，所以此时虽然由于电荷守恒，弱酸跟离子物质的量浓度等于对应碱中非氢氧根离子的浓度，但由于碱的量不同，所以弱酸根离子的物质的量浓度也不同。
当中和百分数达到 $100\%$，或「完全中和」时，说明此时的溶液是一杯正盐水溶液。
完全中和浓度相同的酸性不同的 $n$ 元酸，需要的碱的量相同。
比较不同溶液中离子的浓度大小，尤其是不同溶液中存在浓度相同的某种离子时，应该写出每种溶液的电荷守恒，再根据浓度相同的离子比较大小。
一元强碱滴定二元弱酸时，可视为「两次中和」，即：

第一次：当一元强碱与二元弱酸的物质的量之比为 $1:1$ 时，有（以氢氧化钠作为一元强碱为例）：

\[\ce{H2A + NaOH = NaHA + H2O} \]
第二次：当一元强碱与二元弱酸的物质的量之比为 $2:1$ 时，有：

\[\ce{H2A + 2NaOH = Na2A + 2H2O} \]
滴定过程中体积会膨胀，所以若滴定初始时被滴定溶液的物质的量浓度为 $x\ \pu{mol*L-1}$，则滴定后的（或滴定过程中）溶液应该小于 $x\ \pu{mol*L-1}$。
题目中若出现比较特殊的 $\ce{pH}$，例如已知某二元弱酸 $\ce{H2A}$ 的 $-\lg K_{a_1} = 1.23$，然后图像中有某点 $\ce{pH}$ 为 $1.23$，可考虑将二元弱酸的第一步电离拆解观察，例如：

\[K_{a_1} = \dfrac{c(\ce{H+})\cdot c(\ce{HA-})}{c(\ce{H2A})} \]
观察可知，当 $\ce{pH} = 1.23$ 时，恰好有 $c(\ce{HA-}) = c(\ce{H2A})$，可利用其求解问题。
题目中所说的「反应终点」，一般指「完全中和点」。
离子的导电能力与其单个离子的电子数有关，一般电子数越大，导电能力越强。
用同浓度盐酸滴定同浓度碳酸氢钠溶液，完全中和时溶液中虽然会产生 $\ce{CO2}$ 和 $\ce{H2O}$，但并不是所有的碳都会转化成 $\ce{CO2}$，溶液中还有一部分 $\ce{H2CO3}$。
同浓度的 $\ce{NaOH}$ 溶液和 $\ce{NaHCO3}$ 溶液混合，得到的 $\ce{Na+}$ 浓度始终保持不变。
比较有关 $K_a,K_h,K_w$ 大小的题目要注意电离与水解的关系，以及他们仨之间存在怎样的等式。
有关水的电离平衡问题，牢记：抑制水电离 $\to$ 加酸或加碱；促进水电离 $\to$ 可水解的盐。所以一般酸碱滴定中水的电离程度是先增大后减小。

分布分数图像分析

物质的量分数与 $\ce{pH}$ 图像

关键点：对应两个物质的曲线交点。

例如：改变 $\pu{0.1 mol*L-1}$ 二元弱酸 $\ce{H2A}$ 溶液的 $\ce{pH}$ 的分布分数图像如下。

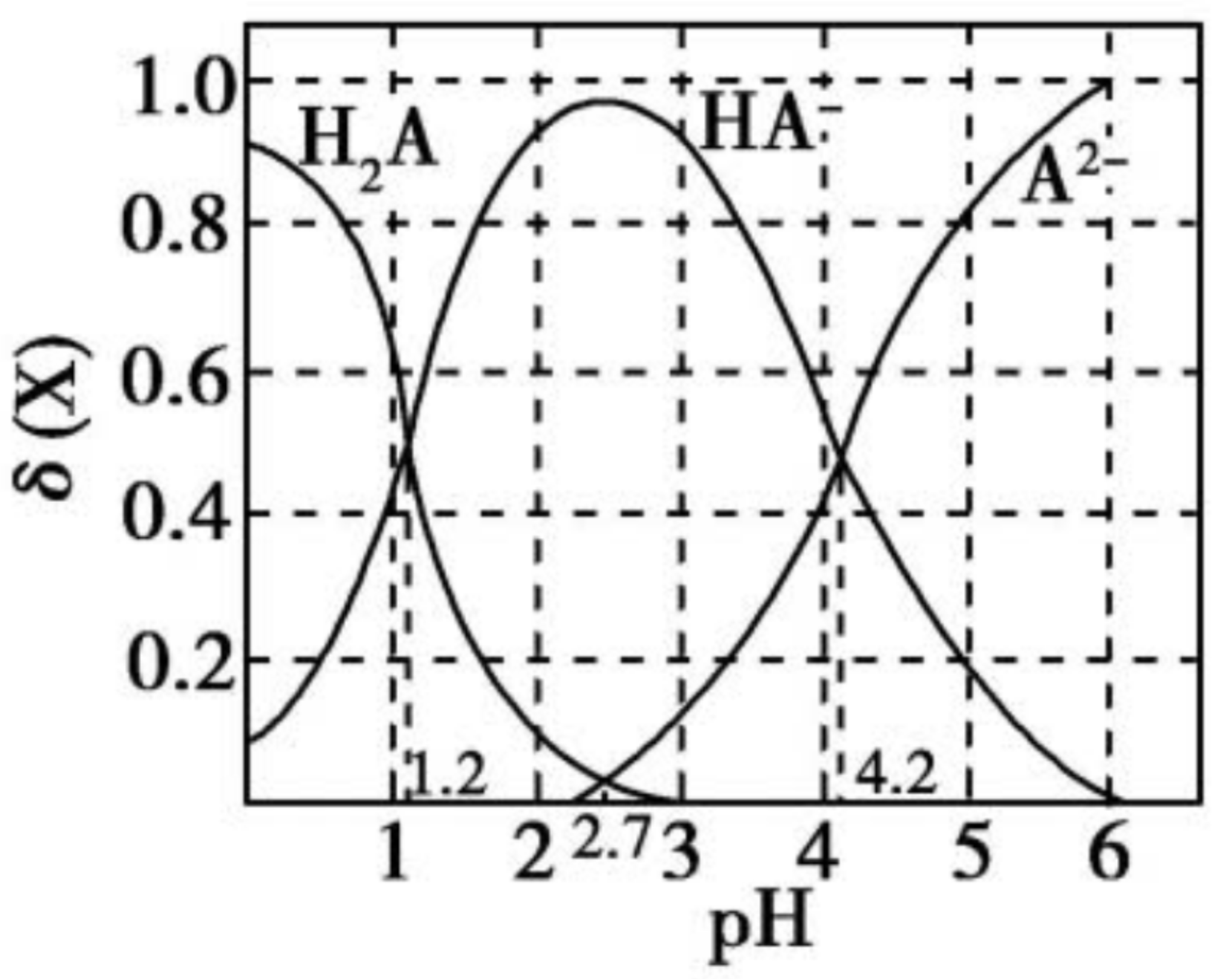
则对于图中第一个交点，说明 $c(\ce{H2A}) = c(\ce{HA-})$，由于

\[K_{a_1} = \dfrac{c(\ce{H+})\cdot c(\ce{HA-})}{c(\ce{H2A})} \]

所以 $K_{a_1} = c(\ce{H+})$。由于 $\ce{pH = 1.2}$，所以 $ c(\ce{H+}) = \pu{10^{-1.2} mol*L-1}$，即 $K_{a_1} = 10^{-1.2}$。

同理，根据图中第三个交点得到 $K_{a_2} = 10^{-4.2}$。同时若改变 $\ce{pH}$ 前后溶液体积不变，则第三个交点时，$c(\ce{HA-}) = c(\ce{A^2-}) = \pu{0.05 mol*L^-1} > c(\ce{H+}) = \pu{10^{-4.2} mol*L-1}$。

那么 $\ce{NaHA}$ 中 $\ce{HA-}$ 的水解平衡常数为：

\[K_h = \dfrac{K_w}{K_{a_1}} = \dfrac{10^{-14}}{10^{-1.2}} = 10^{-12.8} \]

所以 $\ce{NaHA}$ 的电离平衡常数 $K_{a_2} \gg $ 水解平衡常数 $K_h$，所以 $\ce{NaHA}$ 在常温下 $\ce{pH < 7}$。

对于图中第二个交点，即 $c(\ce{H2A}) = c(\ce{A^2-})$，有：

\[K_{a_1} \times K_{a_2} = \dfrac{c(\ce{H+})\cdot c(\ce{HA-})}{c(\ce{H2A})}\times \dfrac{c(\ce{H+})\cdot c(\ce{A^2-})}{c(\ce{HA-})} = \dfrac{c^2(\ce{H+})\cdot c(\ce{A^2-})}{c(\ce{H2A})} =c^2(\ce{H+}) \]

所以

\[\begin{aligned} &c(\ce{H+}) = (K_{a_1}\cdot K_{a_2})^{\frac{1}{2}}\\\Longrightarrow &\ce{pH} = -\lg c(\ce{H+}) = -\lg (K_{a_1}\cdot K_{a_2})^{\frac{1}{2}} = -\dfrac{1}{2}(K_{a_1}\cdot K_{a_2}) = -\dfrac{1}{2}K_{a_1} - \dfrac{1}{2}\lg K_{a_2} \end{aligned} \]

浓度之比的 $\lg$ 值与 $\ce{pH}$ 图像

关键点：$\lg$ 值为 $0$，即两种物质的浓度相等的点。

例如：常温下将 $\ce{NaOH}$ 溶液滴加到己二酸 $\ce{H2X}$ 溶液中，混合溶液的 $\ce{pH}$ 与离子浓度变化的关系如图所示。

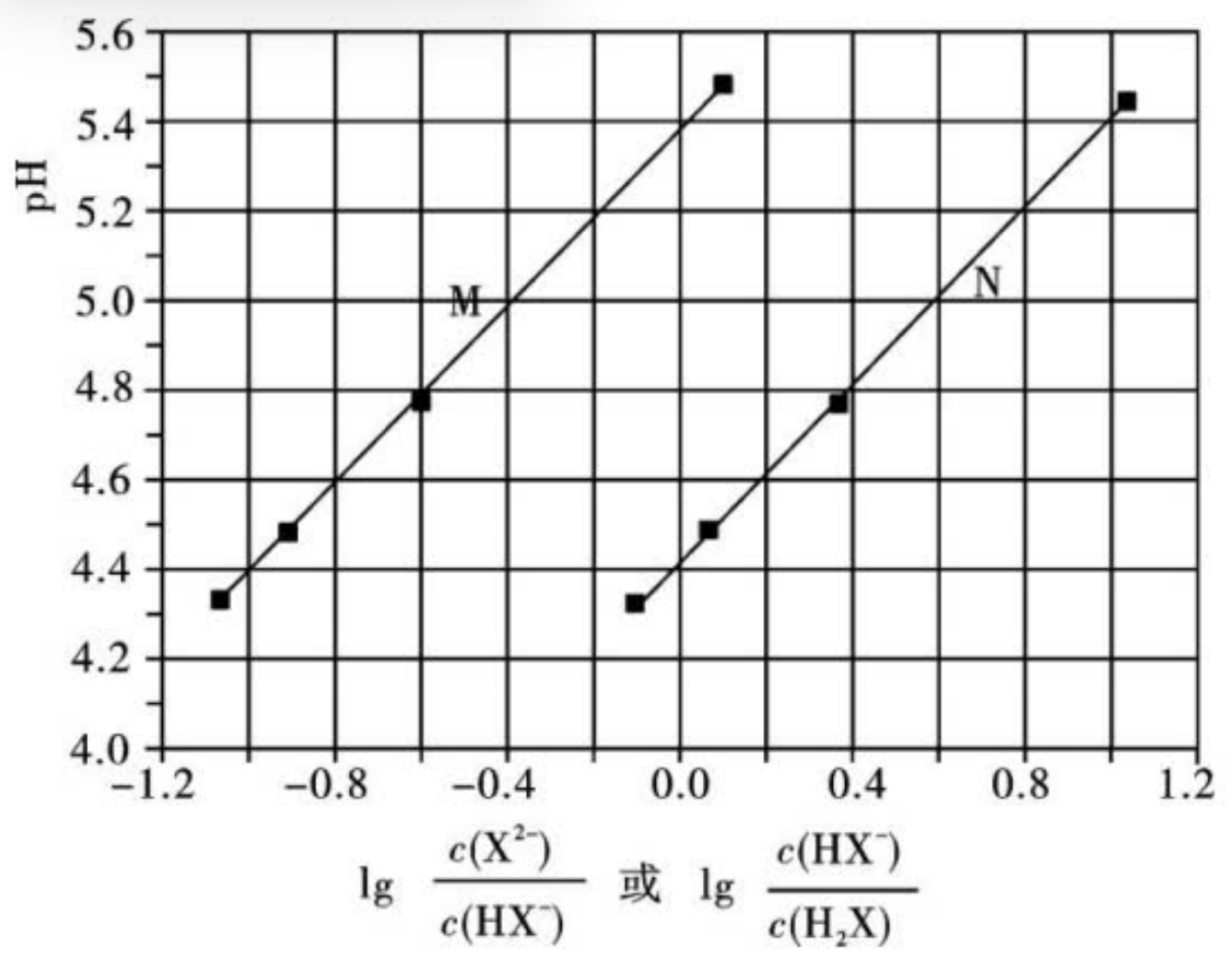
当 $\lg \dfrac{c(\ce{X^2-})}{c(\ce{HX-})} = 0$ 时，$c(\ce{X^2-}) = c(\ce{HX- })$，由于

\[K_{a_2} = \dfrac{c(\ce{H+})\cdot c(\ce{X^2-})}{c(\ce{HX-})} \]
当 $\lg \dfrac{c(\ce{HX-})}{c(\ce{H2X})} = 0$ 时，$c(\ce{HX-}) = c(\ce{H2X})$，由于

\[K_{a_1} = \dfrac{c(\ce{H+})\cdot c(\ce{HX-})}{c(\ce{H2X})} \]

由于 $K_{a_1} > K_{a_2}$，所以 $K_{a_1} = 10^{-4.4}$，$K_{a_2} = 10^{-5.4}$。从而可以判断出 $M$ 曲线表示的是 $\lg \dfrac{c(\ce{X^2-})}{c(\ce{HX-})}$，$N$ 曲线表示的是 $\lg \dfrac{c(\ce{HX-})}{c(\ce{H2X})}$。

判断混合溶液中离子浓度的关系也可以利用 $K_a$。

例如当混合溶液呈中性时，$c(\ce{OH-}) = c(\ce{H+}) = \pu{10^-7 mol*L-1}$，根据 $K_{a_2}$ 的表达式可得

\[\dfrac{c(\ce{X^2-})}{c(\ce{HX-})} = \dfrac{K_{a_2}}{c(\ce{H+})} = 10^{1.6} >1 \]

所以 $c(\ce{H+}) > K_{a_2}$。

或者也可以由图像得到：

当 $\ce{pH = 7}$ 时，$\lg \dfrac{c(\ce{X^2-})}{c(\ce{HX-})} >0$，即 $\dfrac{c(\ce{X^2-})}{c(\ce{HX-})} >1$，说明 $c(\ce{X^2-}) > c(\ce{HX-})$。

有关数量级的定义：

对于 $a\times 10^b$，其中 $1 \le a < 10$，即 $10^0 \le a < 10^1$，数量级为 $10^b$。所以 $10^{5.4} = 10^{0.6}\times 10^{-6}$，即数量级为 $10^{-6}$。

沉淀溶解平衡

基本概念

概念

在一定温度下，当沉淀和溶解的速率相等时，形成饱和溶液，达到平衡状态，把这种平衡称为沉淀溶解平衡。

建立

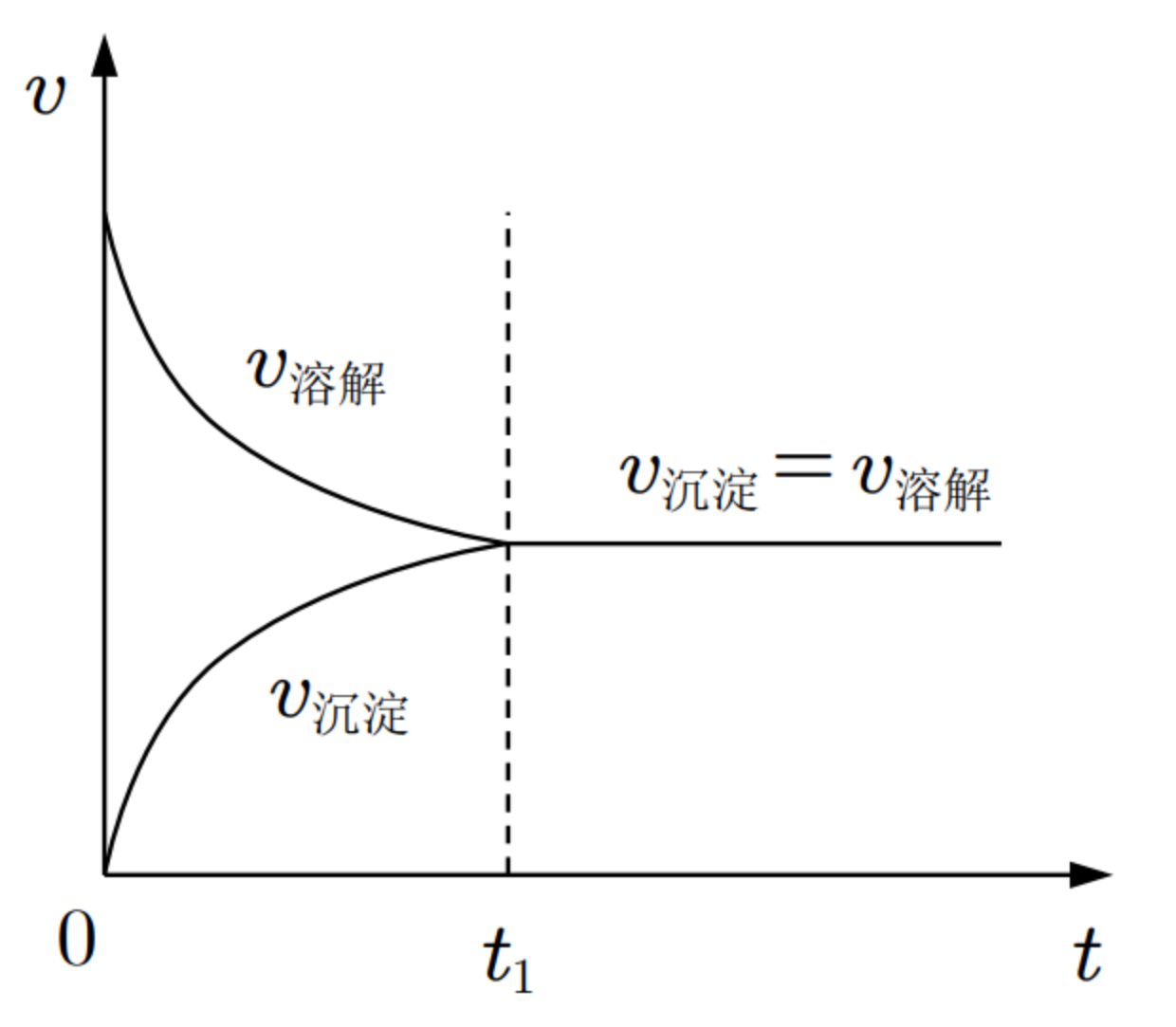
方程式

\[\ce{M_mA_n(s) <=> m M^n+(aq) + n A^m-(aq)} \]

例如，$\ce{AgCl}$ 沉淀溶解平衡方程式为：

\[\ce{AgCl(s) <=> Ag+ (aq) + Cl- (aq)} \]

注意：写沉淀溶解平衡方程式时，为了与电解质电离区分开来，必须要写状态。

影响因素

内因

难溶电解质本身的性质是主要决定因素。

外因

温度、浓度、同离子效应等，其影响符合「勒夏特列原理」。

温度：绝大多数难容盐的溶解是吸热过程，升高温度，平衡向溶解的方向移动，少数平衡向生成沉淀的方向移动，如 $\ce{Ca(OH)2}$ 的溶解平衡。
同离子效应：假如与电解质电离的离子相同的可溶性盐，平衡向生成沉淀的方向移动，溶解度减小。
外加其他物质：向平衡体系中加入可与体系中某些离子反应生成更难溶、或更难电离、或气体的离子，或与电解质电离的离子反应时，平衡向溶解的方向移动。例如，在 $\ce{CuS}$ 溶液中加入 $\ce{HNO3}$，可以氧化 $\ce{S^2-}$，降低溶液中的 $\ce{S^2-}$ 含量，从而使平衡正向移动。

溶度积 $K_{sp}$ 的概念与表达式

定义

在一定温度下，沉淀溶解平衡的平衡常数称为溶度积常数，简称溶度积，用 $K_{sp}$ 表示。

表达式

对于沉淀溶解平衡：

\[\ce{M_mA_n(s) <=> m M^n+ (aq) + n A^m- (aq)} \]

其中：

\[K_{sp} = c^m(\ce{M^n+})\cdot c^n(\ce{A^m-}) \]

注意：$K_{sp}$ 的表达式不用除以 $c(\ce{M_mA_n})$。

意义

溶度积 $K_{sp}$ 反应了物质在水中的溶解能力。

对于阴、阳离子个数比相同的电解质（相同类型的电解质溶液），$K_{sp}$ 的数值越大，电解质在水中的溶解能力越强；数值越小，溶解度越小（越难溶）。

影响因素

溶度积 $K_{sp}$ 只与难溶电解质的性质和温度有关，一般温度越高，$K_{sp}$ 增大。

应用

以 $\ce{AgCl(s) <=> Ag+(aq) + Cl- (aq)}\quad \Delta H >0$ 为例（$\ce{AgCl}$ 固体足量）：

外界条件	移动方向	平衡后 $c(\ce{Ag+})$	平衡后 $c(\ce{Cl-})$	$K_{sp}$
升高温度	正向移动	增大	增大	增大
加水稀释	正向移动	不变	不变	不变
加入少量 $\ce{AgNO3}$	逆向移动	增大	减小	不变
通入 $\ce{HCl}$	逆向移动	减小	增大	不变
通入 $\ce{H2S}$	正向移动	降低	增大	不变

说明：

加水稀释后，$c(\ce{Ag+})$ 和 $c(\ce{Cl-})$ 会减小，同时又因为 $\ce{AgCl}$ 固体足量，所以 $\ce{AgCl}$ 会无限补充，不断溶解，平衡正向移动，从而使得 $c(\ce{Ag+})$ 和 $c(\ce{Cl-})$ 不断增大，直至与原来相同，所以最终 $c(\ce{Ag+})$ 和 $c(\ce{Cl-})$ 不变。注意：这里由于 $\ce{AgCl}$ 固体足量可以无限补充，所以不符合「勒夏特列原理」，这一点与盐类水解和水的电离不同。
通入 $\ce{H2S}$ 固体后，由于 $\ce{H2S}$ 固体难溶，其会与 $\ce{Ag+}$ 反应生成 $\ce{Ag2S}$ 沉淀，使得溶液中的 $c(\ce{Ag+})$ 减小，从而使得平衡正向移动，$c(\ce{Cl-})$ 增大。

溶度积 $K_{sp}$ 与溶解度

对于阴、阳离子个数比相同的难溶电解质，$K_{sp}$ 越大，说明难溶电解质在水中的溶解能力越大。例如：$K_{sp}(\ce{AgCl}) > K_{sp}(\ce{AgBr}) > K_{sp}(\ce{AgI})$，则溶解度：$S(\ce{AgCl}) > S(\ce{AgBr}) > S(\ce{AgI})$。
对于阴、阳离子个数比不同的电解质，$K_{sp}$ 小的电解质的溶解度不一定比 $K_{sp}$ 大的溶解度小。例如：$K_{sp}(\ce{Ag2CrO4}) < K_{sp}(\ce{AgCl})$，但 $\ce{Ag2CrO4}$ 的溶解度大于 $\ce{AgCl}$ 的溶解度。因此，不能通过比较 $K_{sp}$ 数值的大小来确定溶解度的大小。

例：已知 $K_{sp}(\ce{AgCl}) = 1.56 \times 10^{-10},K_{sp}(\ce{AgBr}) = 7.7 \times 10^{-13},K_{sp}(\ce{Ag2Cr2O4}) = 9.0 \times 10^{-12}$，某溶液中含有 $\ce{Cl- 、Br-}$ 和 $\ce{CrO4^2-}$，浓度均为 $\pu{0.01 mol*L-1}$，向该溶液中逐滴加入 $\pu{0.01 mol*L-1}$ 的 $\ce{AgNO3}$ 溶液时，三种阴离子产生沉淀的先后顺序是什么。

首先，$\ce{AgCl}$ 和 $\ce{AgBr}$ 是阴、阳离子个数比相同的难溶电解质，由于 $K_{sp}(\ce{AgCl}) > K_{sp}(\ce{AgBr})$，所以 $\ce{AgCl}$ 在水中的溶解度更大。

设 $\ce{Ag2CrO4}$ 中 $\ce{Ag+}$ 被溶解掉了 $2x$，则根据 $\ce{Ag2CrO4(s) <=> 2Ag+(aq) + CrO4^2-(aq)}$，可知 $\ce{CrO4^2-}$ 被溶解了 $x$，那么根据溶度积可得 $(2x)^2 \cdot x = 4x^3 = 9\times 10^{-12}$，所以 $x \approx \pu{10^-4 mol*L-1}$，同理，设 $\ce{AgCl}$ 中 $\ce{Ag+}$ 被溶解掉了 $y$，则有 $y^2 = 1.56\times 10^{-10}$，所以 $y \approx \pu{10^{-5} mol*L-1}$。所以 $\ce{Ag2CrO4}$ 的溶解度更大。

综上，三种溶质的溶解度为 $S(\ce{Ag2CrO4}) > S(\ce{AgCl}) > S(\ce{AgBr})$，所以三种阴离子产生沉淀的先后顺序是 $\ce{Br- 、Cl- 、CrO4^2-}$。

溶度积 $K_{sp}$ 与离子积 $Q$

根据某温度下难溶电解质的溶度积与该溶液中的离子积 $Q$ 的相对大小，可以判断该温度下的溶液中难溶电解质的沉淀或溶解情况。

以 $\ce{A_m + B_n(s) <=> m A^n+ (aq) + n B^m- (aq)}$ 为例：

	溶度积	离子积
概念	沉淀溶解的平衡常数	溶液中有关离子浓度幂的乘积
符号	$K_{sp}$	$Q$
表达式	$K_{sp}(\ce{A_m B_n}) = c^m(\ce{A^n+})\cdot c^n(\ce{B^m-})$ 式中的浓度为平衡浓度	$Q_c(\ce{A_mB_n}) = c^m(\ce{A^n+})\cdot c^n(\ce{B^m-})$ 式中的浓度时任意浓度

应用——判断在一定条件沉淀能否生成或溶解：

$Q_c < K_{sp}$：溶液不饱和，无沉淀析出。
$Q_c = K_{sp}$：溶液饱和，沉淀与溶解处于平衡状态。
$Q_c > K_{sp}$：溶液过饱和，有沉淀析出。

应用

沉淀的生成

应用

在无机物的制备和提纯、废水处理等领域，常利用生成沉淀来达到分离或除去某些离子的目的。

方法

调节 $\ce{pH}$ 法：
- 除去 $\ce{NH4Cl}$ 中的 $\ce{FeCl3}$：溶于水，加氨水调节 $\ce{pH}$，方程式
  
  \[\ce{Fe^3+ + 3NH3*H2O = Fe(OH)3 v + 3NH4+} \]
- 除去 $\ce{CuCl2}$ 中的 $\ce{FeCl3}$：加入 $\ce{Cu(OH)2}$ 或 $\ce{CuO}$，方程式
  
  \[\ce{Fe^3+ + 3H2O <=> Fe(OH)3 + 3H+}\\ \ce{Cu(OH)2 + 2H+ = Cu^2+ + 2H2O}\\ \ce{CuO + 2H+ = Cu^2+ + 2H2O} \]
沉淀剂法：
- 除去废水中的 $\ce{Hg^2+}$：加入 $\ce{Na2S}$，方程式
  
  \[\ce{S^2- + Hg^2+ = HgS v} \]
- 除去废水中的 $\ce{Cu^2+}$：通入 $\ce{H2S}$，方程式
  
  \[\ce{H2S + Cu^2+ = CuS v + 2H+} \]

注意：$\ce{Ag+,Cu^2+,Pb^2+,Hg^2+}$ 用 $\ce{S^2-}$ 会形成极难溶沉淀。

沉淀的溶解

原理

在实际应用中，常常会遇到需要使难溶物质溶解的问题. 根据平衡移动原理，对于在水中难溶的电解质，如果能设法不断地移去平衡体系中的相应离子，使平衡向溶解方向移动，就可以使沉淀溶解，如 $\ce{CaCO3}$ 沉淀可溶于盐酸中。

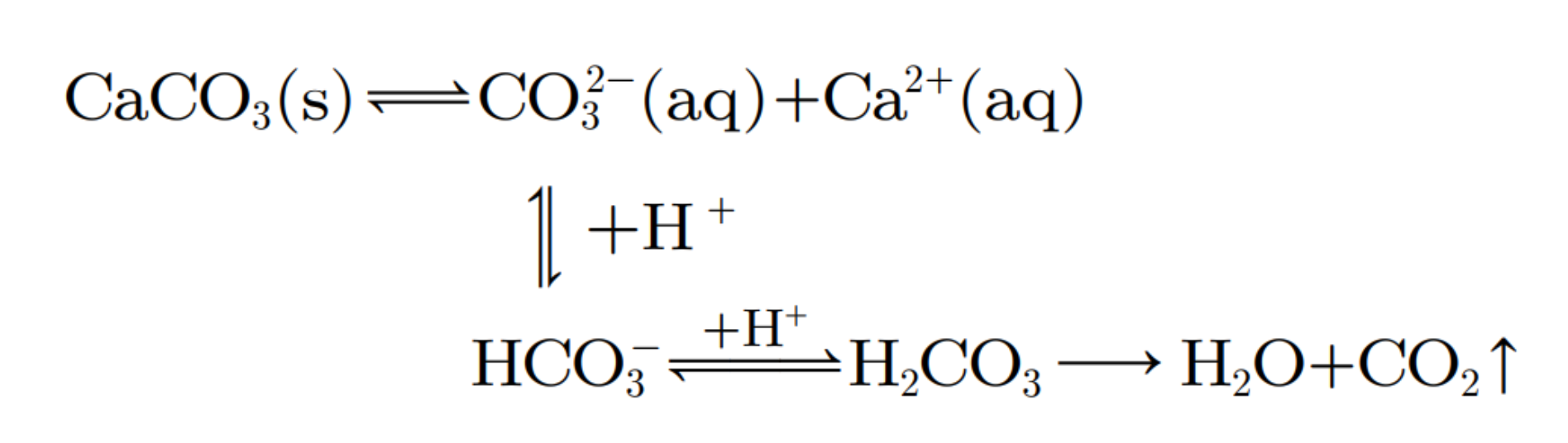
应用

实验操作	实验现象	原因解释

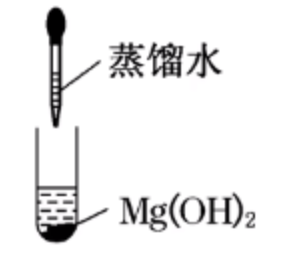白色沉淀	难溶于水

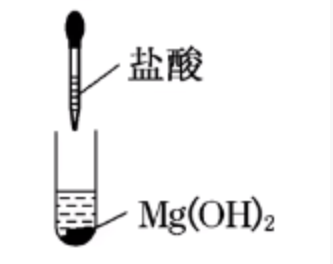白色沉淀溶解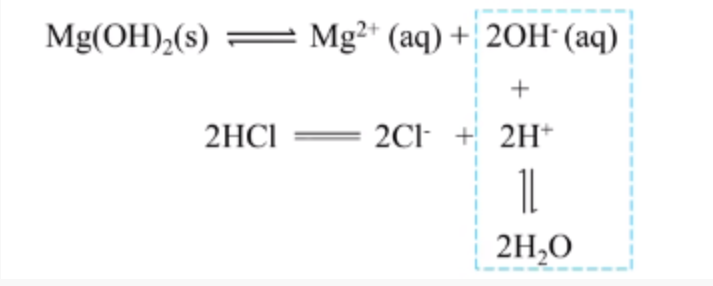


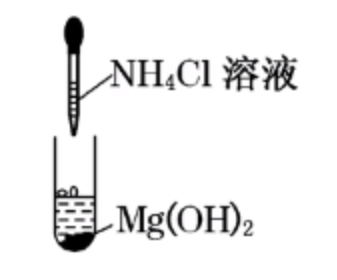白色沉淀溶解	溶液中原有平衡：$\ce{Mg(OH)2(s) <=> Mg^2+(aq) + 2OH-(aq)}$ 加入 $\ce{NH4Cl}$ 后，有 $\ce{NH4+ + OH- = NH3*H2O}$，从而使得溶液中 $c(\ce{OH-})$ 降低，平衡正向移动，$\ce{Mg(OH)2}$ 溶解。

结论：$\ce{Mg(OH)2}$ 沉淀不仅能被盐酸溶解，还能被 $\ce{NH4Cl}$ 溶解。

总结——沉淀溶解的方法

酸溶法：如 $\ce{CaCO3}$ 溶于盐酸，$\ce{Al(OH)3}、\ce{Cu(OH)2}$ 溶于强酸等。
盐溶法：如 $\ce{Mg(OH)2}$ 可溶于 $\ce{NH4Cl}$ 溶液中，方程式：

\[\ce{Mg(OH)2 + 2 NH4+ = Mg^2+ + 2NH3*H2O} \]
氧化还原法：如 $\ce{Cu2、HgS}$ 等可溶于 $\ce{HNO3}$ 中，方程式：

\[\ce{3CuS + 8HNO3 = 3Cu(NO3)2 + 3S + 2NO ^ + 4H2O} \]
配合物法：如 $\ce{AgCl}$ 可溶于 $\ce{NH3*H2O}$，方程式：

\[\ce{AgCl + 2NH3*H2O = [Ag(NH3)2]+ + Cl- + 2H2O} \]

沉淀的转化

实验一—— $\ce{AgCl、AgI、Ag2S}$ 的转化

实验操作：如图所示。

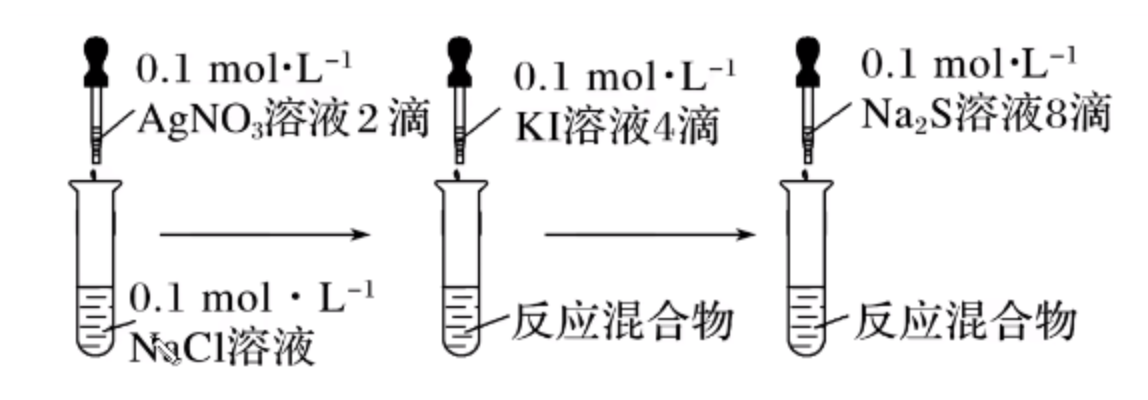
实验现象：

第一步操作后：有白色沉淀生成。
第二步操作后：白色沉淀转化为黄色沉淀。
第三步操作后：黄色沉淀转化为黑色沉淀。

实验原理：

\[\ce{Ag+(aq) + Cl-(aq) <=> AgCl(s) }\\ \ce{AgCl(s) + KI(aq) <=> AgI(s) + KCl(aq)}\\ \ce{2AgI(s) + Na2S(aq) <=> Ag2S(s) + 2NaI(aq)} \]

实验结论：

溶解度：$\ce{Ag2S < AgI < AgCl}$。

注意：结论是溶解度之间的大小比较，而非 $K_{sp}$。

实验二—— $\ce{Mg(OH)2}$ 与 $\ce{Fe(OH)3}$ 的转化

实验操作：如图所示。

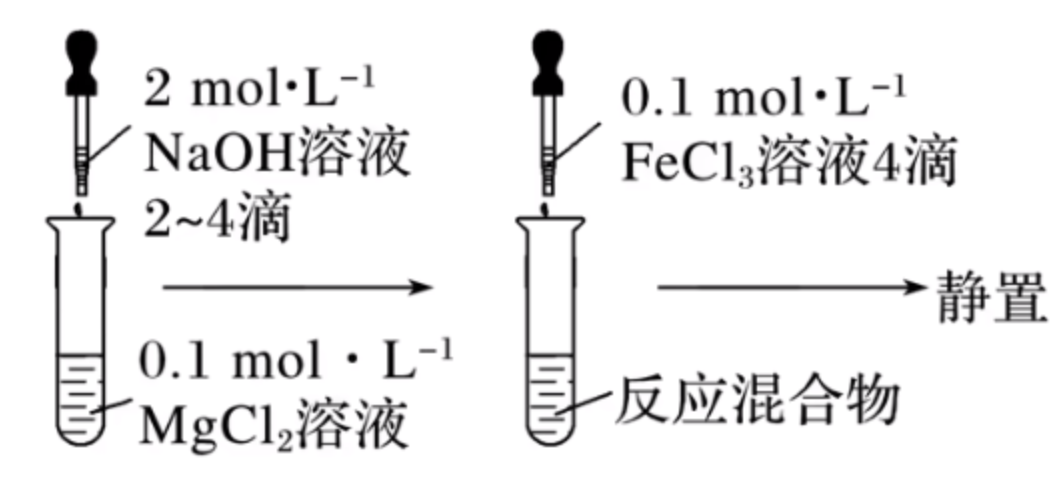
实验现象：

第一步操作后：有白色沉淀产生。
第二步操作后：白色沉淀转化为红褐色沉淀。

实验原理：

\[\ce{Mg^2+(aq) + 2OH-(aq) <=> Mg(OH)2(s) }\\ \ce{3Mg(OH)2(s) + 2FeCl3(aq) <=> 2Fe(OH)3(s) + 3MgCl2(aq)} \]

实验结论：

$\ce{Mg(OH)2}$ 沉淀转化为 $\ce{Fe(OH)3}$ 沉淀，说明溶解度 $\ce{Fe(OH)3 < Mg(OH)3}$。

规律

溶解度小的沉淀转化为溶解度更小的沉淀容易实现，溶解度相差越大，转化越容易。

实际生活中的应用

锅炉除水垢（含有 $\ce{CaSO4}$）

操作：先加 $\ce{Na2CO3}$ 溶液，再加稀盐酸。

原理：

根据 $\ce{CaSO4}$ 是微溶物，$\ce{CaCO3}$ 是难溶物，前者溶解度大于后者，可以有：

\[\ce{CaSO4(s) + Na2CO3(aq) <=> CaCO3(s) + Na2SO4(aq)}\\ \ce{CaCO3 + 2HCl = CaCl2 + H2O + CO2} \]

补充：高中四大微溶物：$\ce{Ag2SO4}、\ce{CaSO4}、\ce{Ca(OH)2}、\ce{MgCO3}$。

自然界中的矿物的转化

\[原生铜的硫化物 \ce{->[氧化、淋滤]\ce{CuSO4}~ 溶液 \ce{->[渗透、遇闪锌矿(ZnS)和方铅矿(PbS)]} 铜蓝(CuS)} \]

原理：$\ce{ZnS}$ 和 $\ce{PbS}$ 可以转化成与其相比溶解度更小的 $\ce{CuS}$。

氟化物预防龋齿

牙齿表面的釉质层，主要成分是难溶的羟基磷灰石 $\ce{[Ca5(PO4)3(OH)]}$。口腔中的有机酸使釉质层溶解：

\[\ce{Ca5(PO4)3(OH) + 4H+ = 5Ca^2+ + 3HPO4^2- + H2O} \]

氟离子能与羟基磷灰石反应，生成溶解度更小的氟磷灰石，更能抵抗酸的腐蚀：

\[\ce{Ca5(PO4)3(OH)(s) + F-(aq) <=> Ca5(PO4)3F(s) + OH-(aq)} \]

其中含氟牙膏就用的是这个原理。

平衡图像分析

例题

例（2021 全国乙卷）：$\ce{HA}$ 是一元弱酸，难溶盐 $\ce{MA}$ 的饱和溶液中 $c(\ce{M+})$ 随着 $c(\ce{H+})$ 而变化，$\ce{M+}$ 不发生水解。实验发现，$\pu{298 K}$ 时 $c^2(\ce{M+})\sim c(\ce{H+})$ 为线性关系，如图中实线所示。下列叙述错误的是（）

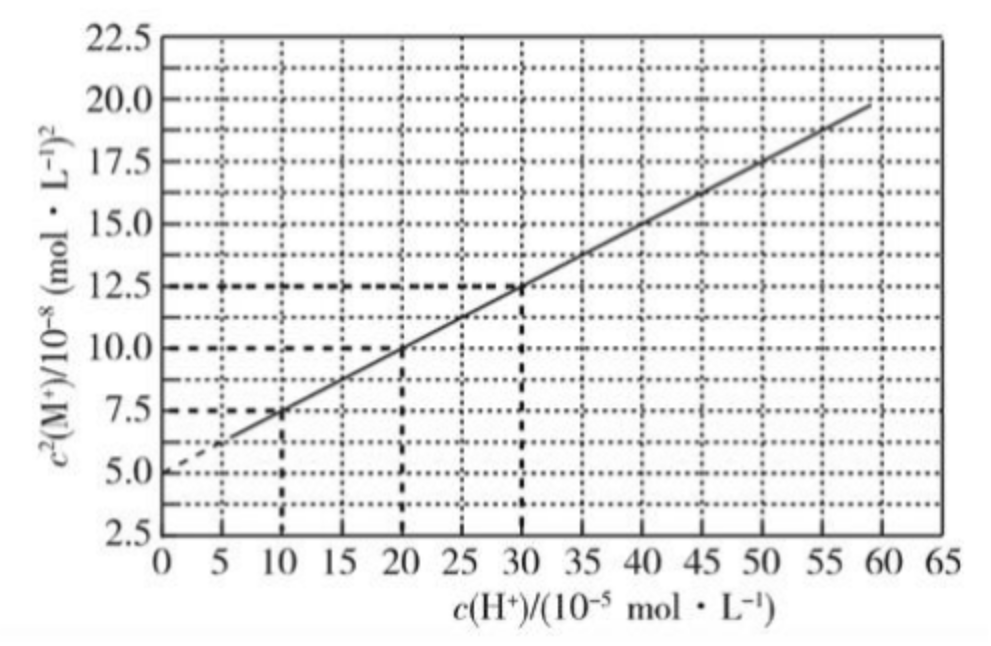
A. 溶液 $\ce{pH = 4}$ 时，$c(\ce{M+}) < \pu{3.0E-4 mol*L-1}$

B. $\ce{MA}$ 的溶度积 $K_{sp}(\ce{MA}) = \pu{5.0E-8}$

C. 溶液 $\ce{pH = 7}$ 时，$c(\ce{M+}) + c(\ce{H+}) = c(\ce{A-}) + c(\ce{OH-})$

D. $\ce{HA}$ 的电离常数 $K_a(\ce{HA}) \approx \pu{2.0E-4}$

解析：

方法一

A 选项：当 $\ce{pH = 4}$ 时，相当于 $c(\ce{H+}) = \pu{10^-4 mol*L-1} = \pu{10E-5 mol*L-1}$，由图可得，此时 $c^2(\ce{M+}) = \pu{7.5E-8 mol*L-1}$，所以 $c(\ce{M+}) = \pu{\sqrt{7.5} \times 10^{-4} mol*L-1} < \pu{3E-4 mol*L-1}$。
B 选项：当 $c(\ce{H+}) = 0$ 时，溶液中不存在「外加酸」，此时有 $\ce{MA(s) <=> M+(aq) + A-(aq)}$，$\ce{A-}$ 的水解可忽略不计（注意当外加酸不为 $0$ 时不可忽略不计）。所以 $c(\ce{M+}) \approx c(\ce{A-}) $，所以 $K_{sp}(\ce{MA}) = c(\ce{M+}) \times c(\ce{A-}) = c^2(\ce{M+}) = \pu{5E-8 mol*L-1}$。
C 选项：如果题目外加酸是 $\ce{HA}$，则根据 $\ce{MA(s) <=> M+(aq) + A-(aq)}$ 和 $\ce{HA <=> H+ + A-}$ 得到：当 $c(\ce{HA})$ 增大（即 $c(\ce{H+})$ 增大）时，$\ce{HA}$ 电离程度增大，所以 $c(\ce{A-})$ 增大，从而根据「同离子效应」使得 $\ce{MA}$ 的沉淀溶解平衡逆向移动，使得 $c(\ce{M+})$ 降低，但图像显示其升高，所以所加酸不是 $\ce{HA}$。而加入其他的酸一定带有酸根离子，所以溶液中的电荷守恒不是 $c(\ce{M+}) + c(\ce{H+}) = c(\ce{A-}) + c(\ce{OH-})$，即该式不成立。
D 选项：由于求的是 $K_a(\ce{HA})$，根据定义可知 $K_a(\ce{HA}) = \dfrac{c(\ce{H+})\cdot c(\ce{A-})}{c(\ce{HA})}$，所以当 $c(\ce{HA}) = c(\ce{A-})$ 时，$K_a(\ce{HA}) = c(\ce{H+})$。由于「外加酸」不是 $\ce{HA}$，$\ce{M+}$ 不存在水解，$\ce{A-}$ 存在水解，所以有物料守恒：$c(\ce{M+}) = c(\ce{HA}) + c(\ce{A-})$，当 $c(\ce{HA}) = c(\ce{A-})$ 时，$c(\ce{A-}) = \dfrac{1}{2}c(\ce{M+})$。结合选项 B 分析，从而得到 $K_{sp}(\ce{MA}) = c(\ce{M+}) \cdot c(\ce{A-}) = \dfrac{1}{2}c^2(\ce{M+}) = \pu{5.0E-8}$，所以 $c^2(\ce{M+}) = \pu{10E-8 mol*L-1} $。根据图像可得，此时 $c(\ce{H+}) = \pu{20E-5 mol*L-1} = \pu{2E-4 mol*L-1}$，即 $K_a(\ce{HA}) = \pu{2E-4}$。

方法二

说明：以下分析中 $K_{sp}$ 表示 $K_{sp}(\ce{MA})$，$K_a$ 表示 $K_a(\ce{HA})$。

A C 选项同方法一。

由于已知 $c^2(\ce{M+})\sim c(\ce{H+})$ 成线性关系，所以可设

\[c^2(\ce{M+}) = kc(\ce{H+}) + b \]

原题中通过外加酸不断加入氢离子，使得 $c(\ce{M+})$ 也不断升高，那么从宏观上有：

\[\ce{MA(s) + H+(aq) <=> HA(aq) + M+(aq)} \]

该反应的平衡常数

\[K = \dfrac{c(\ce{HA})\cdot c(\ce{M+})}{c(\ce{H+})} = \dfrac{c(\ce{HA})\cdot c(\ce{M+})\cdot c(\ce{A-})}{c(\ce{H+})\cdot c(\ce{A-})} = \dfrac{K_{sp}}{K_a} \]

根据解法一有物料守恒如下：

\[ { } c(\ce{M+}) = c(\ce{HA}) + c(\ce{A-}) \longrightarrow c(\ce{HA}) = c(\ce{M+}) - c(\ce{A-}) \]

代入 $K$ 的表达式中得到：

\[K = \dfrac{c(\ce{HA})\cdot c(\ce{M+})}{c(\ce{H+})} = \dfrac{[c(\ce{M+}) - c(\ce{A-})]\cdot c(\ce{M+})}{c(\ce{H+})} = \dfrac{c^2(\ce{M+}) - c(\ce{M+})\cdot c(\ce{A-})}{c(\ce{H+})} = \dfrac{c^2(\ce{M+}) - K_{sp}}{c(\ce{H+})} \]

所以

\[\dfrac{c^2(\ce{M+}) - K_{sp}}{c(\ce{H+})} = \dfrac{K_{sp}}{K_a} \longrightarrow c^2(\ce{M+}) = \dfrac{K_{sp}}{K_a} c(\ce{H+}) + K_{sp} \longrightarrow \begin{cases} k = \dfrac{K_{sp}}{K_a}\\ b = K_{sp} \end{cases} \]

观察图像有：

\[\begin{cases} K_{sp} = b = \pu{5.0E-8}\\ \dfrac{K_{sp}}{K_a} = k = \dfrac{\pu{(7.5-5.0)\times 10^{-8}}}{\pu{10E-5}} \end{cases} \Longrightarrow \begin{cases} K_{sp} = \pu{5.0E-8}\\ K_a = \pu{2.0E-4} \end{cases} \]

可得到 BD 选项正确。

易错点及注意事项

题目若告诉某种离子浓度的 $-\lg$ 值为 $x$，说明该离子浓度为 $\pu{10^{-x} mol*L-1}$。
一般离子浓度若小于 $\pu{10^-5 mol*L-1}$ 视为完全沉淀。
两杯体积均为 $\pu{1L}$ 的溶液混合，得到的新溶液中各种离子的浓度是原来的一半。

沉淀滴定曲线图

例题

例（2022 湖南）：室温时，用 $\pu{0.100 mol*L-1}$ 的标准 $\ce{AgNO3}$ 溶液滴定 $\pu{15.00 mL}$ 浓度相等的 $\ce{Cl- 、Br-}$ 和 $\ce{I-}$ 混合溶液，通过电位滴定法获得 $\lg c(\ce{Ag+})$ 与 $V(\ce{AgNO3})$ 的关系曲线如图所示[忽略沉淀对离子的吸附作用。若溶液中离子浓度小于 $\pu{1.0E-5 mol*L-1}$，认为该离子沉淀完全。$K_{sp}(\ce{AgCl}) = \pu{1.8E-10},K_{sp}(\ce{AgBr}) = \pu{5.4E-13},K_{sp} = \pu{8.5E-17}$]。下列说法正确的是：

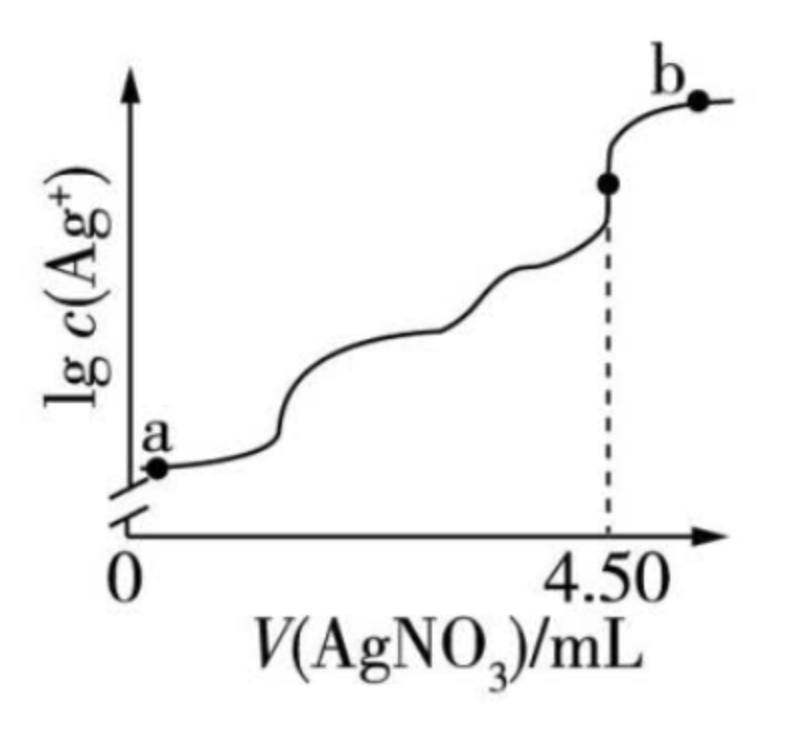
A. $a$ 点：有白色沉淀生成

B. 原溶液中 $\ce{I-}$ 的浓度为 $\pu{0.100 mol*L-1}$。

C. 当 $\ce{Br-}$ 沉淀完全时，已经有部分 $\ce{Cl-}$ 沉淀。

D. $b$ 点：$c(\ce{Cl-}) > c(\ce{Br-}) > c(\ce{I-}) > c(\ce{Ag+})$

解析：

A 选项：由图可知，整个滴定过程中一共产生了三次沉淀，又由于 $K_{sp}:\ce{AgCl > AgBr > AgI}$，所以 $\ce{AgI}$ 先沉淀，由于 $\ce{AgI}$ 是红色沉淀（$\ce{AgBr}$ 是浅黄色沉淀，$\ce{AgCl}$ 是白色沉淀），所以 $a$ 点应该是由黄色沉淀产生。
B 选项：由图可知，溶液第三次沉淀时，加入的 $\ce{AgNO3}$ 是 $\pu{4.5 mL}$，又由于 $\ce{Cl- 、Br-}$ 和 $\ce{I-}$ 浓度相等，根据沉淀顺序可知当 $\ce{AgI}$ 恰好完全沉淀时，$V(\ce{AgNO3}) = \pu{1.5 mL}$，根据此时 $n(\ce{Ag+}) = n(\ce{I-})$，那么有 $0.1 \times \pu{1.5E-3} = c(\ce{I-})\times \pu{15E-3}$，可以得到 $c(\ce{I-}) = \pu{0.01 mol*L-1}$。
C 选项：当 $\ce{Br-}$ 沉淀完全时，根据题意可知，此时 $c(\ce{Br-}) = \pu{1.0E-5 mol*L-1}$，根据 $K_{sp} = c(\ce{Ag+})\cdot c(\ce{Br-}) = \pu{5.4E-13}$，可计算得到 $c(\ce{Ag+}) = \pu{5.4E-8 mol*L-1}$，此时 $\ce{Cl-} = \pu{0.01 \times \dfrac{15}{18} mol*L-1}$ $Q(\ce{AgCl}) = c(\ce{Ag+})\cdot c(\ce{Cl-}) = \pu{4.5E-10}$，此时 $K_{sp}(\ce{AgCl}) = \pu{1.8E-10} < Q(\ce{AgCl})$，所以确实产生了 $\ce{Cl-}$ 沉淀。
D 选项：$b$ 点时 $\ce{AgNO3}$ 过量，所以此时 $c(\ce{Ag+})$ 最大。再根据三个沉淀的 $K_{sp}$ 可得 $c(\ce{Cl-}) > c(\ce{Br-}) >c(\ce{I-}) $。

易错点及注意事项

对于题目涉及到的「恰好沉淀一半」的问题，计算某离子浓度时，体积不是最开始的体积，需要用原物质的量除以新的体积。
对于沉淀溶解曲线图上的点，都满足 $K_{sp} = Q$。
利用 $\ce{AgNO3}$ 标准溶液滴定未知浓度的 $\ce{Cl-}$，一般用 $\ce{K2CrO4}$ 溶液作指示剂。

原因：根据计算可得，$\ce{AgCl}$ 的溶解度较小，先沉淀。又因为 $\ce{AgCl}$ 和 $\ce{Ag2CrO4}$ 沉淀颜色不同，所以当出现 $\ce{AgCl}$ 白色沉淀后，再滴入 $\ce{AgNO3}$，就会出现 $\ce{Ag2CrO4}$ 红棕色沉淀，说明 $\ce{AgCl}$ 已经完全沉淀。

判定：滴入最后半滴 $\ce{AgCl}$ 标准液，出现红棕色沉淀，且 $\pu{30s}$ 沉淀不消失，则达到沉淀平衡。

对数图像、分布分数图像分析

例题

例 1（2023 辽宁卷）：某废水处理过程中始终保持 $\ce{H2S}$ 饱和，即 $c(\ce{H2S}) = \pu{0.1 mol*L-1}$，通过调节 $\ce{pH}$ 使得 $\ce{Ni^2+}$ 和 $\ce{Cd^2+}$ 形成硫化物而分离，体系中 $\ce{pH}$ 与 $-\lg c$ 的关系如下图所示，$c$ 为 $\ce{HS- 、S^2-、Ni^2+}$ 和 $\ce{Cd^2+}$ 的浓度，单位为 $\pu{mol*L-1}$。已知 $K_{sp}(\ce{NiS}) > K_{sp}(\ce{CdS})$。下列说法正确的是（）

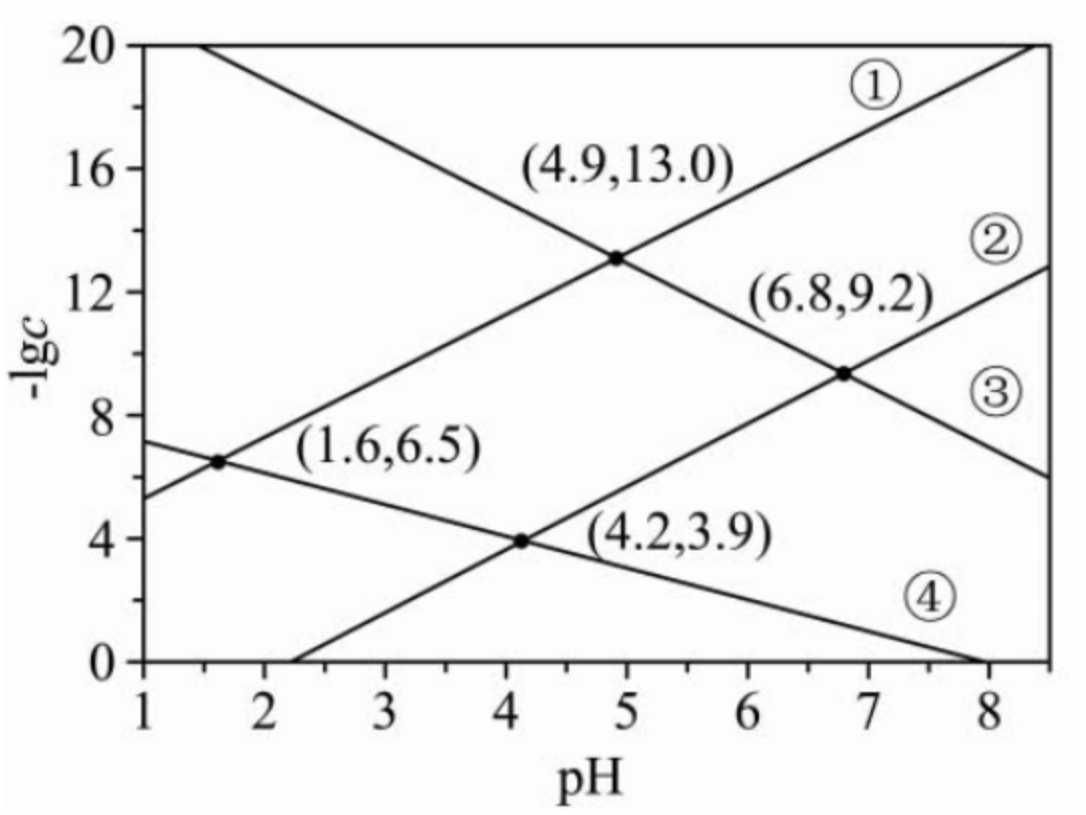
A. $K_{sp}(\ce{CdS}) =10^{-18.4}$

B. ③为 $\ce{pH}$ 与 $-\lg c(\ce{HS-})$ 的关系曲线

C. $K_{a_1}(\ce{H2S})= 10^{-8.1}$

D. $K_{a_2}(\ce{H2S}) = 10^{-14.7}$

解析：

由于纵轴表示 $-\lg c$，所以从下到上 $c$ 逐渐减小。

由 $\ce{H2S}$ 的两次电离得，随着 $\ce{pH}$ 的增大，$\ce{HS-}$ 和 $\ce{S^2-}$ 的浓度都逐渐增大，同时在 $\ce{pH}$ 较低时，$c(\ce{HS-})$ 更大，所以 ④ 是 $\ce{HS-}$ 曲线图，③ 是 $\ce{S^2-}$ 曲线图。

又有 $K_{sp}(\ce{NiS}) > K_{sp}(\ce{CdS})$ 得，同 $\ce{pH}$ 下，溶液中 $c(\ce{Ni^2+})$ 更大，所以 ① 表示 $\ce{Ni^2+}$ 曲线图，② 表示 $\ce{Cd^2+}$ 曲线图。

A 选项：根据图像可知，当 $c(\ce{Cd^2+}) = c(\ce{S^2-})$ 时，图像处于 $(4.9,13.0)$ 这个点，此时 $c(\ce{Cd^2+}) = c(\ce{S^2-}) = \pu{E-13 mol*L-1}$，所以 $K_{sp}(\ce{CdS}) = c(\ce{Cd^2+})\cdot c(\ce{S^2-}) = \pu{E-26} $。
B 选项：根据上述分析可知，B 错误。
C 选项：由图像可知，当 $\ce{pH} = 1.6$ 时，$c(\ce{H+}) = 10^{-1.6} ~\pu{mol*L-1}$，$c(\ce{HS-}) =10^{-6.5}~\pu{mol*L-1}$，此时 $K_{a_1}(\ce{H2S}) = \dfrac{c(\ce{H+})\cdot c(\ce{HS-})}{c(\ce{H2S})} = \dfrac{10^{-1.6}\times 10^{-6.5}}{10{-1}} = 10^{-7.1} $。
D 选项：由图像可知：

\[\begin{aligned} K_{a_1}(\ce{H2S})\times K_{a_2}(\ce{H2S}) &= \dfrac{c(\ce{H+})\cdot c(\ce{HS-})}{c(\ce{H2S})} \times \dfrac{c(\ce{H+})\cdot c(\ce{S^2-})}{c(\ce{HS-})} \\ &= \dfrac{c^2(\ce{H+})\cdot c(\ce{S^2-})}{c(\ce{H2S})} \\ &=\dfrac{\left(10^{-4.9}\right)^2\times \pu{E-13}}{\pu{E-1}} \\&= 10^{-21.8} \end{aligned} \]
根据 C 选项分析中得到的 $K_{a_1}(\ce{H2S})$，可计算得到 $K_{a_2}(\ce{H2S}) = 10^{-14.7}$。

例 2（2023 湖北卷）$\ce{H2L}$ 为某邻苯二酚类配体，其 $pK_{a_1} = 7.46$，$pK_{a_2} = 12.4$。常温下构建 $\ce{Fe(III) - H2L}$ 溶液体系，其中 $c_0(\ce{Fe^3+}) = \pu{2.0E-4 mol*L-1}$，$c_0(\ce{H2L}) = \pu{5.0E-3 mol*L-1}$。体系中含 $\ce{Fe}$ 物种的组分分布系数 $\delta$ 与 $\ce{pH}$ 的关系如图所示。分布分数 $\delta(x) = \dfrac{c(x)}{\pu{2.0E-4 mol*L-1}}$，已知 $\lg 2 \approx 0.30$，$\lg 3 \approx 0.48$。下列说法正确的是（）

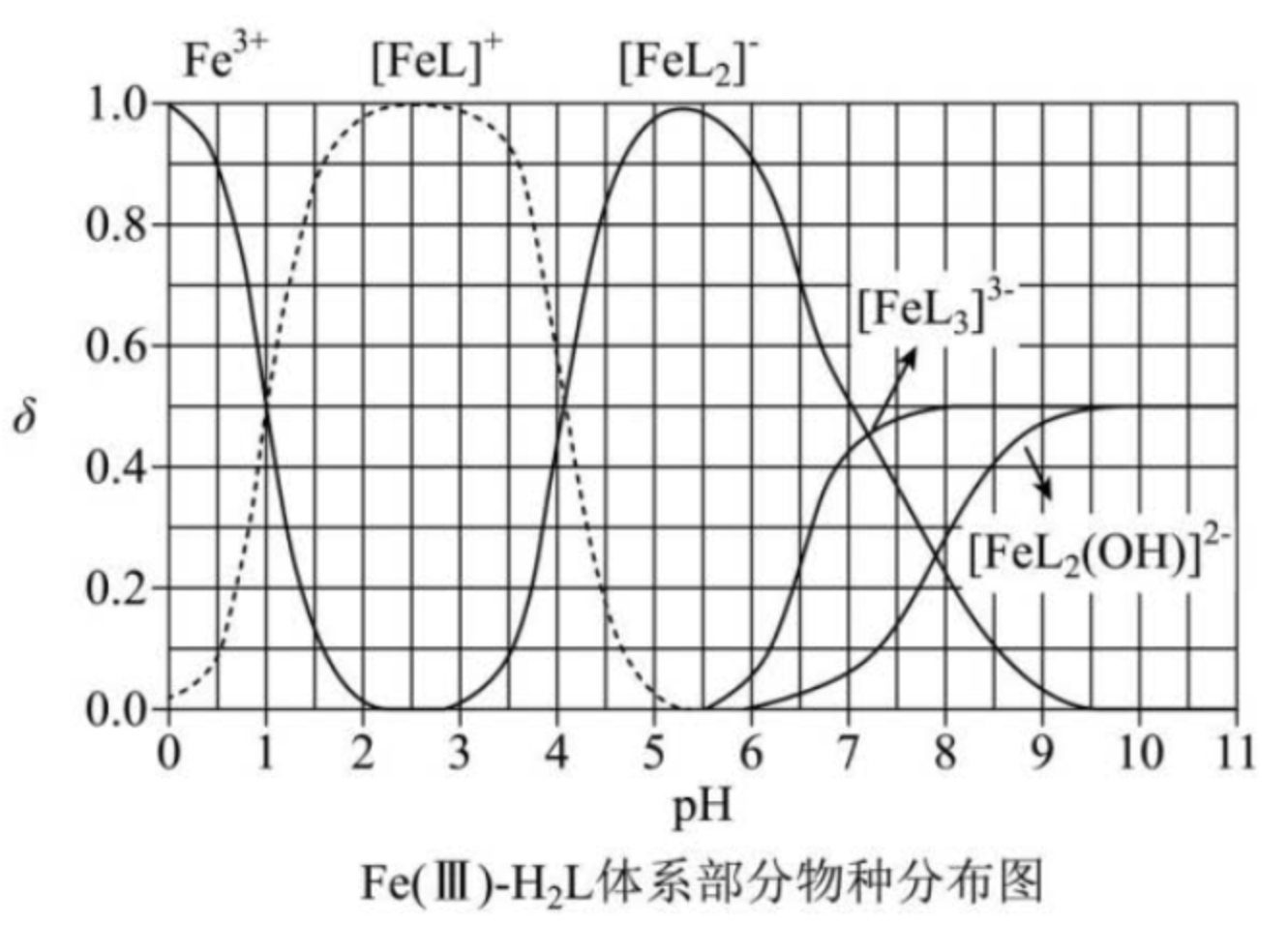
A. 当 $\ce{pH = 1}$ 时，体系中 $c(\ce{H2L}) > c(\ce{[FeL]+})> c(\ce{OH-}) > c(\ce{HL-})$

B. $\ce{pH}$ 在 $9.5 \sim 10.5$ 之间，含 $\ce{L}$ 的物种主要为 $\ce{L^2-}$

C. $\ce{L^2- + [FeL]+ <=> [FeL2]-}$ 的平衡常数的 $\lg K$ 约为 $14$

D. 当 $\ce{pH = 10}$ 时，参与配位的 $c(\ce{L^2-}) \approx \pu{1.0E-3 mol*L-1}$

解析：

A 选项：由图可知，当 $\ce{pH = 1}$ 时，$c(\ce{[FeL]+}) = 0.5\times \pu{2.0E-4 mol*L-1} = \pu{1.0E-4 mol*L-1}$，所以溶液中剩余的 $c(\ce{H2L}) = \pu{5.0E-3 - 1.0E-4 mol*L-1} = \pu{4.9E-3 mol*L-1}$。根据 $\ce{pH = 1}$ 可知此时 $c(\ce{H+}) = \pu{0.1 mol*L-1}$，所以对应 $c(\ce{OH-}) = \pu{E-13 mol*L-1}$。由题意可得 $K_{a_1} = \dfrac{c(\ce{H+})\cdot c(\ce{HL-})}{c(\ce{H2L})} = \dfrac{0.1 \times c(\ce{HL-})}{4.9\times 10^{-3}} = 10^{-7.46}$，可解得 $c(\ce{HL-}) \approx 4.9 \times 10^{-9.46}$。所以此时溶液中有 $c(\ce{H2L}) > c(\ce{[FeL]+}) > c(\ce{HL-}) > c(\ce{OH-})$。
B 选项：当 $\ce{pH}$ 在 $9.5\sim 10.5$ 之间时，根据图像可知，此时溶液中含铁离子主要是 $c(\ce{[FeL3]^3-}) = c(\ce{[FeL2(OH)]^2-}) = 0.5\times \pu{2.0E-4 mol*L-1} = \pu{1.0E-4 mol*L-1}$，所以其消耗的 $\ce{L^2-}$ 的浓度为 $\pu{3.0E-4 + 2.0E-4 = 5.0E-4 mol*L-1}$，所以此时溶液中剩余的 $c(\ce{H2L}) = \pu{5.0E-3 - 5.0E-4 = 4.5E-3 mol*L-1}$，画出此时 $\ce{H2L,HL- ,L^2-}$ 的分布分数图像如下：

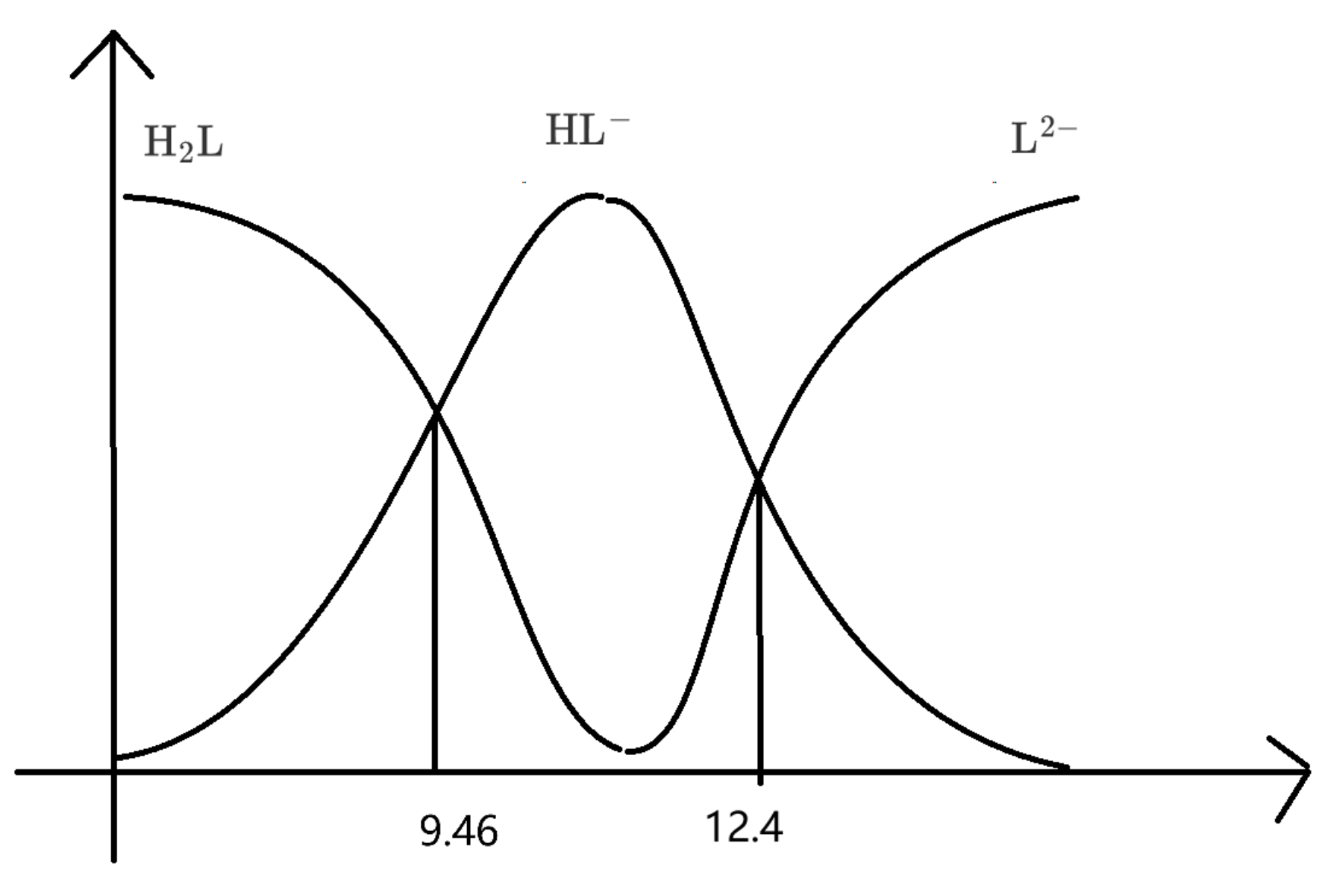
当 $\ce{pH}$ 在 $9.5\sim 10.5$ 之间时，大约位于图中两交点中点，此时几乎全为 $\ce{HL-}$，所以此时 $c(\ce{HL-})\approx \pu{4.5E-3 mol*L-1}$。所以含 $\ce{L}$ 的物种主要为 $\ce{HL-}$。
C 选项：由图可知，当 $c(\ce{[FeL2]-}) =c(\ce{[FeL]+})$ 时，$\ce{pH} \approx 4.1$，此时 $c(\ce{[FeL2]-}) = c(\ce{[FeL]+}) = 0.5 \times \pu{2.0E-4 mol*L-1} = \pu{1.0E-4 mol*L-1}$，消耗掉的 $\ce{L}$ 是 $\pu{2.0E-4 + 1.0E-4 = 3.0E-4 mol*L-1}$，$\ce{pH = 4.1}$ 时，根据 B 选项绘制的分布分数图像可知，主要以 $\ce{H2L}$ 为主，所以剩余的 $c(\ce{H2L}) = \pu{4.7E-3 mol*L-1}$，由于 $K_{a_1} \times K_{a_2} = \dfrac{c^2(\ce{H+})\cdot c(\ce{L^2-})}{c(\ce{H2L})}$，代入相关值可计算得到此时 $c(ce{L^2-}) = 4.7\times 10^{-14.66}~\pu{mol*L-1}$，又因为 $K = \dfrac{c(\ce{[FeL2]-})}{c(\ce{[FeL]+})\cdot c(\ce{L^2-}) } = \dfrac{1}{c(\ce{L^2-})}$，代入相关值并转化求得，$\lg K \approx 13.96 \approx 14$。
D 选项：由 B 选项分析可得，参与配位的 $c(\ce{L^2-}) \approx \pu{5.0E-4 mol*L-1}$。

关键点

弄清楚给定图像横纵坐标轴的浓度大小关系（从上往下是从小到大还是从大到小），学会利用图像进行分析，弄清每一个交点的化学意义。

易错点及注意事项

若给定图像坐标轴是 $-\lg c$，则从左到右，从上到下，$c$ 逐渐增大；反之，逐渐减小。
题目给定的 $\ce{Fe(III)}$ 指的是三价铁。
若一个物质同时存在 $K_{a_1}$ 和 $K_{a_2}$，若其中一个难以求解时，可以考虑求出另一个然后变形得到。

posted @ 2024-02-14 18:17 向日葵Reta 阅读(649) 评论(0) 编辑收藏举报

刷新页面返回顶部

得到 \(\ce{H+}\)	核心物质	失去 \(\ce{H+}\)（得到 \(\ce{OH-}\)）
\(\ce{H+}\)	\(\ce{H2O}\)	\(\ce{OH-}\)
\(\ce{H2CO3}\)	\(\ce{HCO3-}\)	\(\ce{CO3^2-}\)

得到 \(\ce{H+}\)	核心物质	失去 \(\ce{H+}\)（得到 \(\ce{OH-}\)）
\(\ce{H+}\)	\(\ce{H2O}\)	\(\ce{OH-}\)
\(\ce{H2CO3}\)	\(\ce{HCO3-}\)	\(\ce{CO3^2-}\)
/	\(\ce{NH4+}\)	\(\ce{NH3.H2O}\)

向日葵Reta

xrk's blog

【文化课学习笔记】【化学】选必一：水溶液中的离子反应与平衡（下）

【化学】选必一：水溶液中的离子反应与平衡（下）

盐类水解

基本概念

盐类水解的影响因素

内因（决定因素）

外因

应用

电解质溶液三大守恒

电荷守恒

物料守恒（元素守恒）

质子守恒

单一盐溶液

混合溶液

电解质溶液易混淆题型

题型一：等浓度、等体积的酸 + 碱

题型二：常温时 \(\ce{pH}\) 之和等于 \(14\) 且等体积的酸 + 碱

题型三：溶液呈中性的相关问题

题型四：等浓度与等 \(\ce{pH}\)

题型五：盐类水解相关离子比较

溶液中的微粒关系

解题思路

解题技巧

经典酸碱中和滴定 \(\ce{pH - V}\) 图像分析

解题步骤

解题要点及注意事项

分布分数图像分析

物质的量分数与 \(\ce{pH}\) 图像

浓度之比的 \(\lg\) 值与 \(\ce{pH}\) 图像

沉淀溶解平衡

基本概念

影响因素

溶度积 \(K_{sp}\) 的概念与表达式

定义

表达式

意义

影响因素

应用

溶度积 \(K_{sp}\) 与溶解度

溶度积 \(K_{sp}\) 与离子积 \(Q\)

应用

沉淀的生成

沉淀的溶解

沉淀的转化

实际生活中的应用

平衡图像分析

沉淀滴定曲线图

对数图像、分布分数图像分析

公告