数据结构---->数组
数组(Arrays)
一、数组
1.1数组的定义
数组: 由一组名字相同、下标不同的n(n≥1)个相同数据类型的数据元素a0,a1,a2,...,an-1构成的占用一块地址连续的内存单元的有限集合
数组的处理比其它复杂的结构要简单
① 数组中各元素具有统一的类型;
② 数组元素的下标一般具有固定的上界和下界,即数组一旦被定义,它的维数和维界就不再改变。
③数组的基本操作比较简单,除了结构的初始化和销毁之外,只有存取元素和修改元素值的操作。
高级语言中的数组是顺序结构;此处的数组既可以是顺序的,也可以是链式结构。
1.2数组的顺序存储表示和实现
问题:计算机的存储结构是一维的,而数组一般是多维的,怎样存放?
解决办法:事先约定按某种次序将数组元素排成一列序列,然后将这个线性序列存入存储器中。
行优先顺序:存储时先按行从小到大的顺序存储,在每一行中按列号从小到大存储。
列优先顺序:存储时先按列从小到大的顺序存储,在每一列中按行号从小到大存储。
若规定好了次序,则数组中任意一个元素的存放地址便有规律可寻,可形成地址计算公式;约定的次序不同,则计算元素地址的公式也有所不同
无论规定行优先或列优先,只要知道以下三要素便可随时求出任一元素的地址
① 始结点的存放地址(即基地址)
② 维数和每维的上、下界;
③ 每个数组元素所占用的单元数
假如:每个元素占有c个存储单元
一维数组:
loc(ai)=loc(a1)+(i-1)*c
m*n的二维数组(共有m行,每行有n列)
loc(aij)=loc(a11)+[(i-1)*n+j-1]*c
三维数组R[p][m][n]:
LOC(i,j,k)= LOC(0,0,0) +(i*m*n +j*n+k) *c
N维数组的顺序存储表示
#define MAX_ARRAY_DIM 8 //假设最大维数为8
typedef struct{
ELemType *base; //数组元素基址
int dim; //数组维数
int *bound; //数组各维长度信息保存区基址
int *constants; //数组映像函数常量的基址
}Array;
二、矩阵的存储(二维数组)
2.1矩阵的存储
由于矩阵是由m行n列组成,逻辑上与二维数组相同,故通常用二维数组来做矩阵的存储结构。
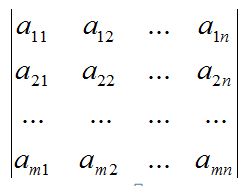
矩阵的运算:
1、矩阵相加 2、矩阵相间 3、矩阵相乘 4、矩阵转置5、矩阵求逆6、写数据7、读数据
2.2矩阵的传统转置

2.3矩阵乘法:
C=AB即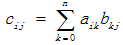
算法描述:
1、判断矩阵B的行、列是否等于A的列、行数
2、创建A的行数B的列数的矩阵C
3、计算C的元素值
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
for(int k=0;k<n;k++)
c[i][j]+=a[i][k]*b[k][j];
三、矩阵的压缩存储
特殊矩阵是指其中有许多值相同的元素或有许多零元素,且值相同的元素或零元素的分布有一定规律例如: 对称矩阵,三角矩阵,对角矩阵(所有非主对角线元素全等于零的n阶矩阵,称为对角矩阵或称为对角方阵。)
如果在矩阵中有许多值相同的元素或者是零元素。为了节省存储空间,可以对这类矩阵进行压缩存储。所谓压缩存储是指:为多个值相同的元只分配一个存储空间;对零元不分配空间。
稀疏矩阵压缩存储的缺点:将失去随机存取功能
以三角矩阵为例
空间分配:对角线及对角线上(或下)的每一元素分配一个存储空间,对角线下(或上)的重复元素分配一个存储空间。
占存储空间数:n*(n+1)/2 +1。
假设以一维数组sa[n(n+1)/2]作为n阶对称A的存储结构


若a ij存储到Sa[k]中,则k与i,j 对应关系为:
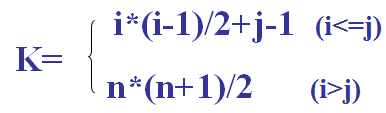
四、稀疏矩阵
稀疏矩阵:假设 m行n列的矩阵含t个非零元素,则称t/(m*n)为稀疏因子。通常认为 d £0.05的矩阵为稀疏矩阵且零值元素分布是随机的。
4.1稀疏矩阵的存储
4.1.1三元组表法
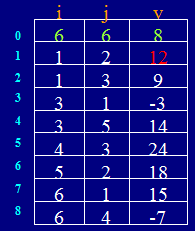
以下面的矩阵为例

三元组表线性表示
实现方法:将每个非零元素用一个三元组(i,j,aij)来表示,则每个稀疏矩阵可用一个三元组表来表示。如(( 1,2,12) ,(1,3,9), (3,1,-3), (3,5,14),(4,3,24), (5,2,18),(6,1,15), (6,4,-7))
三元组表矩阵表示
三元组矩阵表示(通常再加一行“总体”信息:即总行数、总列数、非零元素总个数)
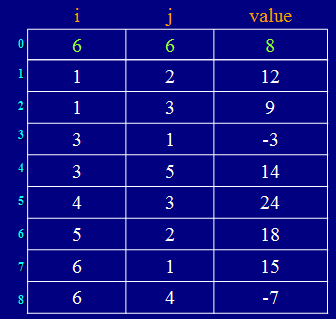
带辅助向量的三元组表示
在三元组矩阵表示的基础上增加2个辅助向量:
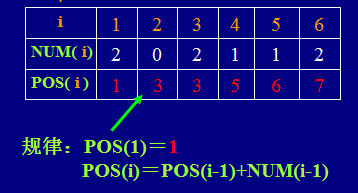
① 记录每行非0元素个数,用NUM(i)表示;
② 记录稀疏矩阵中每行第一个非0元素在三元组中的行号,用POS(i)表示。
一个结点的结构定义
public class Triple
{
private int i; //行号
private int j; //列号
private double value; //数值
}
整个三元组表的定义
public class TSMatrix {
privatefinalintMAXSIZE = 1000; // 数组的默认大小
privateintmu; // 行数
privateintnu; // 列数
privateinttu; // 矩阵中非零元素总个数
Triple[] data;// 三元组表,以行为主序存入一维向量 data[ ]中
}
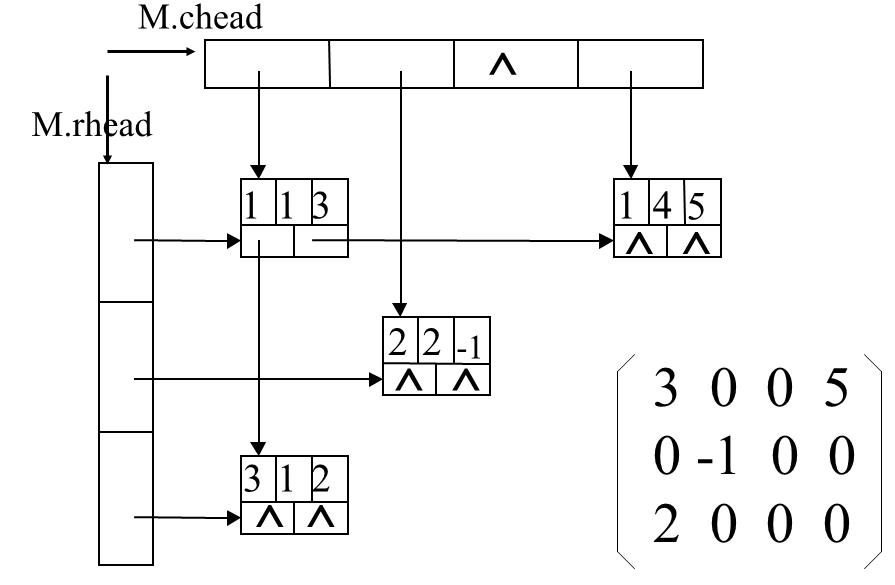
4.1.2十字链表
① 每行非零元素链接成带表头结点的链表;
② 每列非零元素也链接成带表头结点的链表。
则每个非零元素既是行循环链表中的一个结点;又是列循环链表中的一个结点,即呈十字链状。
4.2、稀疏矩阵的转置运算
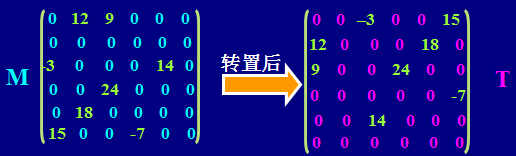
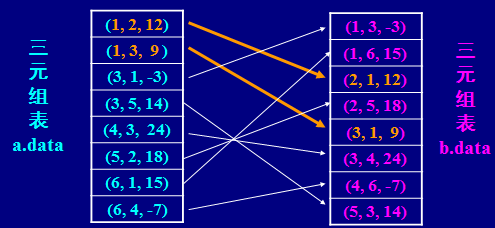
若采用三元组压缩技术存储稀疏矩阵,只要把每个元素的行下标和列下标互换,就完成了对该矩阵的转置运算,这种说法正确吗?
除了: (1)每个元素的行下标和列下标互换(即三元组中的i和j互换);
还应该: (2)转置后矩阵T的总行数和总列数与转置前矩阵M值不同(互换);
(3)重排三元组内元素顺序,使转置后的三元组也按行(或列)为主序有规律的排列
难点在(3)有以下两种实现方法
4.2.1压缩转置
思想:反复扫描a.data中的列序,从小到大依次进行转置。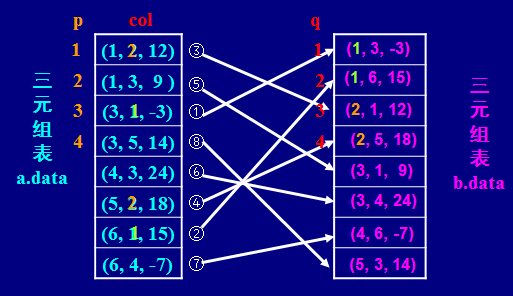
算法描述:

4.2.2(压缩)快速转置
思路:依次把a.data中的元素直接送入b.data的恰当位置上(即M三元组的p指针不回溯)。
关键:怎样寻找b.data的“恰当”位置?
设计思路:
如果能预知M矩阵每一列(即T的每一行)的非零元素个数,又能预知第一个非零元素在b.data中的位置,则扫描a.data时便可以将每个元素准确定位。
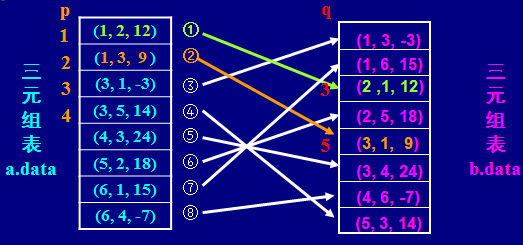
技巧:类比带辅助向量的三元组表,它正好携带每行(或列)的非零元素个数NUM(i)以及每行(或列)的第一个非零元素在三元组表中的位置POS(i)等信息。不过我们需要的是按列生成的M矩阵的辅助向量。
按列生成的M矩阵的辅助向量
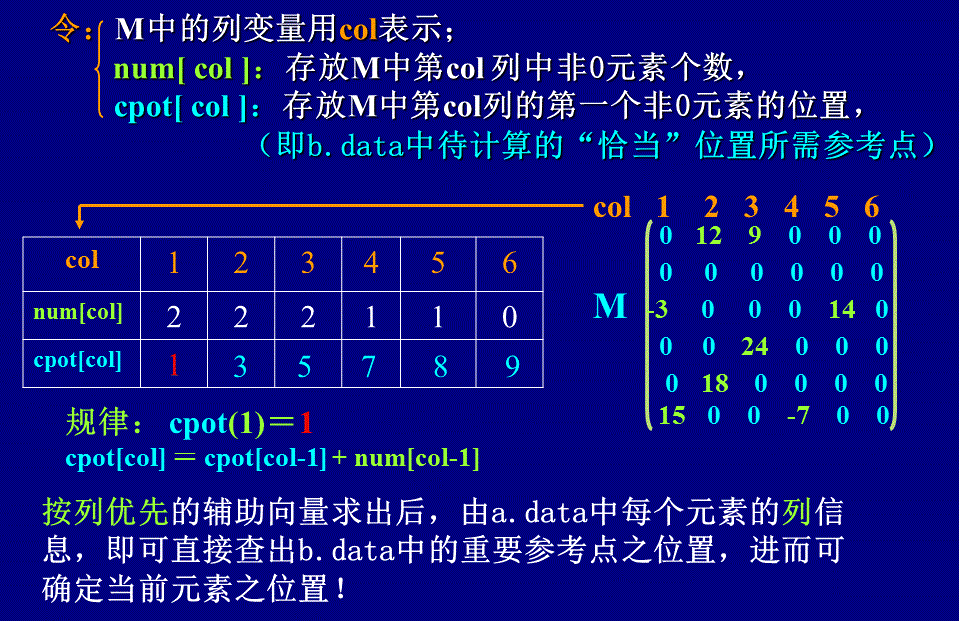
快速转置算法描述

效率比较:mu:行数 nu:列数tu:矩阵中非零元素总个数
传统转置:O(mu*nu)
压缩转置:O(mu*tu)
压缩快速转置:O(nu+tu)——牺牲空间效率换时间效率。



