图的着色问题
1、问题描述
图的m-着色判定问题——给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色,每个顶点着一种颜色,是否有一种着色法使G中任意相邻的2个顶点着不同颜色?
图的m-着色优化问题——若一个图最少需要m种颜色才能使图中任意相邻的2个顶点着不同颜色,则称这个数m为该图的色数。求一个图的最小色数m的问题称为m-着色优化问题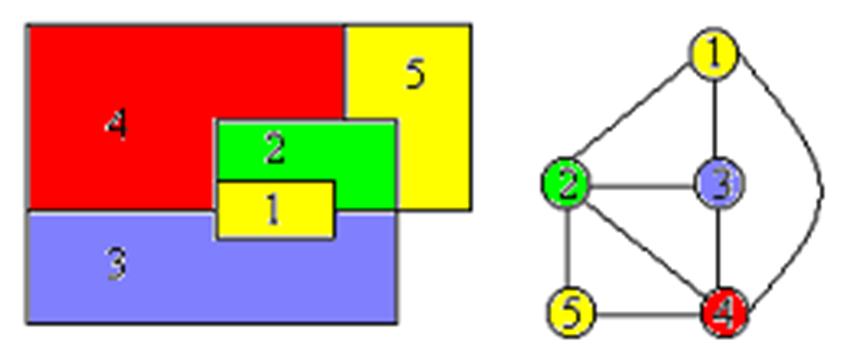
2、找一个图的所有m-着色方案
|
procedure MCOLORING( k )
∥这是图着色的一个递归回溯算法。图G 用它的布尔邻接矩阵GRAP H(1∶n , 1∶ n)表示∥
∥它计算并打印出符合以下要求的全部解, 把整数1 , 2 , ⋯ ,m 分配给图中∥
∥各个结点且使相邻近的结点的有不同的整数。k 是下一个要着色结点的下标∥
global integer m, n , X(1∶ n) boolean GRAPH (1∶n , 1∶n)
integer k
loop ∥产生对X( k)所有的合法赋值∥
call NEXTVALUE( k) ∥将一种合法的颜色分配给X( k) ∥
if X( k) = 0 then exit endif ∥没有可用的颜色了∥
if k = n
then print ( X) ∥至多用了m 种颜色分配给n 个结点∥
else call MCOLORING( k + 1 ) ∥所有m-着色方案均在此反复递归调用中产生∥
endif
repeat
end MCOLORING
|
在最初调用callMCOLORING(1)之前, 应对图的邻接矩阵置初值并对数组X置0值。在确定了X(1)到X(k-1)的颜色之后,过程NEXTVALUE从这m种颜色中挑选一种符合要求的颜色, 并把它分配给X(k) , 若无可用的颜色, 则返回X(k) = 0。
3、获取下一种颜色
|
procedure NEXTVALUE( k)
∥进入此过程前X(1) , ⋯ , X( k - 1 )已分得了区域[ 1 , m] 中的整数且相邻近的结点有不同的
整数。本过程在区域[0 ,m] 中给X( k )确定一个值:如果还剩下一些颜色, 它们与结点k 邻
接的结点分配的颜色不同, 就将其中最高标值的颜色分配给结点k ;如果没剩下可用的颜
色, 则置X( k) 为0∥
global integer m, n , X(1∶n) boolean GRAP H(1∶n , 1∶ n)
integer j , k
loop
X(k) ←(X(k) + 1 ) mod (m + 1) ∥试验下一个最高标值的颜色∥
if X( k ) = 0 then return endif ∥全部颜色用完∥
for j←1 to n do ∥检查此颜色是否与邻近结点的那些颜色不同∥
if GRAPH( k , j ) and ∥如果( k , j )是一条边∥
X(k) = X(j) ∥并且邻近的结点有相同的颜色∥
then exit endif
repeat
if j = n + 1 then return endif ∥找到一种新颜色∥
repeat ∥否则试着找另一种颜色∥
end NEXTVALUE
|
4、例子
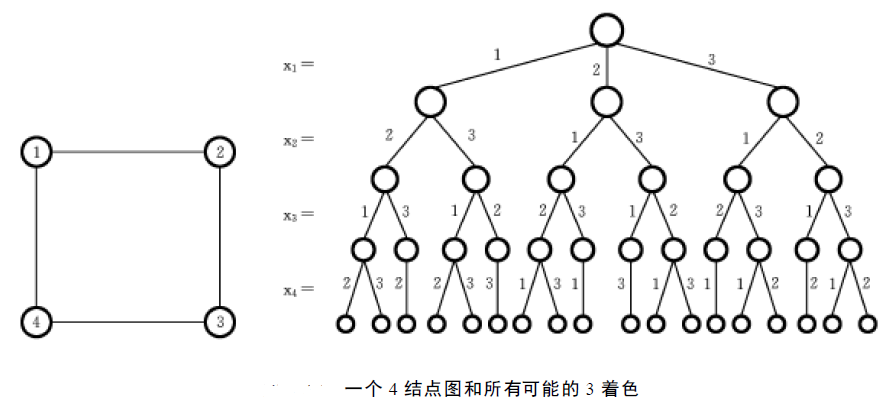




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律