动态规划---->最优二分检索树
最优二分检索树
最优二分检索树问题：求一棵使得预期成本最小的二分检索树
一、问题引出
或是一棵空树；或者是具有如下性质的非空二叉树：
（1）左子树的所有结点均小于根的值；
（2）右子树的所有结点均大于根的值；
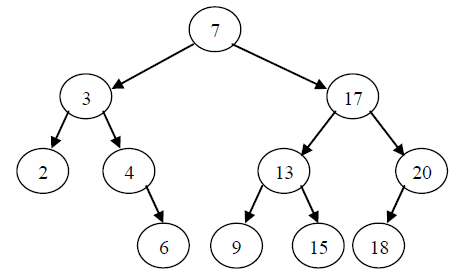
对于一个给定的标识符集合，可能有若干棵不同的二分检索树:
不同形态的二分检索树对标识符的检索性能是不同的。
设给定的标识符集合是{a1,a2,…,an}，并假定a1＜a2＜ … ＜ an。设，P(i)是对ai检索的概率，Q(i)是正被检索的标识符X恰好满足： ai＜X＜ai+1，0≤i≤n（设a0=-∞,an+1=+∞)时的概率，即一种不成功检索情况下的概率。
内结点：代表成功检索情况，刚好有n个
外结点：代表不成功检索情况，刚好有n＋1个
平均检索成本＝Σ每种情况出现的概率×该情况下所需的比较次数
平均检索成本的构成：成功检索成分＋不成功检索成分
●成功检索：在内结点终止的成功检索 P(i)*level(ai) ； 其中，level(ai)= 结点ai的级数=l
●不成功检索：外部结点的不成功检索的成本分担额为：Q(i)*(level(Ei)-1)
最优二分检索树问题：求一棵使得预期成本最小的二分检索树
二、问题分析
2.1、多阶段决策过程
把构造二分检索树的过程看成一系列决策的结果。
决策的策略：决策树根，如果{a1,a2,…,an}存在一棵二分检索树，ak是该树的根，则内结点a1,a2,…,ak-1和外部结点E0,E1,…,Ek-1将位于根ak的左子树中，而其余的结点将位于右子树中。
● 左、右子树的预期成本——左、右子树的根处于第一级
● 左、右子树中所有结点的级数相对于子树的根测定，而相对于原树的根少1
2.1、最优性原理成立
若T最优二分检索树，则COST(L)和COST(R)将分别是包含a1,a2,…,ak-1和E0,E1,…,Ek-1、及ak＋1, ak+2, …,an和Ek,Ek+1,…,En的最优二分检索(子)树。记由ai+1,ai+2,…,aj和Ei,Ei+!,…,Ej构成的二分检索树的成本为C(i,j)，则对于最优二分检索树T有，
COST(L) = C(0,k-1)
COST(R) = C(k,n)
C[i,j] 表示点i+1，i+2到点j所组成的最优解
W[i,j] 表示i-j所有节点的概率和，因为在左右子树添加一个根节点，导致左右子树的所有节点的深度增加了1，所以加上W[i,j]
三、最优检索树构建过程
四、例子
设n=4,且(a1,a2,a3,a4)=(do,if,read,while)。设P(1:4) = (3,3,1,1)，Q(0:4) = (2,3,1,1,1) (概率值“扩大”了16倍)
初始：W(i,i)=Q(i) C(i,i)=0 R(i,i)=0
1、计算W C R
2、计算结果
3、二分检索树：
T04=2 =>T01(左子树），T24(右子树） 即0到4以2为分界
T01=1 =>T00(左子树），T11(右子树）
T24=3 =>T22(左子树），T34(右子树）
4、树的形态
