静态查找---->顺序、折半、分块查找
一、基本概念
查找表
由同一类型的数据元素（或记录）构成的集合。
查 找
查询(Searching)特定元素是否在表中。
静态查找
只查找，不改变集合内的数据元素。
动态查找
既查找，又改变（增减）集合内的数据元素。
关键字
记录中某个数据项的值，可用来识别一个记录
主关键字
可以唯一标识一个记录的关键字
次关键字
识别若干记录的关键字
平均查找长度（average search length , ASL）
是为确定数据元素在查找表中的位置，需要和给定的值进行比较的关键字个数的期望值，称为查找算法在查找成功时的平均查找长度。
二、静态查找
2.1、顺序查找-------线性查找
顺序查找：即用逐一比较的办法顺序查找关键字，这显然是最直接的办法。
public class OrderSearch {
public static int ordersearch(int[] arry, int des) {
for (int i = 0; i < arry.length; i++) {
if (des == arry[i])
return i;
}
return -1;
}
public static void main(String[] args) {
int[] a = new int[] { 2, 6, 5, 6, 7, 3, };
System.out.println(ordersearch(a, 3));
}
}
技巧：把待查关键字key存入表头或表尾（俗称“哨兵”），这样可以加快执行速度。
算法的基本思想是：在查找表的一端设置一个称为“监视哨”的附加单元，存放要查找的数据元素关键字，其目的在于免去查找过程中每一步都检测整个表是否查找完毕。然后从表的另一端开始查找，如果在“监视哨”位置找到给定关键字，则失败，否则成功返回相应元素的位置。
ASL＝= (1+ 2 + … + n)/n = (n+1)/2=（1＋n）/2 ，时间效率为 O(n)
优点：算法简单，且对顺序结构或链表结构均适用。
缺点： ASL 太长，时间效率太低。
2.2、折半查找--------二分查找
折半查找又称为二分查找，这种查找方法需要待查的查找表满足两个条件：首先，查找表必须使用顺序的存储结构（树结构可借助二叉排序树来查找，属动态查找表形式）；其次，查找表必须按关键字大小有序排列。
算法的基本思想是：首先，将查找表中间位置数据元素的关键字与给定关键字比较，如果相等则查找成功；否则利用中间元素将表一分为二，如果中间元素关键字大于给定关键字，则在前一子表中进行折半查找，否则在后一子表中进行折半查找。重复以上过程，直到找到满足条件的元素，则查找成功；或直到子表为空为止，即查找范围的上界≤下界时停止查找，此时查找不成功。
例子：
（05 13 19 21 37 56 64 75 80 88 92）
① 先设定3个辅助标志: low指向待查元素所在区间的下界，high指向待查元素所在区间的上界,mid指向待查元素所在区间的中间位置，
② 运算步骤：
(1) 上例中low =1,high =11 ,mid =6 ，待查范围是 [1,11]；
(2) 若 ST.elem[mid].key < key，说明 key∈[mid+1,high] ，则令：low =mid+1;重算
(3) 若 ST.elem[mid].key > key，说明key∈[low ,mid-1]， 则令：high =mid–1;重算 mid ；
(4) 若 ST.elem[ mid ].key = key，说明查找成功，元素序号=mid;
结束条件： （1）查找成功 ： ST.elem[mid].key = key
（2）查找不成功 ： high≤low （意即区间长度小于0）
算法的实现
public int binSearch(int array[], int k) {
int low = 0;
int high = array.length - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (array[mid] == k)
return mid;
else if (array[mid] < k)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
二分查找的效率（ASL）
1次比较就查找成功的元素有1个（20），即中间值；
2次比较就查找成功的元素有2个（21），即1/4处（或3/4）处；
3次比较就查找成功的元素有4个（22），即1/8处（或3/8）处…
4次比较就查找成功的元素有8个（23），即1/16处（或3/16）处…
则第h次比较时查找成功的元素会有（2h-1）个；
则第h+1次比较时查找成功的元素会有（2h）个；
为方便起见，假设表中全部n个元素＝ 2h+1-1个（也就是上面所有比较次数的和，此时就不用讨论第h+1次比较后还有剩余元素的情况了）
假设表的长度n =2h+1-1，
2.3、分块查找------索引顺序查找
这是一种顺序查找的另一种改进方法。
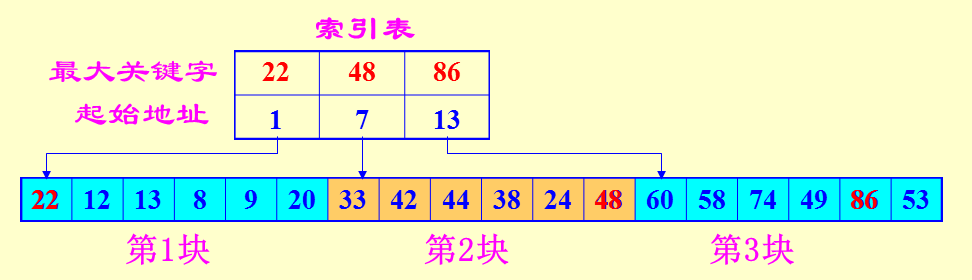
先让数据分块有序，即分成若干子表，要求每个子表中的数值（用关键字更准确）都比后一块中数值小（但子表内部未必有序）。然后将各子表中的最大关键字构成一个索引表，表中还要包含每个子表的起始地址（即头指针）。
特点：块间有序，块内无序
① 对索引表使用折半查找法（因为索引表是有序表）；
② 确定了待查关键字所在的子表后，在子表内采用顺序查找法（因为各子表内部是无序表）；
效率：
