动态查找---->平衡二叉树（AVL树）
平衡二叉树（AVL）
一、 平衡二叉树
在二叉查找树T中，若所有结点的平衡因子的绝对值均不超过1，则称T为一棵AVL树。
平衡二叉树又称AVL树，它是具有如下性质的二叉树：
• 左、右子树是平衡二叉树；
• 所有结点的左、右子树深度之差的绝对值≤ 1
为了方便起见，给每个结点附加一个数字，给出该结点左子树与右子树的高度差。这个数字称为结点的平衡因子balance。这样，可以得到AVL树的其它性质：
• 任一结点的平衡因子只能取：-1、0或 1；如果树中任意一个结点的平衡因子的绝对值大于1，则这棵二叉树就失去平衡，不再是AVL树；；
•对于一棵有n个结点的AVL树，其高度保持在O(log2n)数量级，ASL也保持在O(log2n)量级。
二、 平衡调整----旋转
如果在一棵AVL树中插入一个新结点，就有可能造成失衡，此时必须重新调整树的结构，使之恢复平衡。我们称调整平衡过程为平衡旋转。无论是右旋还是左旋，都不改变二叉树的中序遍历结果。
1. 右旋（顺时针方向旋转）
结点v 是结点p 的左孩子，X和Y分别是v 的左、右子树，Z为p的右子树。所谓围绕结点p 的右旋操作，就是重新调整这些结点位置，将p作为v 的右孩子，将X 作为v 的左子树，将Y和Z分别作为p的左、右子树。围绕p右旋的结果。
2. 左旋（逆时针方向旋转）
结点v 是结点p 的右孩子，Y 和Z 分别是v的左、右子树，X 为p 的左子树。所谓围绕结点p 的左旋操作，就是将p 作为v 的左孩子，将Z 作为v 的右子树，将X 和Y 分别作为p 的左、右子树。围绕p左旋的结果如图所示。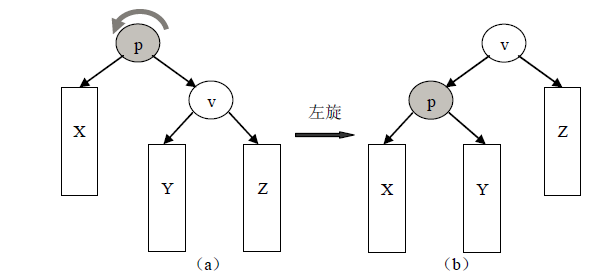
三、 插入操作
一般的，若在插入新的结点x 之后AVL 树T失去平衡，则失去平衡的结点只可能是x的祖先，且层次数小于等于x 的祖父的结点；也就是说失去平衡的结点是从x 的祖父到根的路径上的结点，但这些结点并不都是失去平衡的结点，有些结点仍然可能是平衡的。为了修正失衡的现象，可以从结点x 出发逆行向上，依次检查x 祖先的平衡因子，找到第一个失衡的祖先结点g。在从x 到g 的路径上，假设p 为g 的孩子结点，v 为p 的孩子结点。有结点p、v 必不为空，p 至少是x 的父亲，v 至少是x 本身。结点g、p、v 之间的父子关系共有4 种不同的组合，以下根据这4 种不同的组合，通过对结点g、p的旋转，使这一局部恢复平衡。
平衡旋转可以归纳为四类：
- LL平衡旋转
- RR平衡旋转
- LR平衡旋转
- RL平衡旋转
1）LL平衡旋转： p 是g的左孩子，且v是p的左孩子；
在这种情况下，必定是由于在v 的后代中插入了新结点x 而使得g不再平衡。针对这种情况，可以简单的通过结点g 的单向右旋，即可使得以g为根的子树得到平衡
2）RR平衡旋转： p是g的右孩子，且v 是p的右孩子；
与第一种情况对称，此时，失衡是由于在g 的右孩子的右子树中插入结点x造成的。在这种情况下需要通过结点g 的单向左旋来完成局部的平衡。
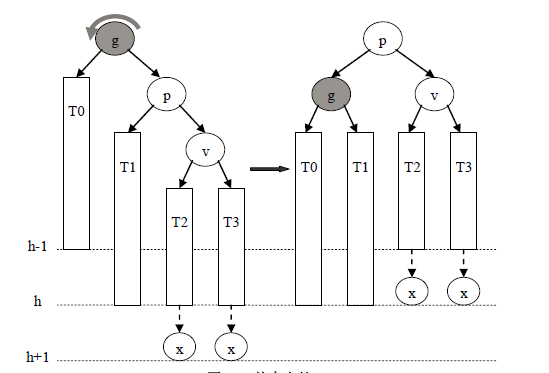
3）LR平衡旋转： p是g的左孩子，且v是p的右孩子；
如果是在p 的左孩子的右子树中插入一个结点，则对应为第三种情况。在这种情况中，要使得局部的失衡重新平衡，那么需要先后进行先左后右的双向旋转：第一次是结点p的左旋，第二次是结点g 的右旋。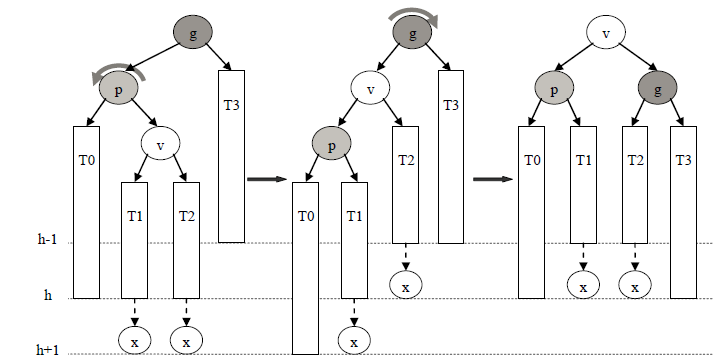
4）RL平衡旋转：
p是g的右孩子，且v是p的左孩子；第四种情况与第三种情况对称，其平衡调整过程也与第三种情况对称，可以通过先右后左的双向旋转来完成，其中第一次是结点p 的右旋，第二次是结点g的左旋。
四、 删除节点
按照通常的二叉查找树删除结点的方法在AVL树中删除结点x之后，如果发生失衡现象，为了重新平衡，同样从x出发逆行向上找到第一个失衡的结点g，通过旋转操作实现AVL树的重新平衡。使得结点g失衡的原因可以看成四种：
1. 失衡是由于 g 的左孩子的左子树过高造成的；
2. 失衡是由于 g 的右孩子的右子树过高造成的；
3. 失衡是由于 g 的左孩子的右子树过高造成的；
4. 失衡是由于 g 的右孩子的左子树过高造成的。
这四种情况与插入结点导致失衡的四种情况进行平衡化的旋转方法相同。但是需要注意两个特殊情况：失衡可能是由于左（右）孩子的左、右子树同时过高造成的，
五、 旋转操作的统一实现方法
前面介绍的4 种平衡旋转操作，需要根据结点g、p、v（p是g的孩子，v是p的孩子）之间的相互关系来判断应该使用的旋转方法。为此，在这里引入一种统一的算法，这种实现简洁、直观，容易实现。
在插入或删除结点x 之后，从x出发逆行向上，找到第一个失衡的结点g，然后根据g失衡的原因,设置p和v的指向，p 和v都是其父结点较高子树的根。此时，在这一局部，以p的兄弟为根有一棵子树，即g 较矮的子树；以v的兄弟为根有一棵子树，即p较矮的子树；v有两棵子树；一共有4棵子树。注意，在这4棵子树中可能有空树。显然，以失衡结点g 为根的局部平衡是在这3 个结点和4棵子树间完成的。
在确定了这3 个结点和4棵子树之后，接着为它们重命名。具体的命名方法是，从左到右将4 棵子树命名为T0、T1、T2、T3；按照中序顺序将结点g、p、v 分别命名为a、b、c。
四种不同旋转情况的命名见图所示。
一旦完成重命名，无论对于那种情况，我们都能以相同的方法将这3 个结点和4棵子树重新组合起来，以达到旋转平衡的目的。如图（e）所示，以结点b作为局部子树的根，结点a 和c 分别是b 的左孩子和右孩子，结点a 的左右子树分别是T0、T1，结点c的左右子树分别是T2、T3。
算法rotate
输入：失衡的结点z
输出：平衡后子树的根结点
private BinTreeNode rotate(BinTreeNode z) {
BinTreeNode y = higherSubT(z); // 取y为z更高的孩子
BinTreeNode x = higherSubT(y); // 取x为y更高的孩子
boolean isLeft = z.isLChild(); // 记录：z是否左孩子
BinTreeNode p = z.getParent(); // p为z的父亲
BinTreeNode a, b, c; // 自左向右，三个节点
BinTreeNode t0, t1, t2, t3; // 自左向右，四棵子树
// 以下分四种情况
if (y.isLChild()) { // 若y是左孩子，则
c = z;
t3 = z.getRChild();
if (x.isLChild()) { // 若x是左孩子(左左失衡)
b = y;
t2 = y.getRChild();
a = x;
t1 = x.getRChild();
t0 = x.getLChild();
} else { // 若x是右孩子(左右失衡)
a = y;
t0 = y.getLChild();
b = x;
t1 = x.getLChild();
t2 = x.getRChild();
}
} else { // 若y是右孩子，则
a = z;
t0 = z.getLChild();
if (x.isRChild()) { // 若x是右孩子(右右失衡)
b = y;
t1 = y.getLChild();
c = x;
t2 = x.getLChild();
t3 = x.getRChild();
} else { // 若x是左孩子(右左失衡)
c = y;
t3 = y.getRChild();
b = x;
t1 = x.getLChild();
t2 = x.getRChild();
}
}
// 摘下三个节点
z.sever();
y.sever();
x.sever();
// 摘下四棵子树
if (t0 != null)
t0.sever();
if (t1 != null)
t1.sever();
if (t2 != null)
t2.sever();
if (t3 != null)
t3.sever();
// 重新链接
a.setLChild(t0);
a.setRChild(t1);
c.setLChild(t2);
c.setRChild(t3);
b.setLChild(a);
b.setRChild(c);
// 子树重新接入原树
if (p != null)
if (isLeft)
p.setLChild(b);
else
p.setRChild(b);
return b;// 返回新的子树根
}
AVL 树也是一棵二叉查找树，则AVL 树的实现可以通过继承二叉查找树来实现。AVL树与一般二叉查找树不同的是，在插入和删除结点之后需要重新进行平衡。因此，只需要重写insert 和remove 方法即可。
附：整个的avl树的代码
package dsa.adt;
import dsa.strategy.Strategy;
public class AVLTree extends BSTree {
public AVLTree() {
super();
}
public AVLTree(Strategy strategy) {
super(strategy);
}
private boolean isBalance(BinTreeNode v) {
if (v == null)
return true;
int lH = (v.hasLChild()) ? v.getLChild().getHeight() : -1;
int rH = (v.hasRChild()) ? v.getRChild().getHeight() : -1;
return (Math.abs(lH - rH) <= 1);
}
private BinTreeNode higherSubT(BinTreeNode v) {
if (v == null)
return null;
int lH = (v.hasLChild()) ? v.getLChild().getHeight() : -1;
int rH = (v.hasRChild()) ? v.getRChild().getHeight() : -1;
if (lH > rH)
return v.getLChild();
if (lH < rH)
return v.getRChild();
if (v.isLChild())
return v.getLChild();
else
return v.getRChild();
}
private BinTreeNode rotate(BinTreeNode z) {
BinTreeNode y = higherSubT(z); // 取y为z更高的孩子
BinTreeNode x = higherSubT(y); // 取x为y更高的孩子
boolean isLeft = z.isLChild(); // 记录：z是否左孩子
BinTreeNode p = z.getParent(); // p为z的父亲
BinTreeNode a, b, c; // 自左向右，三个节点
BinTreeNode t0, t1, t2, t3; // 自左向右，四棵子树
// 以下分四种情况
if (y.isLChild()) { // 若y是左孩子，则
c = z;
t3 = z.getRChild();
if (x.isLChild()) { // 若x是左孩子(左左失衡)
b = y;
t2 = y.getRChild();
a = x;
t1 = x.getRChild();
t0 = x.getLChild();
} else { // 若x是右孩子(左右失衡)
a = y;
t0 = y.getLChild();
b = x;
t1 = x.getLChild();
t2 = x.getRChild();
}
} else { // 若y是右孩子，则
a = z;
t0 = z.getLChild();
if (x.isRChild()) { // 若x是右孩子(右右失衡)
b = y;
t1 = y.getLChild();
c = x;
t2 = x.getLChild();
t3 = x.getRChild();
} else { // 若x是左孩子(右左失衡)
c = y;
t3 = y.getRChild();
b = x;
t1 = x.getLChild();
t2 = x.getRChild();
}
}
// 摘下三个节点
z.sever();
y.sever();
x.sever();
// 摘下四棵子树
if (t0 != null)
t0.sever();
if (t1 != null)
t1.sever();
if (t2 != null)
t2.sever();
if (t3 != null)
t3.sever();
// 重新链接
a.setLChild(t0);
a.setRChild(t1);
c.setLChild(t2);
c.setRChild(t3);
b.setLChild(a);
b.setRChild(c);
// 子树重新接入原树
if (p != null)
if (isLeft)
p.setLChild(b);
else
p.setRChild(b);
return b;// 返回新的子树根
}
private BinTreeNode reBalance(BinTreeNode v) {
if (v == null)
return root;
BinTreeNode c = v;
while (v != null) { // 从v开始，向上逐一检查z的祖先
if (!isBalance(v))
v = rotate(v); // 若v失衡，则旋转使之重新平衡
c = v;
v = v.getParent(); // 继续检查其父亲
}// while
return c;
}
// 按关键字插入元素ele
public void insert(Object ele) {
super.insert(ele);
root = reBalance(startBN);
}
// 若查找表中存在与元素ele关键字相同元素，则删除一个并返回；否则，返回null
public Object remove(Object ele) {
Object obj = super.remove(ele);
root = reBalance(startBN);
return obj;
}
}
