数据结构---->图的存储结构
树的存储结构
2.1邻接矩阵(数组)表示法
图没有顺序映像的存储结构,但可以借助数组来表示数据元素之间的关系。
建立一个顶点表(记录各个顶点信息)和一个邻接矩阵(表示各个顶点之间关系)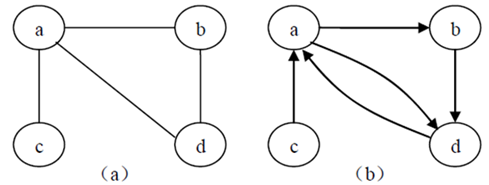
顶点表:(a,b,c,d)
邻接矩阵:
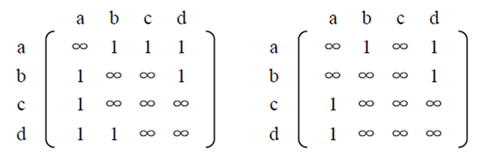
分析1:无向图的邻接矩阵是对称的;
分析2:顶点i 的度=第i 行 (列) 中1 的个数;
特别:完全图的邻接矩阵中,对角元素为0,其余全1。
有向带权图和它的邻接矩阵:
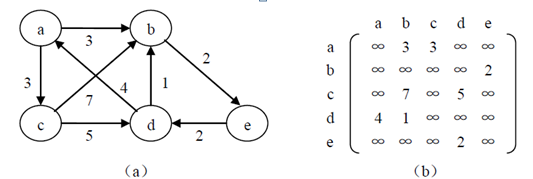
分析1:有向图的邻接矩阵可能是不对称的。
分析2:顶点的出度=第i行元素之和,OD( Vi )=∑A.Edge[ i ][j ]
顶点的入度=第i列元素之和。ID( Vi )=∑A.Edge[ j ][i ]
顶点的度=第i行元素之和+第i列元素之和,即:TD(Vi)=OD( Vi )+ ID( Vi )
邻接矩阵法优点:容易实现图的操作,如:判断顶点之间是否有边(弧)、找顶点的邻接点等等。
邻接矩阵法缺点:首先n个顶点需要N×N个单元存储边(弧);空间效率为O(n2)。对稀疏图而言尤其浪费空间。其次,矩阵结构是静态的,其大小N需要预先估计,然后创建的矩阵。然而,图的规模往往是动态变化的,N的估计过大会造成更多的空间浪费,如果估计过小则经常会出现空间不够用的情况。
2.2、邻接表(链式)表示法
邻接矩阵的空间效率之所以低,是因为其中大量的单元所对应的边有可能并未在图中出现,这是静态数组结构不可避免的问题。既然如此,则可以将静态的存储结构改为动态的链式存储结构。按照这一思路可以得到图的另一种表示形式,它其实是对邻接矩阵法的一种改进,即邻接表。
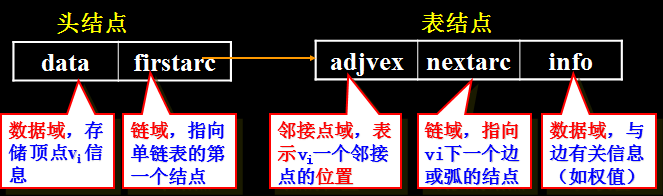
每个单链表附设一个头结点(设为2个域),存vi信息;
每个单链表的头结点用顺序存储结构存储。
对每个顶点vi 建立一个单链表,把与vi有关联的边的信息(即度或出度边)链接起来,表中每个结点都设为3个域;
无向图的邻接表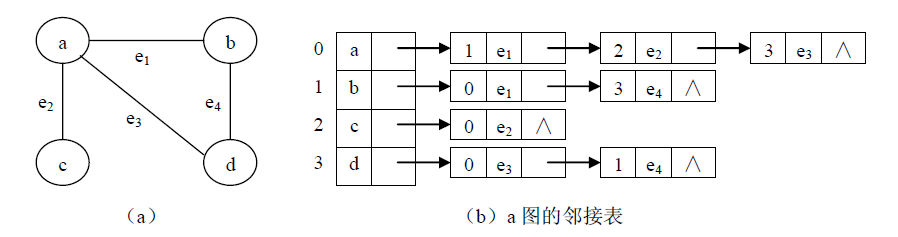
对于n个顶点e条边的无向图,邻接表中除了n个头结点外,只有2e个表结点,空间效率为O(n+2e)。若是稀疏图(e<<n2),则比邻接矩阵表示法O(n2)省空间。
顶点vi的度恰为顶点vi的邻接表中边表结点的个数;
有向图的邻接表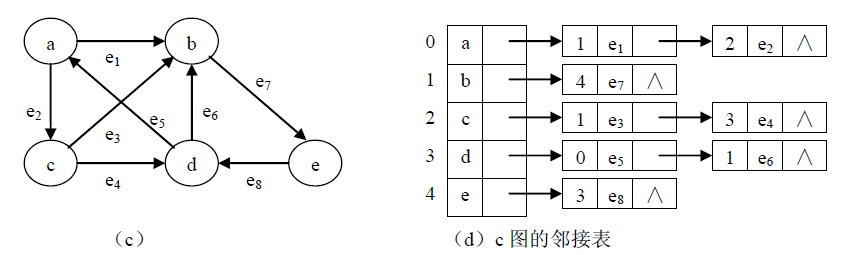
在有向图中,邻接表中除了n个头结点外,只有e个表结点,空间效率为O(n+e)。若是稀疏图,则比邻接矩阵表示法合适。
顶点vi的邻接表中边表结点的个数仅为顶点vi的出度,为求顶点vi的入度必须遍历整个邻接表。在所有链表中其邻接点域的值指向vi的位置的结点个数是顶点vi的入度。
逆邻接表:为了方便求得有向图中顶点的入度,可以建立一个有向图的逆邻接表。
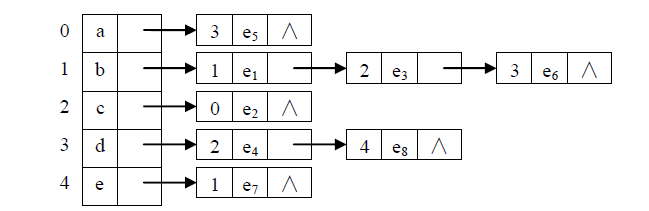
邻接表的优点:空间效率高;容易寻找顶点的邻接点;
邻接表的缺点:判断两顶点间是否有边或弧,需搜索两结点对应的单链表,没有邻接矩阵方便。
邻接表与邻接矩阵联系:邻接表中每个链表对应于邻接矩阵中的一行,链表中结点个数等于一行中非零元素的个数。
用途:邻接矩阵多用于稠密图的存储(e接近n(n-1)/2);而邻接表多用于稀疏图的存储(e<<n2)
2.3 双链式存储结构
虽然邻接表是图的一种很有效的存储结构,在邻接表中容易求得顶点和边的各种信息。但是这种结构会给图的某些操作带来不便。例如,在无向图中,每条边在邻接表中对应了两个边表结点,如果在图的应用中需要对边进行标记,或删除边等,此时需要找到表示同一条边的两个边表结点,然后执行相同的操作,以保证数据的一致性,因此操作的实现比较麻烦。另一方面,如果在邻接表中,将所有的顶点按照顺序的方式存储,会使得顶点的删除操作所需的时间代价较大。首先在数组中删除一个元素,平均需要移动大约数组中一半的元素;其次,在删除一个顶点时,需要将与之相关联的所有边删除,如上所述,在无向图中删除一条边需要删除两个边表结点,较为复杂;再次,由于在删除某个顶点以后,会造成后续顶点在顶点数组中的位置发生变化,因此要判断所有边表结点的邻接点域是否需要修改,如果其邻接点域所指顶点位置发生变化,则需要使用新的指向替换原来的指向。以上操作总共需要Ο(|V|+|E|)的时间。解决这个问题的一种办法是,在删除顶点时,并不将数组中其后续顶点前移,只是将相应位置设置为空,然后删除与之关联的所有边。但是这种方法会使得在图中添加顶点之前需要先遍历顶点数组,查找数组中为空的位置,如果有则将新的顶点放入该位置,如果没有则放到数组的尾部。这样添加一个新顶点的操作实现会比较复杂。综合以上两点,在图的邻接表与逆邻接表的基础上,我们给出图的一种双链式存储结构以解决上述问题。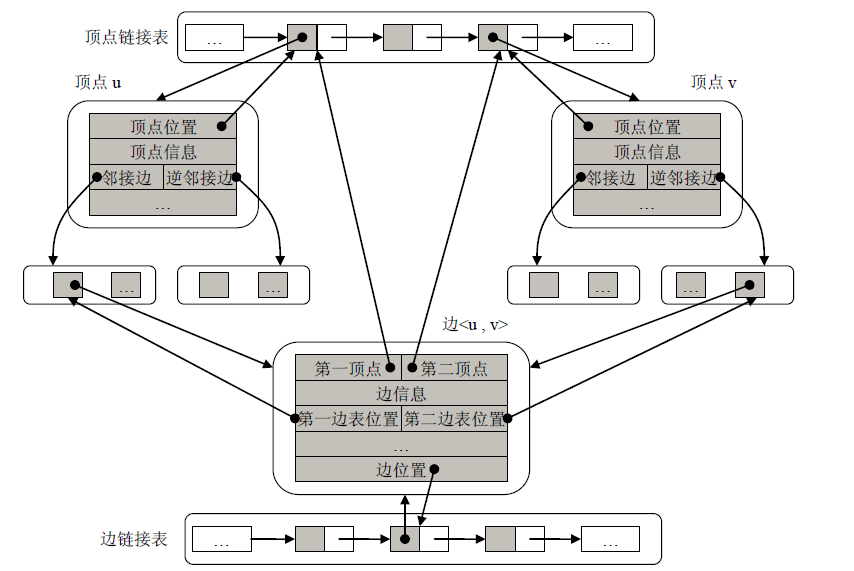
顶点中有3 个重要的指针域:顶点位置域、邻接边域、逆邻接边域。其中顶点位置域指向顶点在顶点链接表中所在的结点,以此可以在Ο(1)时间内确定顶点在图中的位置。在无向图中顶点的邻接边域指向的链接表存储了与该顶点关联的所有边的引用,顶点的逆邻接边域为空;而在有向图中,顶点的邻接边域指向的链接表存储了该顶点所有出边的引用,顶点的逆邻接边域指向的链接表存储了该顶点所有入边的引用。邻接边域和逆邻接边域相当于图中顶点的邻接表和逆邻接表。通过这两个域可以很快的找到与该顶点相连的所有顶点和边的信息。
边中有5个重要的指针域:第一顶点域、第二顶点域、第一边表位置域、第二边表位置域、边位置域。在有向图中,第一顶点域指向该边的起始顶点在顶点表中的位置,第二顶点域指向该边的终止顶点在顶点表中的位置;如果是无向图,则分别指向边的两个顶点在顶点表中的位置;通过这两个域可以在Ο(1)时间内定位与边关联的顶点。在有向图中,第一边表位置域指向边在其起始点的出边表中的位置,第二边表位置域指向边在其终止点的入边表中的位置;如果是无向图,则这两个域分别指向边在其第一、第二顶点的邻接边表(无向图的顶点只有邻接边表,无逆邻接边表)中的位置。边位置域指向边在边表中的位置,通过该域可以在Ο(1)时间内定位边在图中的位置。
双链式存储结构的顶点定义
public class Vertex {
private Object info; // 顶点信息
private LinkedList adjacentEdges; // 顶点的邻接边表
private LinkedList reAdjacentEdges; // 顶点的逆邻接边表,无向图时为空
private boolean visited; // 访问状态
private Node vexPosition; // 顶点在顶点表中的位置
private int graphType; // 顶点所在图的类型
private Object application; // 应用信息。例如求最短路径时为Path,求关键路径时为Vtime
// 构造方法:在图G中引入一个新顶点
public Vertex(Graph g, Object info) {
this.info = info;
adjacentEdges = new LinkedListDLNode();
reAdjacentEdges = new LinkedListDLNode();
visited = false;
graphType = g.getType();
vexPosition = g.insert(this);
application = null;
}
// 辅助方法:判断顶点所在图的类型
private boolean isUnDiGraphNode() {
return graphType == Graph.UndirectedGraph;
}
// 获取或设置顶点信息
public Object getInfo() {
return info;
}
public void setInfo(Object info) {
this.info = info;
}
// 与顶点的度相关的方法
public int getDeg() {
if (isUnDiGraphNode())
return adjacentEdges.getSize(); // 无向图顶点的(出/入)度即为邻接边表的规模
else
return getOutDeg() + getInDeg(); // 有向图顶点的度为出度与入度之和
}
public int getOutDeg() {
return adjacentEdges.getSize(); // 有(无)向图顶点的出度为邻接表规模
}
public int getInDeg() {
if (isUnDiGraphNode())
return adjacentEdges.getSize(); // 无向图顶点的入度就是它的度
else
return reAdjacentEdges.getSize();// 有向图顶点入度为逆邻接表的规模
}
// 获取与顶点关联的边
public LinkedList getAdjacentEdges() {
return adjacentEdges;
}
public LinkedList getReAdjacentEdges() {
if (isUnDiGraphNode())
return adjacentEdges; // 无向图顶点无逆邻接边表,其逆邻接边表就是邻接边表
else
return reAdjacentEdges;
}
// 取顶点在所属图顶点集中的位置
public Node getVexPosition() {
return vexPosition;
}
// 与顶点访问状态相关方法
public boolean isVisited() {
return visited;
}
public void setToVisited() {
visited = true;
}
public void setToUnvisited() {
visited = false;
}
// 取或设置顶点应用信息
protected Object getAppObj() {
return application;
}
protected void setAppObj(Object app) {
application = app;
}
// 重置顶点状态信息
public void resetStatus() {
visited = false;
application = null;
}
}
双链式存储结构的边定义
public class Edge {
public static final int NORMAL = 0;
public static final int MST = 1; // MST边
public static final int CRITICAL = 2;// 关键路径中的边
private int weight; // 权值
private Object info; // 边的信息
private Node edgePosition; // 边在边表中的位置
private Node firstVexPosition; // 边的第一顶点在顶点表中的位置
private Node secondVexPosition; // 边的第二顶点在顶点表中的位置
private Node edgeFirstPosition; // 边在第一(二)顶点的邻接(逆邻接)边表中的位置
private Node egdeSecondPosition;// 在无向图中就是在两个顶点的邻接表中的位置
private int type; // 边的类型
private int graphType; // 所在图的类型
// 构造方法:在图G中引入一条新边,其顶点为u、v
public Edge(Graph g, Vertex u, Vertex v, Object info) {
this(g, u, v, info, 1);
}
public Edge(Graph g, Vertex u, Vertex v, Object info, int weight) {
this.info = info;
this.weight = weight;
edgePosition = g.insert(this);
firstVexPosition = u.getVexPosition();
secondVexPosition = v.getVexPosition();
type = Edge.NORMAL;
graphType = g.getType();
if (graphType == Graph.UndirectedGraph) {
// 如果是无向图,边应当加入其两个顶点的邻接边表
edgeFirstPosition = u.getAdjacentEdges().insertLast(this);
egdeSecondPosition = v.getAdjacentEdges().insertLast(this);
} else {
// 如果是有向图,边加入起始点的邻接边表,终止点的逆邻接边表
edgeFirstPosition = u.getAdjacentEdges().insertLast(this);
egdeSecondPosition = v.getReAdjacentEdges().insertLast(this);
}
}
// get&set methods
public Object getInfo() {
return info;
}
public void setInfo(Object info) {
this.info = info;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public Vertex getFirstVex() {
return (Vertex) firstVexPosition.getData();
}
public Vertex getSecondVex() {
return (Vertex) secondVexPosition.getData();
}
public Node getFirstVexPosition() {
return firstVexPosition;
}
public Node getSecondVexPosition() {
return secondVexPosition;
}
public Node getEdgeFirstPosition() {
return edgeFirstPosition;
}
public Node getEdgeSecondPosition() {
return egdeSecondPosition;
}
public Node getEdgePosition() {
return edgePosition;
}
// 与边的类型相关的方法
public void setToMST() {
type = Edge.MST;
}
public void setToCritical() {
type = Edge.CRITICAL;
}
public void resetType() {
type = Edge.NORMAL;
}
public boolean isMSTEdge() {
return type == Edge.MST;
}
public boolean isCritical() {
return type == Edge.CRITICAL;
}
}
以下两种存储方式是第3种在有向图和无向图上面的具体化,并且节点用顺序存储结构。而双链式存储结构节点和边表都是链式存储结构。
2.4、十字链表---->适用于有向图
它是有向图的另一种链式结构。
思路:将邻接矩阵用链表存储,是邻接表、逆邻接表的结合。
1、每条弧对应一个结点(称为弧结点,设5个域)
2、每个顶点也对应一个结点(称为顶点结点,设3个域)
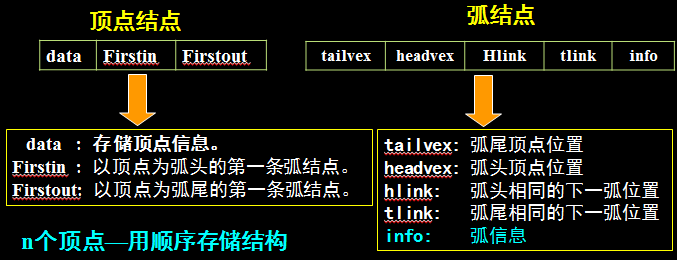
十字链表存储结构描述:
#define MAX_VERTEX_NUM 20
Typedef struct ArcBox { //弧结点结构
int tailvex , headvex ;
struct ArcBox * hlink , tlink;
InfoType *info;
} ArcBox;
Typedef struct VexNode{ //顶点结构
VertexType data;
ArcBox * firstin,*firstout;
} VexNode;
Typedef struct {
VexNode xlist[ MAX_VERTEX_NUM ]; //表头向量
int vexnum, arcnum;
} OLGraph; //图结构
例子:
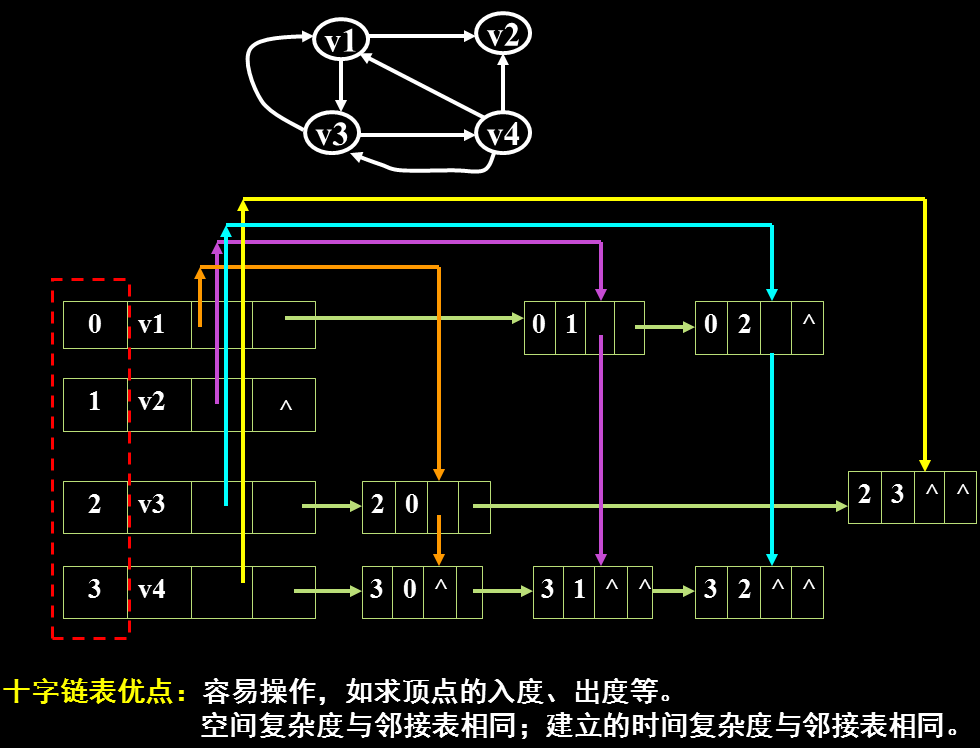
2.5、邻接多重表---->适用于无向图
这是无向图的另一种存储结构,当对边操作时,无向图应采用此种结构存储。
1、每条边只对应一个结点(称为边结点),设立6个域;
2、每个顶点也对应一个结点(顶点结点),设立2个域;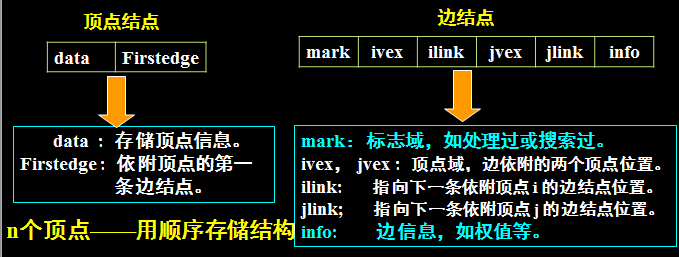
无向图的邻接多重表存储表示
typedef struct Ebox {
VisitIf mark; //访问标记
int ivex, jvex; //该边依附的两个顶点的位置
struct EBox *ilink, *jlink;
InfoType *info; //该边信息指针
} EBox;
typedef struct VexBox {
VertexType data;
EBox *firstedge; // 指向第一条依附该顶点的边
} VexBox;
typedef struct { // 邻接多重表
VexBox adjmulist[MAX_VERTEX_NUM];
int vexnum, edgenum;
} AMLGraph;
无向图邻接多重表-例子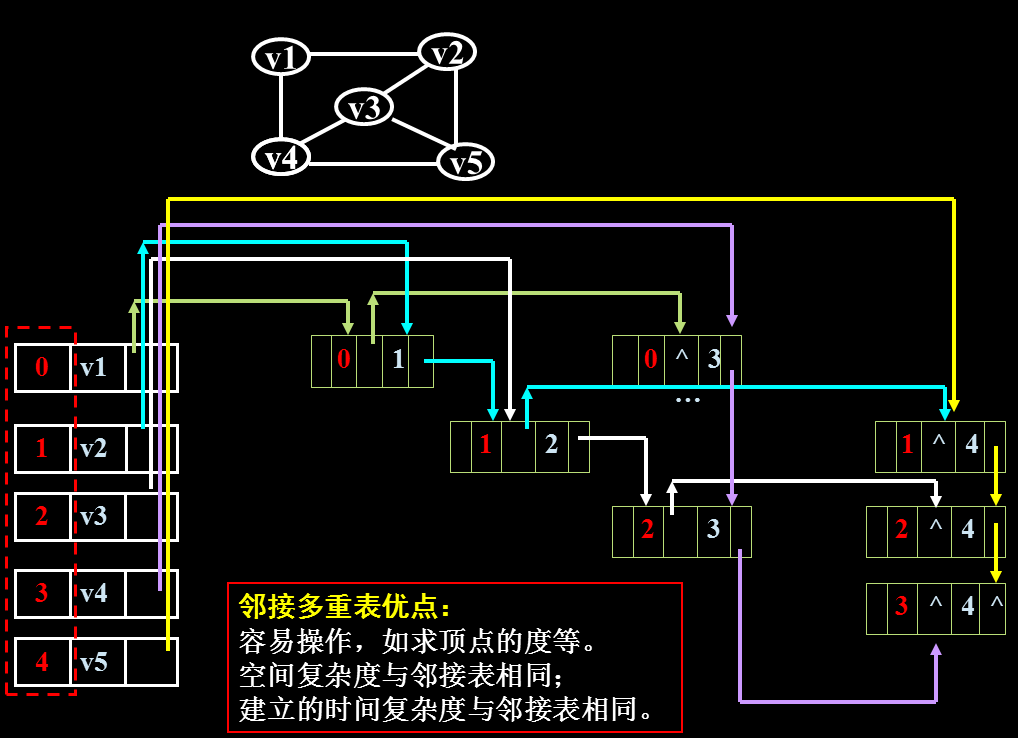




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律