数据结构---->图的应用(拓扑排序,关键路径)
七、图的应用
7.1、两种常用的活动网络( Activity Network):
① AOV网(Activity On Vertices)—用顶点表示活动的网络
AOV网定义:若用有向图表示一个工程,在图中用顶点表示活动,用弧表示活动间的优先关系。Vi 必须先于活动Vj 进行。则这样的有向图叫做用顶点表示活动的网络,简称AOV。
② AOE网(Activity On Edges)—用边表示活动的网络
AOE网定义:如果在无环的带权有向图中,用有向边表示一个工程中的活动,用边上权值表示活动持续时间,用顶点表示事件,则这样的有向图叫做用边表示活动的网络,简称AOE。
7.2、AOV网络的用途---拓扑排序
我们经常用有向图来描述一个工程或系统的进行过程。一般来说,一个工程可以分为若干个子工程,只要完成了这些子工程,就可以导致整个工程的完成。
AOV网络若用于教学计划的制定,可以解决:哪些课程是必须先修的,哪些课程是可以并行学习的。
拓扑排序
什么叫拓扑排序?
按照有向图给出的次序关系,将图中顶点排成一个线性序列,对于有向图中没有限定次序关系的顶点,则可以人为加上任意的次序关系。由此所得顶点的线性序列称之为拓扑有序序列
如何进行拓扑排序?
一、从有向图中选取一个没有前驱的顶点(即入度为零的顶点),并输出之;
二、从有向图中删去此顶点以及所有以它为尾的弧(即弧头顶点的入度减1);
重复上述两步,直到
全部顶点均已输出,拓扑有序序列形成,拓扑排序完成;
或图中还有未输出的顶点,但已跳出处理循环。这说明图中还剩下一些顶点,它们都有直接前驱,再也找不到没有前驱的顶点了。这时AOV网络中必定存在有向环。
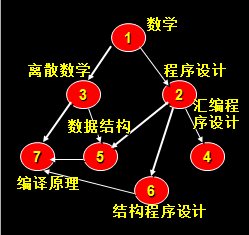
序号 1、2、3、4、5、6、7 前件的序号<后件的序号,合乎拓扑排序的要求
使用邻接矩阵实现拓扑排序:
算法的执行步骤:
1、找到全为零的第j 列,输出j
2、将第j 行的全部元素置为零
3、找到全为零的第k列,输出k
4、将第k行的全部元素置为零 …………………
反复执行3、4;直至所有元素输出完毕。
使用邻接表实现拓扑排序:
算法的执行步骤:
1、用一个数组记录每个结点的入度。将入度为零的结点进栈。
2、将栈中入度为零的结点V输出。
3、根据邻接表找到结点V的所有的邻接结点,并将这些邻接结点的入度减一。如果某一结点的入度变为零,则进栈。
4、反复执行 2、3;直至栈空为止。 …………………
次序执行结束,如果输出结点数等于图的结点总数,则有向图无环,否则有向图有环。
|
CountInDegree(G,indegree); //对各顶点求入度 InitStack(S); for ( i=0; i<G.vexnum; ++i) if (!indegree[i]) Push(S, i); //入度为零的顶点入栈 count=0; //对输出顶点计数 while (!EmptyStack(S)) { Pop(S, v); ++count; printf(v); for (w=FirstAdj(v); w; w=NextAdj(G,v,w)){ --indegree(w); // 弧头顶点的入度减一 if (!indegree[w]) Push(S, w); //新产生的入度为零的顶点入栈 } } if (count<G.vexnum)printf(“图中有回路”)
|
7.3AOE网络的用途:---确定关键路径
常用于大型工程的计划管理。利用AOE网络可以解决以下两个问题:
(1) 完成整个工程至少需要多少时间。(假设网络中没有环)?
(2) 为缩短完成工程所需的时间, 应当加快哪些活动? 或者说,哪些活动是影响工程进度的关键?
问题:假设以有向网表示一个施工流图,弧上的权值表示完成该项子工程所需时间。
问:哪些子工程项是“关键工程”?
即:哪些子工程项将影响整个工程的完成期限的。
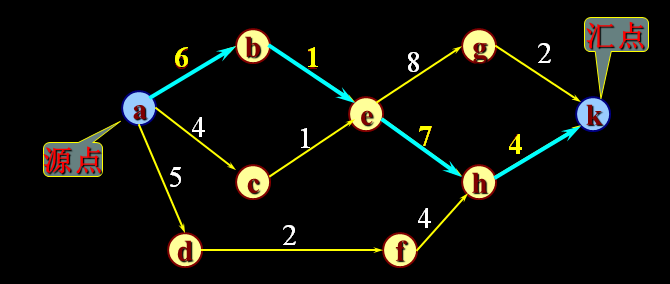
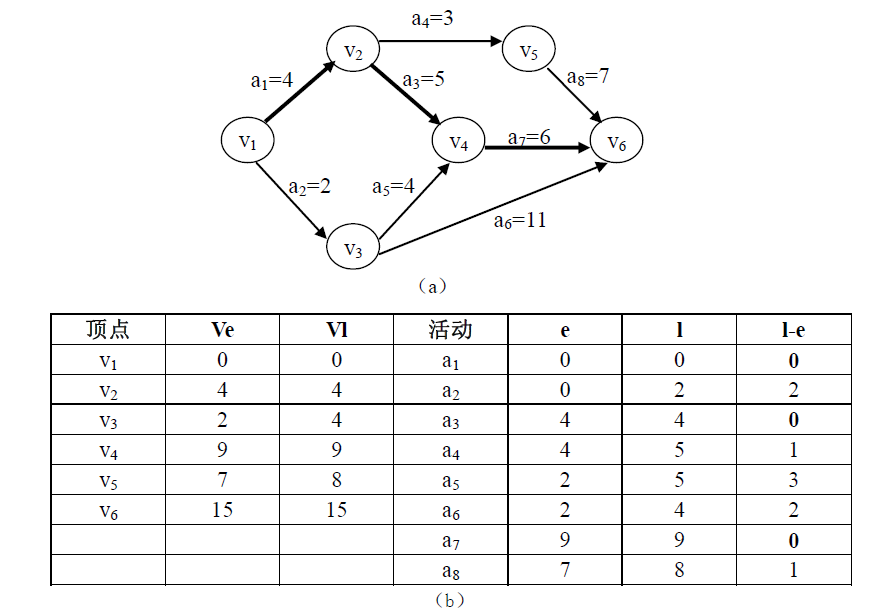
例设一个工程有11项活动,9个事件
事件V1——表示整个工程开始
事件V9——表示整个工程结束
(1) 完成整项工程至少需要多少时间?
(2) 哪些活动是影响工程进度的关键?
关键路径
- 在AOE网络中, 有些活动顺序进行,有些活动并行进行。
- 从源点到各个顶点,以至从源点到汇点的有向路径可能不止一条。这些路径的长度也可能不同。完成不同路径的活动所需的时间虽然不同,但只有各条路径上所有活动都完成了,整个工程才算完成。
- 完成整个工程所需的时间取决于从源点到汇点的最长路径长度,即在这条路径上所有活动的持续时间之和。这条路径长度最长的路径就叫做关键路径(Critical Path)。
整个工程完成的时间为:从有向图的源点到汇点的最长路径。
关键活动:该弧上的权值增加 将使有向图上的最长路径的长度增加。关键活动的最早开始时间 =关键活动的最迟开始时间
构造关键路径的方法:要用到拓扑排序和逆拓扑排序
事件发生时间的计算公式:
ve(源点) = 0; ve(k) = Max{ve(j) + dut(<j,k>)}
vl(汇点) = ve(汇点); vl(j) = Min{vl(k) – dut(<j, k>)}

开始vl=18
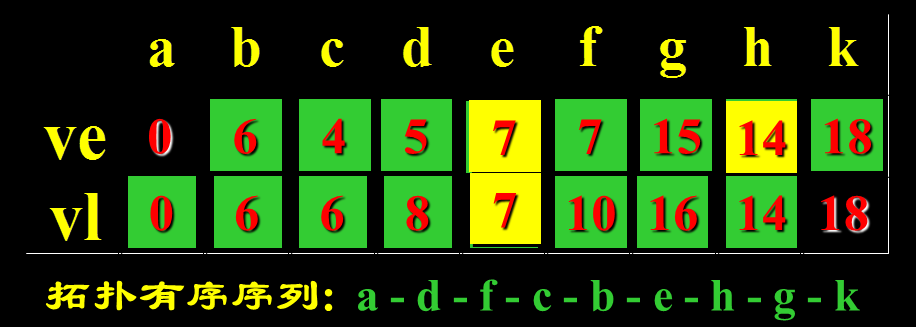
假设第i条弧为 <j,k>, 则 对第i项活动言
“活动(弧)”的最早开始时间 ee(i): ee(i) = ve(j);
“活动(弧)”的最迟开始时间 el(i): el(i) =vl(k)–dut(<j,k>);

算法描述
• 输入顶点和弧信息,建立其邻接表
• 计算每个顶点的入度
• 对其进行拓扑排序
排序过程中求顶点的Ve[i]
将得到的拓扑序列进栈
• 按逆拓扑序列求顶点的Vl[i]
• 计算每条弧的e[i]和l[i],找出e[i]=l[i]的关键活动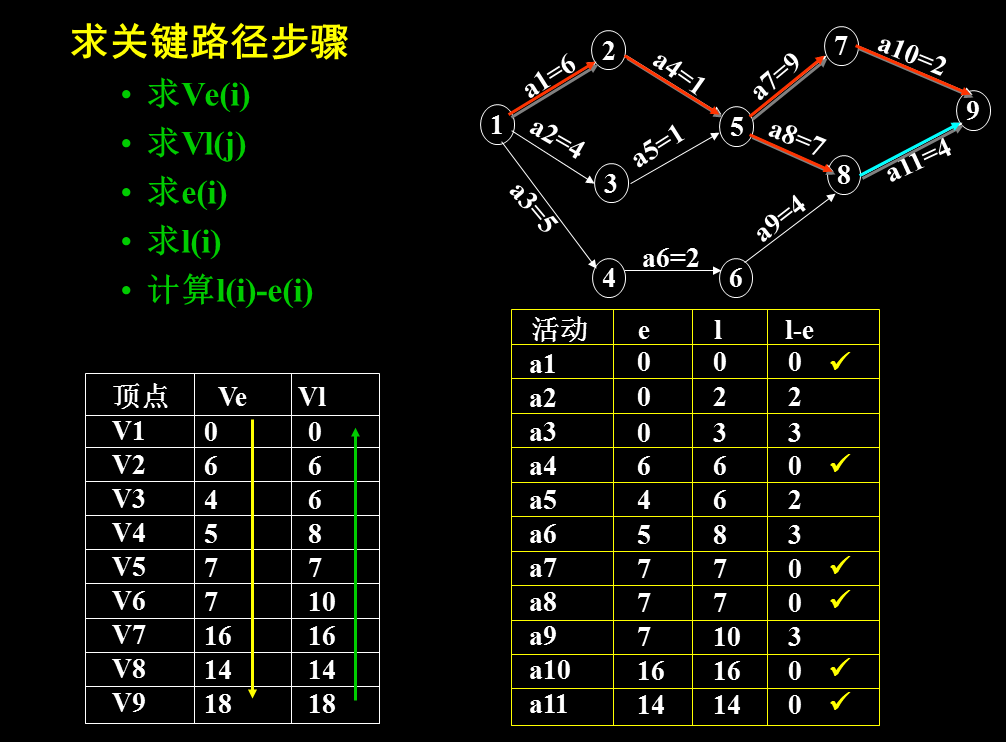




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律