数据结构---->树

   树

树结构中数据元素之间的逻辑关系是前驱唯一而后续不唯一，即数据元素之间是一对多的关系。如果直观的观察，树结构是具有分支的层次结构。树结构在客观世界中广泛存在，如行政区划、社会组织机构、家族世系等都可以抽象为树结构。

一、树的定义及基本术语

树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点，所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构。在这种层次结构中有一个结点具有特殊的地位，这个结点称为该树的根结点，或简称为树根。我们可以形 式地给出树的递归定义如下：

树（tree）是n（n≥0）个结点的有限集。它

1) 或者是一棵空树（n=0),空树中不包含任何结点。

2) 或者是一棵非空树（n>0),此时有且仅有一个特定的称为根（root）的结点;当n>1时，其余结点可分为m（m>0）个互不相交的有限集T1，T2，…，Tm， 其中每一个本身又是一棵树，并且称为根的子树（subtree）。

结点的层次和树的深度

结点的层次（level）从根开始定义，层次数为0的结点是根结点，其子树的根的层次数为1。若结点在L层，其子树的根就在L+1层。父子之间的连线是树的一条边。同一结点的孩子相互称为兄弟（sibling）。

树中结点的最大层次数称为树的深度（Depth）或高度。树中结点也有高度，其高度是以该结点为根的树的高度。

结点的度与树的度

结点拥有的子树的数目称为结点的度（Degree）。度为0的结点称为叶子（leaf）或终端结点。度不为0的结点称为非终端结点或分支结点。除根之外的分支结点也称为内部结点。

在树结构性质如下：

性质1   树中的结点数等于树的边数加1，也等于所有结点的度数之和加1。

性质1说明在树中结点总数与边的总数是相当的，基于这一事实，在对涉及树结构的算法复杂性进行分析时，可以用结点的数目作为规模的度量。

路径

在树中k+1 个结点通过k条边连接构成的序列{（v0,v1）,（v1,v2）, … ,（vk-1,vk）|k ≥ 0}，称为长度为k的路径（path）。

树中任意两个结点之间都存在唯一的路径。这意味着树既是连通的，同时又不会出现环路。从根结点开始，存在到其他任意结点的一条唯一路径，根到某个结点路径的长度，恰好是该结点的层次数。

祖先、子孙、堂兄弟

结点的祖先是从根到该 结点路径上的所有结点。以某结点为根的树中的任一结点都称为该结点的子孙。父亲在同一层次的结点互为堂兄弟。

有序树、m叉树、森林

如果将树中结点的各子树看成是从左至右是有次序的，则称该树为有序树；若不考虑子树的顺序则称为无序树。

树中所有结点最大度数为 m 的有序树称为m叉树。

森林（forest）是m（m≥0）棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。树和森林的概念相近。删去一棵树的根，就得到一个森林；反之，加上一个结点作树根，森林就变为一棵树。

树的抽象数据类型的定义。

ADT Tree{

数据对象 D：D  是具有相同性质的数据元素的集合。

数据关系 R：若 D=Φ则R =Φ；若 D≠Φ，则 R = {H}，H 是如下二元关系：

①在D中存在一个唯一的称为根的元素root,它在H下无前驱；

②除root以外,D中每个结点在H下都有且仅有一个前驱。

基本操作：

	getSzie  ()	返回树的结点数。
	getRoot()	返回树根结点。
	getParent(x)	返回结点x的父结点。
	getFirstChild(x)	返回结点x的第一个孩子。
	getNextSibling(x)	返回结点x的下一个兄弟结点，如果x是最后一个孩子，则返回空。
	getHeight(x)	返回以x为根的树的高度。
	insertChild(x,child)	将结点child为根的子树插入树中，作为结点x的子树。
	deleteChild(x,i)	删除结点x的第 i 棵子树。
	preOrder()inOrder()postOrder()levelOrder()	先序、后序、按层遍历x为根的树

 

}ADTTree

 

二、二叉树

最简单而极其重要的树结构——二叉树。因为任何树都可以转化为二叉树进行处理,并且二叉树适合计算机的存储和处理,因此二叉树是研究的重点。

2.1 二叉树的定义

每个结点的度均不超过2的有序树,称为二叉树(binaryTree)。与树的递归定义类似,二叉树的递归定义如下：二叉树或者是一棵空树,或者是一棵由一个根结点和两棵互不相交的分别称为根的左子树和右子树的子树所组成的非空树。

二叉树中每个结点的孩子数只能是0、1或2个，并且每个孩子都有左右之分。位于左边的孩子称为左孩子，位于右边的孩子称为右孩子；以左孩子为根的子树称为左子树，以右孩子为根的子树称为右子树。

2.2  二叉树的性质

性质2  在二叉树的第i层上最多有2^i个结点。

性质3  高度为h的二叉树至多有2^h+1-1 个结点。

性质4  对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1。

证明： 假设二叉树中结点总数为n，n1为度为 1 的结点。 于是有：n=n0+n1+n2

由性质1知：n =1×n1+2×n2+1(节点数=度数+1)

所以：n0 = n2 + 1

2.3两种特殊的二叉树

满二叉树：高度为k并且有 2^k+1-1 个结点的二叉树。在满二叉树中，每层结点都达到最大数，即每层结点都是满的，因此称为满二叉树。

完全二叉树：若在一棵满二叉树中，在最下层从最右侧起去掉相邻的若干叶子结点，得到的二叉树即为完全二叉树。

可以对满二叉树的结点进行编号，约定编号从根结点起，层间自上而下，层内自左而右，逐层由1到n进行标号。如果按照上述对满二叉树结点编号的方法，对具有n个结点的完全二叉树中结点进行编号，那么完全二叉树中1到n号结点的位置与满二叉树中1到n号结点的位置是一致的。可见,满二叉树必为完全二叉树,而完全二叉树不一定是满二叉树。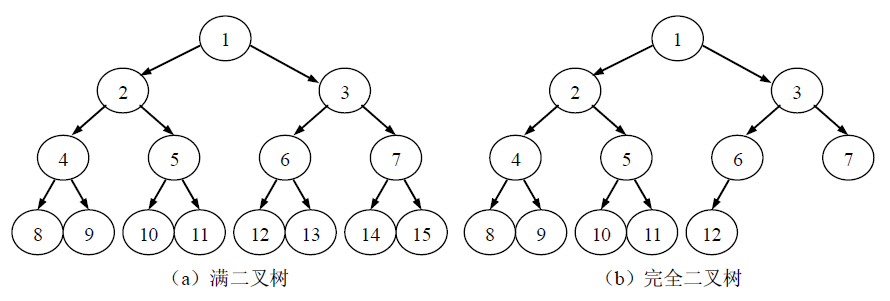

性质 5 有n 个结点的完全二叉树的高度为⎣log n⎦。

在固定结点数目的二叉树中，完全二叉树 的高度是最小的。

性质 6  含有n≥1个结点的二叉树的高度至多为n-1；高度至少为 ⎣log n⎦。

性质 7 如果对一棵有n个结点的完全二叉树的结点进行编号，则对任一结点 i(1≤i≤n)，有

⑴ 如果 i=1，则结点 i 是二叉树的根，无双亲；如果 i>1，则其双亲结点PARENT(i)是结点⎣i/2⎦。

⑵ 如果 2i>n，则结点 i 无左孩子；否则其左孩子是结点2i。

   如果 2i+1>n，则结点 i 无右孩子；否则其右孩子是结点 2i+1。

三、二叉树的存储结构

二叉树的存储结构有两种：顺序存储结构和链式存储结构。

3.1顺序存储结构

对于满二叉树和完全二叉树来说，可以将其数据元素逐层存放到一组连续的存储单元中,如图所示。用一维数组来实现顺序存储结构时，将二叉树中编号为 i 的结点存放到 数组中的第i个分量中。如此根据性质7，可以得到结点i的父结点、左右孩子结点分别 存放在 ⎣i/2⎦、2i 以及 2i+1 分量中。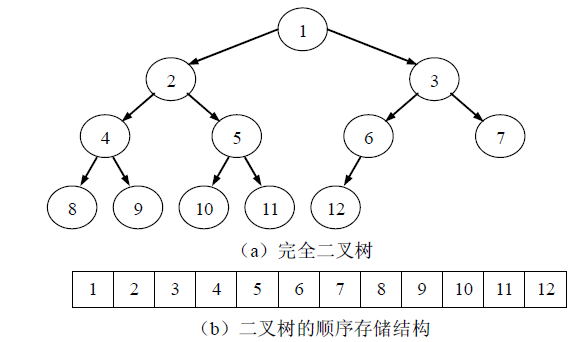

这种存储方式对于满二叉树和完全二叉树是非常合适也是高效方便的。因为满二叉树和完全二叉树采用顺序存储结构既不浪费空间，也可以根据公式很快的确定结点之间的关系。 但是对于一般的二叉树而言，必须用“虚结点”将一棵二叉树补成一棵完全二叉树来存储，否则无法确定结点之间的前驱后续关系，但是这样一来就会造成空间的浪费。一种极端的情 况是,为了存储k个结点，需要2^k-1个存储单元，此时存储空间浪费巨大，这是顺序存储结构的一个缺点。

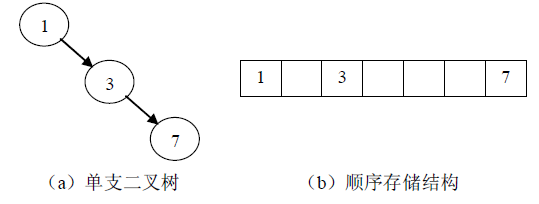
3.2链式存储结构

设计不同的结点结构可构成不同的链式存储结构。在二叉树中每个结点都有两个孩子，则可以设计每个结点至少包括3个域：数据域、左孩子域和右孩子域。数据域存放数据元素，左孩子域存放指向左孩子结点的指针，右孩子域存放指向右孩子结点的指针。利用此结点结构得到的二叉树存储结构称为二叉链表。容易证明在具有n个结点的二叉链表中有n+1个空链域。

为了方便找到父结点，可以在上述结点结构中增加一个指针域，指向结点的父结点。采用此结点结构得到的二叉树存储结构称为三叉链表。在具有n个结点的三叉链表中也有n+1个空链域。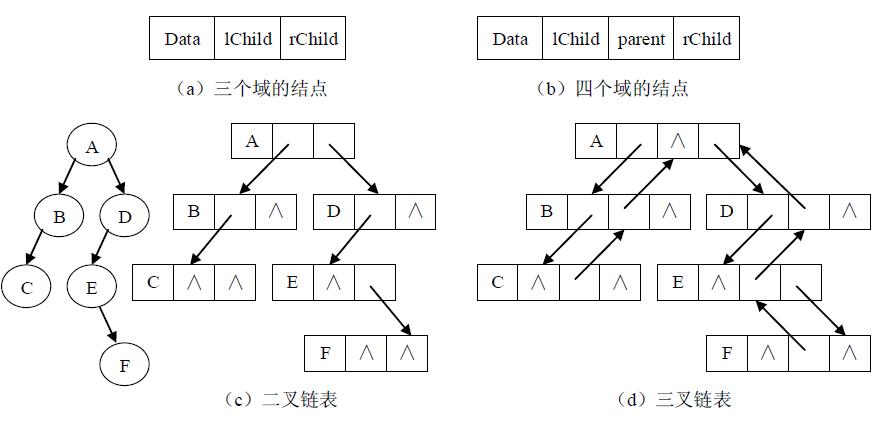

为了方便的找到父结点，我们以三叉链表作为二叉树的存储结构。

代码：二叉树存储结构结点定义

package tree;

import tree.Node;

public class BinTreeNode implements Node {

	private Object data; // 数据域
	private BinTreeNode parent; // 父结点
	private BinTreeNode lChild; // 左孩子
	private BinTreeNode rChild; // 右孩子
	private int height; // 以该结点为根的子树的高度
	private int size; // 该结点子孙数（包括结点本身）

	public BinTreeNode() {
		this(null);
	}

	public BinTreeNode(Object e) {
		data = e;
		parent = lChild = rChild = null;
		height = 0;
		size = 1;
	}

	/****** Node接口方法 ******/
	public Object getData() {
		return data;
	}

	public void setData(Object obj) {
		data = obj;
	}

	/****** 辅助方法,判断当前结点位置情况 ******/
	// 判断是否有父亲
	public boolean hasParent() {
		return parent != null;
	}

	// 判断是否有左孩子
	public boolean hasLChild() {
		return lChild != null;
	}

	// 判断是否有右孩子
	public boolean hasRChild() {
		return rChild != null;
	}

	// 判断是否为叶子结点
	public boolean isLeaf() {
		return !hasLChild() && !hasRChild();
	}

	// 判断是否为某结点的左孩子
	public boolean isLChild() {
		return (hasParent() && this == parent.lChild);
	}

	// 判断是否为某结点的右孩子
	public boolean isRChild() {
		return (hasParent() && this == parent.rChild);
	}

	/****** 与height相关的方法 ******/
	// 取结点的高度,即以该结点为根的树的高度
	public int getHeight() {
		return height;
	}

	// 更新当前结点及其祖先的高度
	public void updateHeight() {
		int newH = 0;// 新高度初始化为0,高度等于左右子树高度加1中大的
		if (hasLChild())
			newH = Math.max(newH, 1 + getLChild().getHeight());
		if (hasRChild())
			newH = Math.max(newH, 1 + getRChild().getHeight());
		if (newH == height)
			return; // 高度没有发生变化则直接返回
		height = newH; // 否则更新高度
		if (hasParent())
			getParent().updateHeight(); // 递归更新祖先的高度
	}

	/****** 与size相关的方法 ******/
	// 取以该结点为根的树的结点数
	public int getSize() {
		return size;
	}

	// 更新当前结点及其祖先的子孙数
	public void updateSize() {
		size = 1; // 初始化为1,结点本身
		if (hasLChild())
			size += getLChild().getSize(); // 加上左子树规模
		if (hasRChild())
			size += getRChild().getSize(); // 加上右子树规模
		if (hasParent())
			getParent().updateSize(); // 递归更新祖先的规模
	}

	/****** 与parent相关的方法 ******/
	// 取父结点
	public BinTreeNode getParent() {
		return parent;
	}

	// 断开与父亲的关系
	public void sever() {
		if (!hasParent())
			return;
		if (isLChild())
			parent.lChild = null;
		else
			parent.rChild = null;
		parent.updateHeight(); // 更新父结点及其祖先高度
		parent.updateSize(); // 更新父结点及其祖先规模
		parent = null;
	}

	/****** 与lChild相关的方法 ******/
	// 取左孩子
	public BinTreeNode getLChild() {
		return lChild;
	}

	// 设置当前结点的左孩子,返回原左孩子
	public BinTreeNode setLChild(BinTreeNode lc) {
		BinTreeNode oldLC = this.lChild;
		if (hasLChild()) {
			lChild.sever();
		} // 断开当前左孩子与结点的关系
		if (lc != null) {
			lc.sever(); // 断开lc与其父结点的关系
			this.lChild = lc; // 确定父子关系
			lc.parent = this;
			this.updateHeight(); // 更新当前结点及其祖先高度
			this.updateSize(); // 更新当前结点及其祖先规模
		}
		return oldLC; // 返回原左孩子
	}

	/****** 与rChild相关的方法 ******/
	// 取右孩子
	public BinTreeNode getRChild() {
		return rChild;
	}

	// 设置当前结点的右孩子,返回原右孩子
	public BinTreeNode setRChild(BinTreeNode rc) {
		BinTreeNode oldRC = this.rChild;
		if (hasRChild()) {
			rChild.sever();
		} // 断开当前右孩子与结点的关系
		if (rc != null) {
			rc.sever(); // 断开lc与其父结点的关系
			this.rChild = rc; // 确定父子关系
			rc.parent = this;
			this.updateHeight(); // 更新当前结点及其祖先高度
			this.updateSize(); // 更新当前结点及其祖先规模
		}
		return oldRC; // 返回原右孩子
	}
}

以updateHeight ()为例，讨论时间复杂度。

updateHeight ()：若当前结点v的孩子发生变化，就需要使用updateHeight()方法更新当前结点及其祖先结点的高度。因为在二叉树中任何一个结点的高度，都等于其左右子树的高度中大者加1，而左右子树的高度只需要获取该结点左右孩子的高度即可获得，只需要Θ(1)时间。续而从v出发沿parent引用逆行向上，依次更新各祖先结点的高度即可。如果在上述过程中，发现某个结点的高度没有发生变化，算法可以直接终止。综上所述，当对一个结点v调用 updateHeight()方法时，若v的层数为level(v)，则最多只需要更新level(v)+1个结点的高度，因此算法的时间复杂度T(n)=Ο(level(v))。

四、二叉树遍历及其实现

4.1、遍历

所谓树的遍历,就是按照某种次序访问树中的所有结点，且每个结点恰好访问一次。也就是说，按照被访问的次序，可以得到由树中所有结点排成的一个序列。树的遍历也可以看成是人为的将非线性结构线性化。这里的"访问"是广义的，可以是对结点作各种处理，例如输出结点信息、更新结点信息等。

对左子树、根节点、右子树的访问顺序不同，可知可知共有A(3,3)=6种遍历方案，如果规定对左子树的遍历先于对右子树的遍历，那么还剩下3种情况：DLR、LDR、LRD。根据对根访问的不同顺序，分别称DLR为先根（序）遍历，LDR为中根（序）遍历，LRD 为后根（序）遍历。

⑴  先序遍历（DLR）二叉树的操作定义为： 若二叉树为空，则空操作；否则

①  访问根结点；

②  先序遍历左子树；

③  先序遍历右子树。

⑵  中序遍历（LDR）二叉树的操作定义为： 若二叉树为空，则空操作；否则

①  中序遍历左子树；

②  访问根结点；

③  中序遍历右子树。

⑶  后序遍历（LRD）二叉树的操作定义为： 若二叉树为空，则空操作；否则

①  后序遍历左子树；

②  后序遍历右子树；

③  访问根结点。

下面先以一棵二叉树表示一个算术表达式，然后对其进行遍历。以二叉树表示表达式的递归定义如下：若表达式为数或简单变量，则相应二叉树中仅有一个根结点；若表达式=（第一操作数）（运算符）（第二操作数），则相应二叉树用左子树表示第一操作数，用右子树表示第二操作数，根结点存放运算符。下述表达式对应的二叉树如下

a＋(b－c)×d－e／f

 

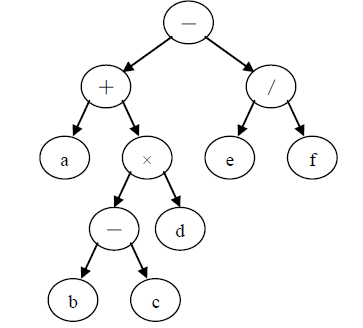
如果对该二叉树进行三种遍历，分别得到的遍历序列如下

先序遍历：－＋a×－bcd/ef

中序遍历：a＋b－c×d－e/f

后序遍历：abc－d×＋ef/－

从表达式上看，以上三个序列正好是表达式的前缀表示（波兰式）、中缀表示和后缀表示（逆波兰式）。在计算机中，使用后缀表达式易于求值。

4.2、DLR、LDR、LRD的递归实现

算法 preOrder

//先序遍历二叉树
	public Iterator preOrder() {
		LinkedList list = new LinkedListDLNode();
		preOrderRecursion(this.root,list);
		return list.elements();
	}
	//先序遍历的递归算法
	private void preOrderRecursion(BinTreeNode rt, LinkedList list){
		if (rt==null) return;					//递归基,空树直接返回
		list.insertLast(rt);					//访问根结点
		preOrderRecursion(rt.getLChild(),list);	//遍历左子树
		preOrderRecursion(rt.getRChild(),list);	//遍历右子树
	}

算法中是将结点加入链接表list的尾部作为对结点的访问，在算法的递归执行过程中，每个结点访问且仅被访问一次，因此算法的时间复杂度T(n) =Ο(n)。

4.3、DLR、LDR、LRD的非递归实现

二叉树的先序、中序和后序遍历操作，其不同之处仅在于访问访问根、左子树、右子树的顺序不同而已，实则三种遍历方法的递归执行过程是一样的。下图中用带箭头的虚线表示了三种遍历算法的递归过程。其中，向下的箭头表示更深一层的递归调用，向上的箭头表示从递归调用推出返回。在图中可以看到每个结点在遍历过程中都被途经3次，三种不同的遍历只是在该执行过程中的不同时机返回根结点而已。先序遍历是在第一次向下进入根结点时访问根结点，中序遍历是第二次从左子树递归调用返回时访问根，后序遍历是第三次从右子树递归调用返回时访问根。虚线旁边的①、②、③就是三种不同的访问根 结点的时机，分别对应先序、中序和后序遍历。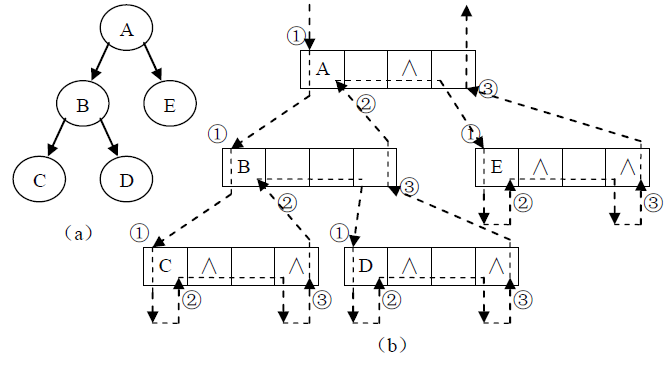

根据上述先序、中序和后序遍历递归算法的执行过程，可以写出相应的先序、中序和后序遍历的非递归算法。

算法 2  preOrder(也是将结点加入链接表 list 的尾部作为对结点的访问，使用参照上面)

//先序遍历的非递归算法
	private void preOrderTraverse(BinTreeNode rt, LinkedList list){
		if (rt==null) return;
		BinTreeNode p = rt;
		Stack s = new StackSLinked();
		while (p!=null){
			while (p!=null){								//向左走到尽头
				list.insertLast(p);							//访问根
				if (p.hasRChild()) s.push(p.getRChild());	//右子树根结点入栈
				p = p.getLChild();							
			}
			if (!s.isEmpty()) p = (BinTreeNode)s.pop();		//右子树根退栈遍历右子树
		}
	}

算法说明：preOrderTraverse 方法以一棵树的根结点 rt以及链接表list作为参数。如果rt为空直接返回，否则p指向rt，并先序遍历以p为根的树。在preOrderTraverse内层循环中，沿着根结点p一直向左走，沿途访问经过的根结点，并将这些根结点的非空右子树入栈，直到p为空。此时应当取出沿途最后碰到的非空右子树的根，即栈顶结点（以p指向），然后在外层循环中继续先序遍历这棵以 p 指向的子树。如果堆栈为空，则表示再没有的右子 树需要遍历，此时结束外层循环，完成整棵树的先序遍历。如果以 rt 为根的树的结点数为 n，由于每个结 点访问且仅被访问一次 ，并且每个结点最多入栈一次和出栈一次，因此preOrderTraverse 的时间复杂度 T(n)=Ο(n)。

算法3  inOrder

//中序遍历的非递归算法
	private void inOrderTraverse(BinTreeNode rt, LinkedList list){
		if (rt==null) return;
		BinTreeNode p = rt;
		Stack s = new StackSLinked();
		while (p!=null||!s.isEmpty()){
			while (p!=null){		//一直向左走
				s.push(p);			//将根结点入栈
				p = p.getLChild();
			}
			if (!s.isEmpty()){
				p = (BinTreeNode)s.pop();//取出栈顶根结点访问之
				list.insertLast(p);
				p = p.getRChild();		//转向根的右子树进行遍历
			}//if 
		}//out while
	}
	

算法说明：inOrderTraverse 方法以一棵树的根结点rt 以及链接表 list 作为参数。如果 rt 为空直接返回，否则 p 指向rt，并中序遍历以 p 为根的树。在 inOrderTraverse内层循环 中，沿着根结点 p 一直向左走，沿途将根结点入栈，直到 p 为空。此时应当取出上一层根结 点访问之，然后转向该根结点的右子树进行中序遍历。如果堆栈和 p 都为空，则说明没有更多的子树需要遍历，此时结束外层循环，完成整棵树的遍历。inOrderTraverse的时间复杂度与preOrderTraverse一样T(n)=Ο(n)。

算法4  postOrder

//后序遍历的非递归算法
	private void postOrderTraverse(BinTreeNode rt, LinkedList list){
		if (rt==null) return;
		BinTreeNode p = rt;
		Stack s = new StackSLinked();
		while(p!=null||!s.isEmpty()){
			while (p!=null){		//先左后右不断深入
				s.push(p);			//将根节点入栈
				if (p.hasLChild()) p = p.getLChild();
				else p = p.getRChild();
			}
			if (!s.isEmpty()){
				p = (BinTreeNode)s.pop();		//取出栈顶根结点访问之
				list.insertLast(p);
			}
			//满足条件时，说明栈顶根节点右子树已访问，应出栈访问之
			while (!s.isEmpty()&&((BinTreeNode)s.peek()).getRChild()==p){
				p = (BinTreeNode)s.pop();
				list.insertLast(p);
			}
			//转向栈顶根结点的右子树继续后序遍历
			if (!s.isEmpty()) p = ((BinTreeNode)s.peek()).getRChild();
			else p = null;
		}
	}

算法说明：postOrderTraverse方法以一棵树的根结点 rt 以及链接表 list 作为参数。 如果 rt 为空直接返回，否则p 指向 rt，并后序遍历以 p 为根的树。在 postOrderTraverse 内层 第一个 while 循环中，沿着根结点 p 先向左子树深入，如果左子树为空，则向右子树深入， 沿途将根结点入栈，直到 p 为空。第一个 if 语句说明应当取出栈顶根结点访问，此时栈顶 结点为叶子或无右子树的单分支结点。访问p 之后，说明以 p 为根的子树访问完毕，判断 p 是否为其父结点的右孩子（当前栈顶即为其父结点），如果是，则说明只要访问其父亲就可 以完成对以 p 的父亲为根的子树的遍历，以内层第二个 while 循环完成；如果不是，则转向其父结点的右子树继续后序遍历。如果堆栈和 p 都为空，则说明没有更多的子树需要遍历， 此时结束外层循环，完成整棵树的遍历。postOrderTraverse的时间复杂度分析和先序、中序 遍历算法一样，其时间复杂度 T(n) = Ο(n)。

4.4、层次遍历

层次遍历可以通过一个队列来实现，

算法5  levelOrder

//按层遍历二叉树
	public Iterator levelOrder(){
		LinkedList list = new LinkedListDLNode();
		levelOrderTraverse(this.root,list);
		return list.elements();
	}
	//使用对列完成二叉树的按层遍历
	private void levelOrderTraverse(BinTreeNode rt, LinkedList list){
		if (rt==null) return;
		Queue q = new QueueArray();
		q.enqueue(rt);			//根结点入队
		while (!q.isEmpty()){
			BinTreeNode p = (BinTreeNode)q.dequeue();	//取出队首结点p并访问
			list.insertLast(p);
			if (p.hasLChild()) q.enqueue(p.getLChild());//将p的非空左右孩子依次入队
			if (p.hasRChild()) q.enqueue(p.getRChild());
		}
	}

算法中，每个节点依次入队一次、出队一次并访问一次，因此算法的时间复杂度T(n) =Ο(n)，n 为以 rt 为根的树的结点数。

下面来分析二叉树其他基本操作的实现。由于在 BinTreeNode中结点的高度、规模等信息已经保存，并且在发生变化时都进行了更新，因此 getSzie()、getHeight()操作在常数时间内就能完成。isEmpty ()、getRoot()在根结点引用的基础上进行简单的比较和返回即可。

4.5、find(e)方法的实现。

算法6  find

//在树中查找元素 e，返回其所在结点

public BinTreeNode find(Object e) {

returnsearchE(root,e);

}

//递归查找元素 e

private BinTreeNodesearchE(BinTreeNodert, Object e) {

 

if(rt==null) return null;

if (strategy.equal(rt.getData(),e))return rt;      //如果是根结点，返回根

BinTreeNode v = searchE(rt.getLChild(),e); //否则在左子树中找

if (v==null) v = searchE(rt.getRChild(),e);     //没找到，在右子树中找

return v;

}

五、树、森林

5.1  树的存储结构

树的存储结构主要有以下三种。

5.1.1双亲表示法

设T 是一棵树，表示 T 的一种最简单的方法是用一个一维数组存储每个结点，数组的下标就是结点的位置指针，每个结点中有一个指向各自的父亲结点的数组下标的域。由于树中每个结点的父亲是唯一的，所以上述的父亲数组表示法可以唯一地表示任何一棵树。下图说明了这种存储结构。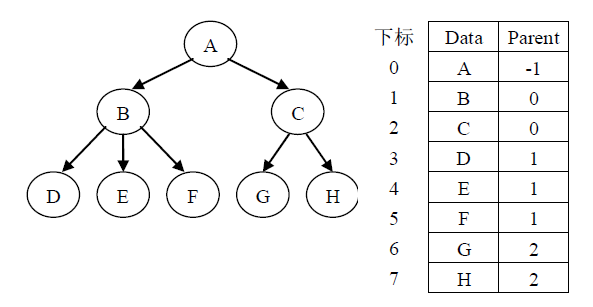

 

在这种表示法下，寻找一个结点的父结点只需要O(1)时间。在树中可以从一个结点出发找出一条向上延伸到达其祖先的路径，即从一个结点到其父亲，再到其祖父等等。求这样的路径所需的时间正比于路径上结点的个数。在树的父亲数组表示法中，对于涉及查询儿子和兄弟信息的树操作，可能要遍历整个数组。为了节省查询时间，可以规定指示儿子的数组下标值大于父亲的数组下标值，而指示兄弟结点的数组下标值随着兄弟的从左到右是递增的，

5.1.2孩子链表表示法

树的另一种常用的表示方法就是孩子链表表示法.这种表示法用一个线性表来存储树的所有结点信息，称为结点表。对每个结点建立一个孩子表。孩子表中只存储孩子结点的地址信息，可以是指针，数组下标甚至内存地址。由于每个结点的孩子数目不定，因此孩子表常用单链表来实现，因此这种表示法称为孩子链表表示法。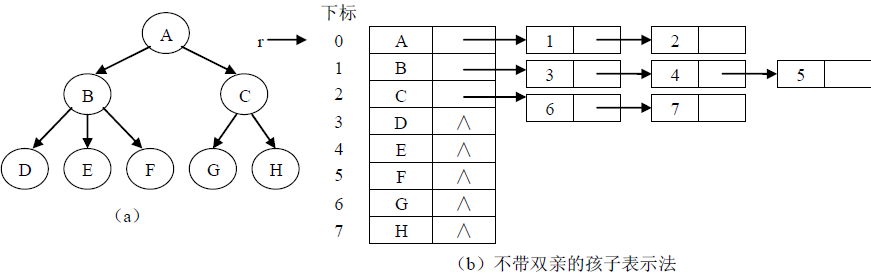

在孩子链表表示法中，通过某个结点找到其孩子较为容易，只需要遍历其孩子链表即可找到其所有孩子结点，然而要找到某个结点的父结点却需要对每个结点的孩子链表进行遍 历，比较麻烦。因此可以在孩子链表表示法的基础上结合双亲表示法，在每个结点中再附设一个指示双亲结点的域，这样就可以在 O(1)时间内找到父结点。如下图所示。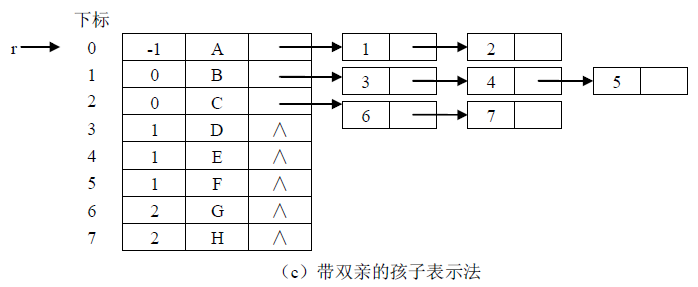

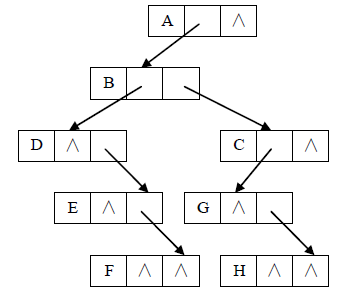
5.1.3孩子兄弟表示法

树的孩子兄弟表示法又称为二叉树表示法。每个结点除了data 域外，还含有两个域，分别指向该结点的第一个孩子和右邻兄弟。（树和上图的相同）

5.2  树、森林与二叉树的相互转换

通过树的孩子兄弟表示法可以看到，树和二叉树都可以使用二叉链表作为存储结构。则以二叉链表可以导出树与二叉树之间的一个对应关系。也就是说给出一棵树可以将其唯一地对应到一棵二叉树，从实际的存储结构来看，它们的二叉链表是相同的，只是解释不同而已。下图展示了一个树与二叉树对应关系的例子。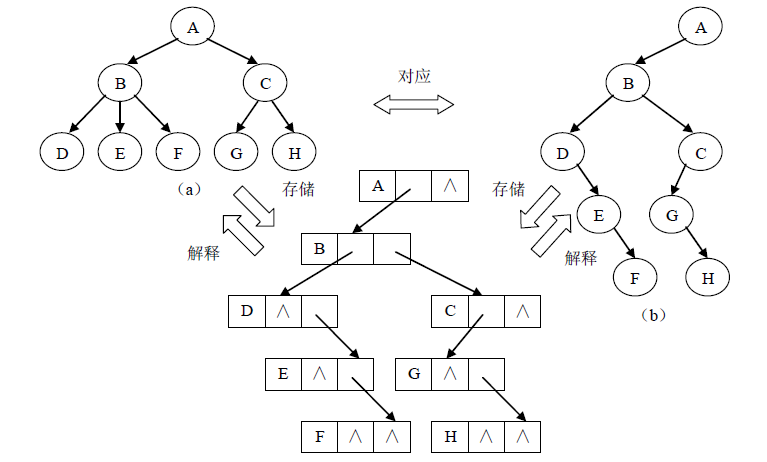

从树的孩子兄弟表示法的定义知道，任何一棵和某个树相对应的二叉树，其右子树必为空。下面我们给出将一棵树转换为二叉树的方法：将树中每个结点的第一个孩子转化为二叉树中对应结点的左孩子，将该结点右边的第一个兄弟转化为二叉树中该结点的右孩子。这实际上就是树的孩子兄弟表示法。

森林是若干棵树的集合。树可以转换为二叉树，森林同样也可以转换为二叉树。因此，森林也可以方便的使用孩子兄弟链表表示。森林转换为二叉树的方法是：

① 将森林中的每一棵树转换为相应的二叉树。

② 将所得的第一棵二叉树不动，从第二棵二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树根结点的右孩子。

由以上两个步骤得到的二叉树就是森林转换得到的二叉树。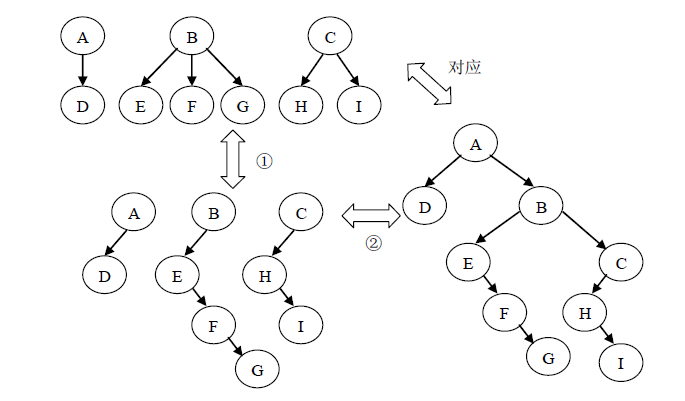

森林和树都可以转换为二叉树，二者的不同是：树转换为二叉树，其根结点的右子树必然为空；而森林转换为二叉树后，其根结点有右孩子（不考虑森林退化为树和森林与树为空的情况）

 

将一棵二叉树还原为树或森林，具体方法如下：按层次序列对二叉树中每个结点做如下操作①  如果是根结点或者是左孩子结点，那么不做任何改动；②如果是右孩子将其父结点设置为其当前父亲的父亲，若其当前父亲的父亲为空，则改动后其父亲为空。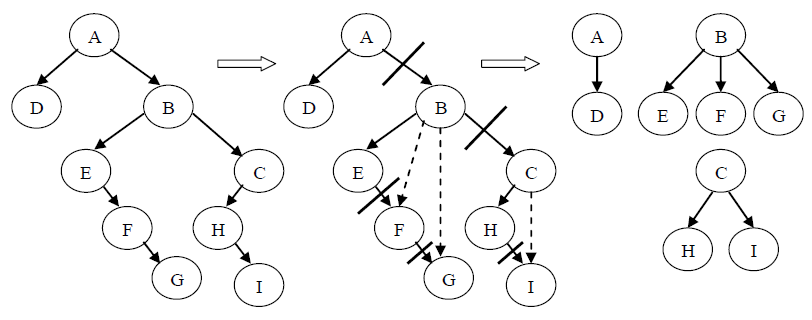

这种对应关系导致森林或树与二叉树之间可以相互转换，这种相互转换可以进行递归的形式定义。

1.森林转换成二叉树

如果F={T1, T2, … , Tm}是森林（m=1 时为树），则可以按照如下规则转换成一棵二叉树

B=（root, LB, RB）。

①   若 F 为空，则 B 为空树。

②   若F非空，则B的根root即为森林中第一棵树的根ROOT(T1)；B的左子树LB是从T1中根结点的子树森林F1  转换而成的二叉树；其右子树RB是森林中除第一棵树T1之外的森林F'={T2, T3,… , Tm}转换而成的二叉树。

2.二叉树转换成森林

如果B=（root, LB, RB）是一棵二叉树，则可以按照如下规则转换成森林F={T1, T2, … , Tm}。

①若 B 为空，则F 为空。

②若B非空，则F中第一棵树的根ROOT(T1)  即为二叉树B的根root；T1中根结点的子树森林F1 是由B的左子树LB是转换而成的森林；F中除第一棵树T1之外的森林F'={T2, T3, … , Tm}是由B的右子树RB是转换而成的森林。通过上述递归定义容易写出森林与二叉树相互转换的递归算法。同时森林和树的操作可以转换成二叉树的操作来实现。

5.3  树与森林的遍历

5.3.1树的遍历

由树的定义可以得到两种次序遍历树的方法：

⑴  先根遍历 若树非空，则遍历方法为：

①  访问树的根结点，

②  从左到右，依次先根遍历根的每棵子树。

⑵  后根遍历 若树非空，则遍历方法为：

①  从左到右，依次后根遍历根的每棵子树，

②  访问树的根结点。

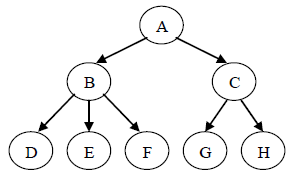
   图中树的先根遍历序列为：ABDEFCGH

   图中树的后根遍历序列为：DEFBGHCA

5.3.2森林的遍历

森林的遍历可以有以下三种方法：

⑴  先序遍历 若森林非空，则：

①  访问森林中第一棵树的根结点；

②  先序遍历第一棵树中根结点的子树森林；

③  先序遍历除去第一棵树后剩余的树构成的森林。

⑵  中序遍历 若森林非空，则：

①  中序遍历第一棵树中根结点的子树森林；

②  访问森林中第一棵树的根结点；

③  中序遍历除去第一棵树后剩余的树构成的森林。

⑶  后序遍历 若森林非空，则：

① 后序遍历第一棵树中根结点的子树森林；

② 后序遍历除去第一棵树后剩余的树构成的森林；

③ 访问森林中第一棵树的根结点。

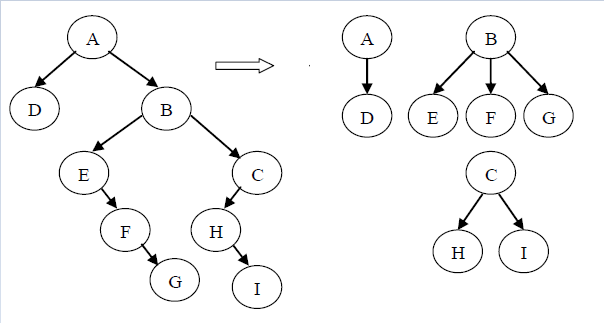
图中森林的先序遍历序列为：ADBEFGCHI

图中森林的中序遍历序列为：DAEFGBHIC

图中森林的后序遍历序列为：DGFEIHCBA

对照二叉树与森林之间的转换方法可以发现，森林的先序、中序、后序遍历与其相对应的二叉树的先序、中序、后序遍历的结果是相同的，因此可以用相应二叉树的遍历来验证森林的遍历结果。另外树可以看成只有一棵树的森林，所以树的先根遍历和后根遍历可以分别与森林的先序遍历和中序遍历对应，因此也就可以对应为相应二叉树的先序和中序遍历。由此可见，以二叉链表作为存储结构时，树的先根遍历和后根遍历可以借助相应二叉树的先序遍历和中序遍历的算法实现。

5.3.3  由遍历序列还原树结构

由于森林（包括树）的各种遍历可以对应为相应二叉树的遍历，如果通过遍历序列能还原为二叉树，也就可以相应的还原为森林。因此我们只分析二叉树的遍历序列还原为二叉树的问题。

首先通过二叉树的一种遍历序列是无法还原二叉树的。如果在二叉树的三种遍历序列中给出其中的两种，是否可以唯一确定一棵二叉树呢？

由先序和中序遍历序列还原二叉树：由二叉树的先序与中序序列可以唯一确定一棵二叉树。因为，二叉树的先序遍历先访问根结点D，其次遍历左子树 L，然后遍历右子树 R。即 在先序遍历序列中，第一个结点必为根结点；而在中序遍历时，先遍历左子树 L，然后访问根结点 D，最后遍历右子树R，因此中序遍历序列被根结点分为两部分：根结点之前的部分 为左子树结点中序序列，根结点之后的为右子树结点中序序列。通过这两部分再到先序序列 中找到左右子树的根结点，如此类推，便可唯一得到一棵二叉树。

例如：已知一棵二叉树的先序序列为 EBADCFHG，其中序序列为 ABCDEFGH。下图说明了还原二叉树的过程。

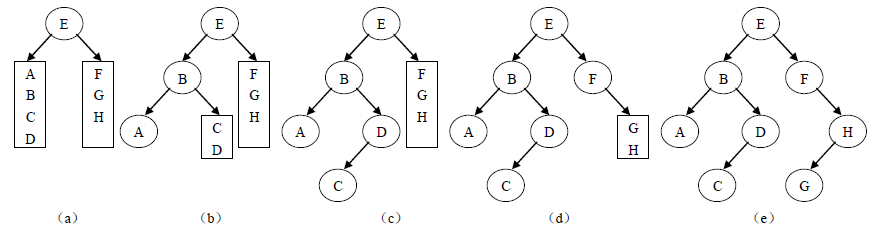
首先由先序序列知道二叉树的根结点为E,则其左子树的中序序列为（ABCD），右子树的中序序列为（FGH）。反过来知道二叉树左子树的先序序列为（BADC），右子树先序序列为（FHG）。然后对二叉树的左右子树分别用先序和中序序列分析其根结点及其左右子树，直到得到整个二叉树结构。

由后序和中序遍历序列还原二叉树：同样，同过二叉树的后序和中序序列也可以唯一确定一棵二叉树。其方法与上述方法类似，只不过此时根结点是出现在后序序列的最后面。

由先序和后序序列不能唯一确定一棵二叉树。例如：先序序列为 AB，后序序列为BA。此时就无法确定二叉树的结构，因为B 既可以是根A 的左子树，也可以是根A 的右子树。

六、 Huffman 树

Huffman 树又称最优树，可以用来构造最优编码，用于信息传输、数据压缩等方面，是一类有着广泛应用的二叉树。

6.1  二叉编码树（实现字符集的不定长编码）

在计算机系统中，符号数据在处理之前首先需要对符号进行二进制编码。例如，在计算机中使用的英文字符的ASCII编码就是8位二进制编码，由于ASCII码使用固定长度的二进制位表示字符，因此 ASCII码是一种定长编码。为了缩短数据编码长度，可以采用不定长编码。其基本思想是：给使用频度较高的字符编较短的编码，这是数据压缩技术的最基本思想。如何给数据中的字符编以不定长编码，而使数据编码的平均长度最短呢？

首先分析第一个问题：如何对字符集进行不定长编码。在一个编码系统中，任何一个编码都不是其他编码的前缀，则称该编码系统的编码是前缀码。例如：01, 10, 110, 111, 101 就不是前缀编码，因为 10 是 101 的前缀，如果去掉 10 或101 就是前缀编码。当在一个编码系统中采用定长编码时，可以不需要分隔符；如果采用不定长编码时，必须使用前缀编码或分隔符，否则在解码时会产生歧义。所谓解码就是由二进制位串还原字符数据的过程。而使用分隔符会加大编码长度，因此一般采用前缀编码。

例6-1 假设字符集为{A, B, C, D}，原文为 ABACCDA。

一种等长编码方案为A:00   B:01 C:10 D:11，此时编解码不会产生歧义，过程如下。

编码：ABACCDA  →  00010010101100

解码：00010010101100  →  ABACCDA

一种不等长编码方案为：A:0         B:00 C:1   D:01，由于此编码不是前缀码，此时在编解码的过程中会产生歧义。对于同一编码可以有不同的解码，过程如下。

编码：ABACCDA  →  000011010

解码：000011010  →  AAAACCDA

      000011010  →  BBCCDA     错误！出现歧义。

 

为产生没有歧义的前缀编码，可以使用二叉编码树来实现。

 为产生没有歧义的前缀编码，可以使用二叉编码树来实现。使用二叉树对字符集中的字符进行编码的方法是，将字符集中的所有字符作为二叉树的叶子结点；在二叉树中，每一个“父亲—左孩子”关系对应一位二进制位0，每一个“父亲—右孩子”关系对应一位二进制位1；于是从根结点通往每个叶子结点的路径，就对应于相应字符的二进制编码。每个字符编码的长度L 等于对应路径的长度，也等于该叶子结点的层次数。

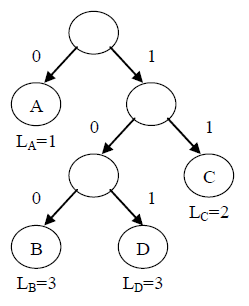
按照上图的二叉编码树对 A、B、C、D 四个字符进行编码，则 A 的编码是 0，B 的编码是 100，C 的编码是 11，D的编码是 101。这个编码显然是一个前缀编码。由于在二叉树中任何一个叶子结点都不会出现在根到其他叶子结点的路径上，那么按照 上述二叉编码树的编码方法，任何一个叶子结点表示的编码都不会是任何其他叶子表示编码的前缀，因此由二叉编码树得到的编码都是前缀码。

反过来如果要进行解码，也可以由二叉编码树便捷的完成。解码的过程是从头开始扫描二进制编码位串，并从二叉编码树的根结点开始，根据比特位不断进入下一层结点，当碰到0 时向左深入，为1 时向右深入；到达叶子结点后输出其对应的字符，然后重新回到根结点， 并继续扫描二进制位串直到完毕。

6.2  Huffman树及Huffman编码

对于同一个字符集进行编码的二叉编码树可以有很多，只要叶子结点个数与字符个数对应即可。在这些不同的编码中哪个才是使得编码长度最小的呢？

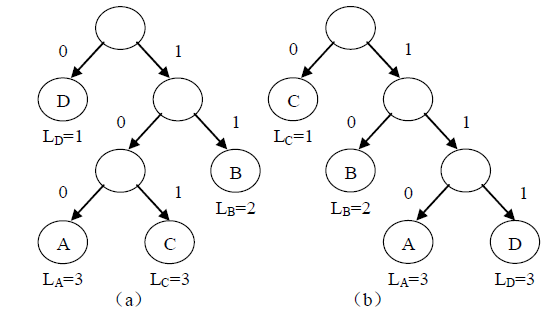
假设字符 A、B、C、D 分别出现了3 次、1 次、2 次、1 次。使用图（a）的编码方案，编码的长度为3×3+1×2+2×3+1×1=18；使用图（b）的编码方案，编码的长度为 3×3+1×2+2×1+1×3=16。

 

字符集中各种字符出现的概率是不同的，字符的出现概率决定了编码方案的选择。

二叉编码树的带权编码长度是衡量一个编码优劣的重要指标，它决定了编码的优劣。要求编码长度最小的编码方案实际上就是寻找带权编码长度最小的二叉编码树。下面将这个问题进一步进行抽象，可以将字符的带权编码长度以及二叉编码树的带权编码长度抽象为一般二叉树中的概念。

给树中的节点赋予一个具有某种意义的正数，我们称之为该结点的权。结点的带权路径长度是从根结点到该结点之间的路径长度与结点权的乘积。树的带权路径长度定义为树中所有叶子结点的带权路径长度之和WPL = ∑WiLi 1≤i≤n

其中：n为叶子结点个数,Wi为第i个叶子结点的权，Li为从根到第i个叶子结点路径的长度。当引入以上概念以后，求最佳编码方案实际上就抽象为求在叶子结点个数与权确定时带权路径长度最小的二叉树。那么什么样的树带权路径长度最小呢？

对于给定n个权值w1, w2, … wn（n≥2），求一棵具有n个叶子结点的二叉树，使其带权路径长度∑WiLi最小。由于Huffman给出了构造具有这种树的方法，因此这种树称为Huffman树。

Huffman树：它是由n个带权叶子结点构成的所有二叉树中带权路径长度最小的二叉树，Huffman 树又称最优二叉树。

构造 Huffman 树的算法步骤如下：

①根据给定的n个权值，构造n棵只有一个根结点的二叉树， n个权值分别是这些二叉树根结点的权，F是由这n棵二叉树构成的集合；

②在F 中选取两棵根结点树值最小的树作为左、右子树，构造一颗新的二叉树，置新二叉树根的权值=左子树根结点权值+右子树根结点权值；

③从F中删除这两颗树，并将新树加入F；

④重复②③，直到F中只含一棵树为止。

直观地看，先选择权值小的，所以权值小的结点被放置在树的较深层，而权值较大的离根较近，这样自然在Huffman树中权越大的叶子离根越近，这样一来，在计算树的带权路径长度时，自然会具有最小的带权路径长度，这种生成算法就是一种典型的贪心算法。

例 6-2假设有一组权值{7, 4, 2, 9, 15, 5}，试构造以这些权值为叶子的 Huffman 树。 构造 Huffman 树的过程如图所示

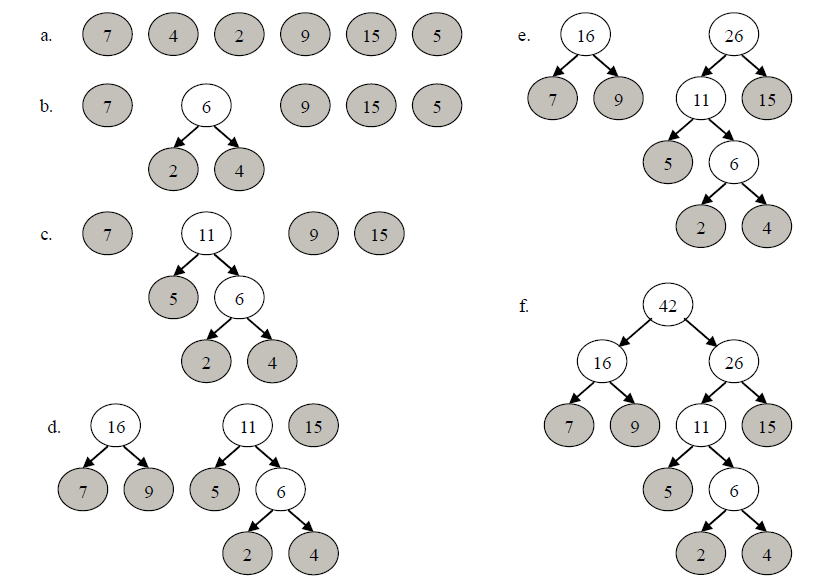
使用二叉编码树进行编码，以字符出现的概率作为相应叶子的权值，当这棵二叉编码树是 Huffman 树时，所得到的编码称之为Huffman编码。

n个叶子构成的哈夫曼树其带权路径长度唯一吗？确实唯一。树形唯一吗？不唯一。因为将森林中两棵权值最小和次小的子棵合并时，哪棵做左子树，哪棵做右子树并不严格限制。上面的做法是把权值较小的当做左子树 , 权值较大的当做右子树。如果反过来也可以，画出的树形有所不同，但 WPL 值相同。为了便于讨论交流在此提倡权值较小的做左子树 , 权值较大的做右子。

6.3  Huffman 树的链式存储结构的实现

Huffman 树也是一棵二叉树，其结点可以继承二叉树的结点来实现，但是需要两个新的属性，即权值和编码。代码 6-2 定义了 Huffman 树的节点结构。

代码 Huffman树结点定义

public class HuffmanTreeNode extends BinTreeNode {

private int weight;     //权值

private Stringcoding = "";    //编码

//构造方法

public HuffmanTreeNode(int weight){  this(weight,null);}

public HuffmanTreeNode(intweight, Object e){

super(e);

this.weight = weight;

 

}

//改写父类方法

public HuffmanTreeNodegetParent() {

return (HuffmanTreeNode)super.getParent();

}

public HuffmanTreeNode getLChild() {

return (HuffmanTreeNode)super.getLChild();

}

public HuffmanTreeNode getRChild() {

return (HuffmanTreeNode)super.getRChild();

}

//get&set方法

public int getWeight(){ return weight;}

public String getCoding(){ returncoding;}

public void setCoding(String coding){ this.coding = coding;}

}

构造 Huffman 树的过程

算法  buildHuffmanTree

//通过结点数组生成 Huffman 树

private static HuffmanTreeNodebuildHuffmanTree(HuffmanTreeNode[] nodes){

int n= nodes.length;

if (n<2) return nodes[0];

List l = new ListArray(); //根结点线性表，按 weight 从大到小有序

for (int i=0; i<n;i++) //将结点逐一插入线性表

insertToList(l,nodes[i]);

for (int i=1; i<n; i++){   //选择weight 最小的两棵树合并，循环 n-1 次 HuffmanTreeNodemin1 = (HuffmanTreeNode)l.remove(l.getSize()-1);

HuffmanTreeNode min2= (HuffmanTreeNode)l.remove(l.getSize()-1); HuffmanTreeNode newRoot =new HuffmanTreeNode(min1.getWeight()+min2.getWeight());newRoot.setLChild(min1);                newRoot.setRChild(min2); //合并insertToList(l,newRoot);//新树插入线性表

}                                                                  

return(HuffmanTreeNode)l.get(0);//返回 Huffman 树的根

}

//将结点按照 weight 从大到小的顺序插入线性表

private static void insertToList(List l, HuffmanTreeNode node){

for (intj=0; j<l.getSize();j++)

if (node.getWeight()>((HuffmanTreeNode)l.get(j)).getWeight()){

l.insert(j,node);                                          

return;                                                    

 

}                                                               

l.insert(l.getSize(),node);

}

Huffman 编码可以在Huffman树中递归生成，

算法generateHuffmanCode,输入：Huffman 树根结点 输出：生成 Huffman 编码代码：

//递归生成 Huffman 编码

private static void generateHuffmanCode(HuffmanTreeNode root){

if (root==null) return;

if (root.hasParent()){

if (root.isLChild())

root.setCoding(root.getParent().getCoding() + "0");              //向左为 0

else                                                            

root.setCoding(root.getParent().getCoding() + "1");              //向右为1

}                                 generateHuffmanCode(root.getLChild());generateHuffmanCode(root.getRChild());

}

 

6.4. 哈夫曼树的应用

6.4.1用于最佳判断过程。

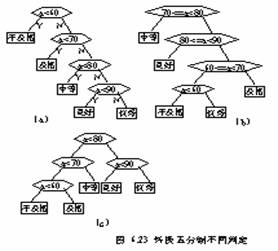
在考查课记分时往往把百分制转换成优（ x>=90 ）、良 (80<x<90) 、中 (70<=x80) 、及格 (60<=x<70) 、不及格 (x<60) 五个等级。若不考虑学生考试分数的分布概率，程序判定过程很容易写成图 6.23(a) 所示的方法。我们知道，一般来讲学生考分大多分布在 70 至 80 分之间，从图 6.23(a) 可看出这种情的 x 值要比较 2 至 3 次才能确定等级。而学生中考试不及格的人数很少， x 值比较一次即可定等级。能否使出现次数多的在 70 至 80 分之间的 x 值比较次数减少些，而使很少出现的低于 60 分的 x 值比较次数多一些，以便提高程序的运行效率呢？假设学生成绩对于不及格、及格、中等、良好和优秀的分布概率分别为 5 ％， 15 ％， 40 ％， 30 ％， 10 ％，以它们做为叶子的权值来构造哈夫曼树，如图 6.23(b) 所示。此时带权路径长最短，其值为 205 ％。它可以使大部分的分数值经过较少的比较次数得到相应的等级。但是，事务往往不是绝对的，此时每个判断柜内的条件较为复杂，比较两次，反而降低运行效率。所以我们采用折衷作法，调整后得图 6.23(c) 判定树。它更加切合实际。

 

6.4.2用于通信编码

在通信及数据传输中多采用二进制编码。为了使电文尽可能的缩短，可以对电文中每个字符出现的次数进行统计。设法让出现次数多的字符的二进制码短些，而让那些很少出现的字符的二进制码长一些。假设有一段电文，其中用到 4 个不同字符Ａ，Ｃ，Ｓ，Ｔ，它们在电文中出现的次数分别为 7 ，2 ，4 ，5 。把 7 ，2 ，4 ，5 当做 4 个叶子的权值构造哈夫曼树如图所示。在树中令所有左分支取编码为 0 ，令所有右分支取编码为1。将从根结点起到某个叶子结点路径上的各左、右分支的编码顺序排列，就得这个叶子结点所代表的字符的二进制编码，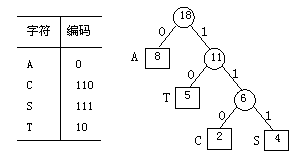

关于信息编码是一个复杂的问题，还应考虑其他一些因素。比如前缀编码每个编码的长度不相等，译码时较困难。还有检测、纠错问题都应考虑在内。这里仅对哈夫曼树举了一个应用实例。

谷歌2013校园招聘笔试题

1.5 用二进制来编码字符串“abcdabaa”，需要能够根据编码，解码回原来的字符串，最少需要多长的二进制字符串？

  A.12 B.14 C.18 D.24