数据结构---->线性表
线性表
一、线性表抽象数据类型
1.1、定义
线性表是指n (n>=0)个相同类型的数据元素a0,a1,...an-1所构成的有限线性序列,其一般描述为:LinearList=(a0,a1,…,an-1)
1) 其中LinearList称为线性表的名称
2) 每个ai(n-1≥i≥0)称为线性表的数据元素,可以是整数、浮点数、字符或类
3) 表中相邻元素之间存在着顺序关系:将ai-1称为ai的直接前趋,ai+1称为ai的直接后继
4) 具体n的值称为线性表中包含有数据元素的个数,也称为线性表的长度
5) 当n的值等于0时,表示该线性表是空表
离散定义如下:B=<A,R>,其中A包含n个结点的集合(a0,a1,…an-1),R是关系的集合{(ai-1,ai)|i=1,2,..n},可见R只有一种类型的关系,即线性关系。
抽象数据类型定义如下:
ADT LinearList
{
数据对象:D={ai|ai∈元素集合,i=0,1,2,..n-1 n>=0}
数据关系:R={<ai-1,ai>|ai-1,ai∈元素集合,i=1,2,..n}
基本操作:{插入,删除,查找等}
} ADT LinearList
1.2、线性表接口
package LinearList;
import util.OutOfBoundaryException;
public interface LinearList {
// 返回线性表的大小,即数据元素的个数。
public int getSize();
// 如果线性表为空返回true,否则返回false。
public boolean isEmpty();
// 判断线性表是否包含数据元素e
public boolean contains(Object e);
// 返回数据元素e 在线性表中的序号
public int indexOf(Object e);
// 将数据元素e 插入到线性表中i 号位置
public void insert(int i, Object e) throws OutOfBoundaryException;
// 将数据元素e 插入到元素obj 之前
public boolean insertBefore(Object obj, Object e);
// 将数据元素e 插入到元素obj 之后
public boolean insertAfter(Object obj, Object e);
// 删除线性表中序号为i 的元素,并返回之
public Object remove(int i) throws OutOfBoundaryException;
// 删除线性表中第一个与e 相同的元素
public boolean remove(Object e);
// 替换线性表中序号为i 的数据元素为e,返回原数据元素
public Object replace(int i, Object e) throws OutOfBoundaryException;
// 返回线性表中序号为i 的数据元素
public Object get(int i) throws OutOfBoundaryException;
}
附两个接口(下面的代码会用的到)
线性表序号越界异常
package util;
//线性表中出现序号越界时抛出该异常
public class OutOfBoundaryException extends RuntimeException {
public OutOfBoundaryException(String err) {
super(err);
}
}
线性表中比较元素是否相等及大小判断(类似于comparable接口,indexOf()、contains()方法会用得到)
package util;
public interface Strategy {
// 判断两个数据元素是否相等
public boolean equal(Object obj1, Object obj2);
// 比较两个数据元素的大小 如果obj1 < obj2 返回-1 如果obj1 = obj2 返回0 35 如果obj1 > obj2 返回1
public int compare(Object obj1, Object obj2);
}
线性表有两种存储方式,对应地把线性表分成了两类:
顺序存储结构的顺序表(或称向量存储、一维数组存储)
链式存储结构的链表
二、线性表的顺序表示和实现
顺序表:用顺序存储方法存储的线性表简称为顺序表
public class SeqList<T> implements LinearList<T> //顺序表类
2.1顺序存储方法:
即用一组连续的内存单元依次存放线性表中的数据元素(元素在内存的物理存储次序与它们在线性表中的逻辑次序相同)。在内存中开辟一片连续存储空间,但该连续存储空间的大小要大于或等于顺序表的长度,然后让线性表中第一个元素存放在连续存储空间第一个位置,第二个元素紧跟着第一个之后,其余依此类推

LOC(ai) = LOC(a0) + i×K
其中LOC(a0)为0 号元素a0的存储地址,通常称为线性表的起始地址。
通常利用一维数组来表示顺序表的数据存储区域,这是因为数组具有如下特点:
1) 数据中的元素间的地址是连续的
2) 数组中所有元素的数据类型是相同的
3) 这与线性表的顺序存储结构(顺序表)是类似的
2.2、线性表的数组实现
package sequence_Linear_List;
import util.OutOfBoundaryException;
import util.Strategy;
import LinearList.LinearList;
//线性表的顺序存储
public class SeqList implements LinearList {
private final int LEN = 8; // 数组的默认大小
private Strategy strategy; // 数据元素比较策略
private int size; // 线性表中数据元素的个数
private Object[] elements; // 数据元素数组
// 构造方法
public SeqList() {
// this(new DefaultStrategy());
}
public SeqList(Strategy strategy) {
this.strategy = strategy;
size = 0;
elements = new Object[LEN];
}
// 返回线性表的大小,即数据元素的个数。
public int getSize() {
return size;
}
// 如果线性表为空返回true,否则返回false。
public boolean isEmpty() {
return size == 0;
}
// 判断线性表是否包含数据元素e
public boolean contains(Object e) {
for (int i = 0; i < size; i++)
if (strategy.equal(e, elements[i]))
return true;
return false;
}
// 返回数据元素e 在线性表中的序号
public int indexOf(Object e) {
for (int i = 0; i < size; i++)
if (strategy.equal(e, elements[i]))
return i;
return -1;
}
// 将数据元素e 插入到线性表中i 号位置
public void insert(int i, Object e) throws OutOfBoundaryException {
if (i < 0 || i > size)
throw new OutOfBoundaryException("错误,指定的插入序号越界。");
if (size >= elements.length)
expandSpace();
for (int j = size; j > i; j--)
elements[j] = elements[j - 1];
elements[i] = e;
size++;
return;
}
private void expandSpace() {
Object[] a = new Object[elements.length * 2];
for (int i = 0; i < elements.length; i++)
a[i] = elements[i];
elements = a;
}
// 将数据元素e 插入到元素obj 之前
public boolean insertBefore(Object obj, Object e) {
int i = indexOf(obj);
if (i < 0)
return false;
insert(i, e);
return true;
}
// 将数据元素e 插入到元素obj 之后
public boolean insertAfter(Object obj, Object e) {
int i = indexOf(obj);
if (i < 0)
return false;
insert(i + 1, e);
return true;
}
// 删除线性表中序号为i 的元素,并返回之
public Object remove(int i) throws OutOfBoundaryException {
if (i < 0 || i >= size)
throw new OutOfBoundaryException("错误,指定的删除序号越界。");
Object obj = elements[i];
for (int j = i; j < size - 1; j++)
elements[j] = elements[j + 1];
elements[--size] = null;
return obj;
}
// 删除线性表中第一个与e 相同的元素
public boolean remove(Object e) {
int i = indexOf(e);
if (i < 0)
return false;
remove(i);
return true;
}
// 替换线性表中序号为i 的数据元素为e,返回原数据元素
public Object replace(int i, Object e) throws OutOfBoundaryException {
if (i < 0 || i >= size)
throw new OutOfBoundaryException("错误,指定的序号越界。");
Object obj = elements[i];
elements[i] = e;
return obj;
}
// 返回线性表中序号为i 的数据元素
public Object get(int i) throws OutOfBoundaryException {
if (i < 0 || i >= size)
throw new OutOfBoundaryException("错误,指定的序号越界。");
return elements[i];
}
}
三、线性表的链式表示和实现
实现线性表的另一种方法是链式存储,即用指针将存储线性表中数据元素的那些单元依次串联在一起。这种方法避免了在数组中用连续的单元存储元素的缺点,因而在执行插入或删除运算时,不再需要移动元素来腾出空间或填补空缺。然而我们为此付出的代价是,需要在每个单元中设置指针来表示表中元素之间的逻辑关系,因而增加了额外的存储空间的开销。
首先给出各种接口,下面的单链表和双向链表实现类中会用到。
链表的节点接口:
package linked_list;
public interface Node {
// 获取结点数据域
public Object getData();
// 设置结点数据域
public void setData(Object obj);
}
迭代器接口 Iterator:提供一种方法顺序访问一个聚集对象中各个元素,而又不需暴露该对象的内部表示。(java也有)
package util;
public interface Iterator {
// 移动到第一个元素
public void first();
// 移动到下一个元素
public void next();
// 检查迭代器中是否还有剩余的元素
public boolean isDone();
// 返回当前元素
public Object currentItem();
}
链接表的迭代实现类
package linked_list;
import util.Iterator;
import util.OutOfBoundaryException;
public class LinkedListIterator implements Iterator {
private LinkedList list;// 链接表
private Node current;// 当前结点
// 构造方法
public LinkedListIterator(LinkedList list) {
this.list = list;
if (list.isEmpty()) // 若列表为空
current = null; // 则当前元素置空
else
current = list.first();// 否则从第一个元素开始
}
// 移动到第一个元素
public void first() {
if (list.isEmpty()) // 若列表为空
current = null; // 则当前元素置空
else
current = list.first();// 否则从第一个元素开始
}
// 移动到下一个元素
public void next() throws OutOfBoundaryException {
if (isDone())
throw new OutOfBoundaryException("错误:已经没有元素。");
if (current == list.last())
current = null; // 当前元素后面没有更多元素
else
current = list.getNext(current);
}
// 检查迭代器中是否还有剩余的元素
public boolean isDone() {
return current == null;
}
// 返回当前元素
public Object currentItem() throws OutOfBoundaryException {
if (isDone())
throw new OutOfBoundaryException("错误:已经没有元素。");
return current.getData();
}
}
InvalidNodeException类
package util;
//InvalidNodeException 异常
public class InvalidNodeException extends RuntimeException {
public InvalidNodeException(String err) {
super(err);
}
}
3.1单链表

单链表结点定义
package single_Linked_LinerList;
public class SLNode {
private Object element;
private SLNode next;
public SLNode() {
this(null, null);
}
public SLNode(Object ele, SLNode next) {
this.element = ele;
this.next = next;
}
public SLNode getNext() {
return next;
}
public void setNext(SLNode next) {
this.next = next;
}
/**************** Methods of Node Interface **************/
public Object getData() {
return element;
}
public void setData(Object obj) {
element = obj;
}
}
线性表的单链表实现(基于数据或者序号的操作)
package single_Linked_LinerList;
import util.OutOfBoundaryException;
import util.Strategy;
import LinearList.LinearList;
//线性表的单链表实现
public class SingleLinkedList implements LinearList {
private Strategy strategy; // 数据元素比较策略
private SLNode head; // 单链表首结点引用
private int size; // 线性表中数据元素的个数
public SingleLinkedList() {
// this(new DefaultStrategy());
}
public SingleLinkedList(Strategy strategy) {
this.strategy = strategy;
head = new SLNode();
size = 0;
}
// 辅助方法:获取数据元素e 所在结点的前驱结点
private SLNode getPreNode(Object e) {
SLNode p = head;
while (p.getNext() != null)
if (strategy.equal(p.getNext().getData(), e))
return p;
else
p = p.getNext();
return null;
}
// 辅助方法:获取序号为0<=i<size 的元素所在结点的前驱结点
private SLNode getPreNode(int i) {
SLNode p = head;
for (; i > 0; i--)
p = p.getNext();
return p;
}
// 获取序号为0<=i<size 的元素所在结点
private SLNode getNode(int i) {
SLNode p = head.getNext();
for (; i > 0; i--)
p = p.getNext();
return p;
}
// 返回线性表的大小,即数据元素的个数。
public int getSize() {
return size;
}
// 如果线性表为空返回true,否则返回false。
public boolean isEmpty() {
return size == 0;
}
// 判断线性表是否包含数据元素e
public boolean contains(Object e) {
SLNode p = head.getNext();
while (p != null)
if (strategy.equal(p.getData(), e))
return true;
else
p = p.getNext();
return false;
}
// 返回数据元素e 在线性表中的序号
public int indexOf(Object e) {
SLNode p = head.getNext();
int index = 0;
while (p != null)
if (strategy.equal(p.getData(), e))
return index;
else {
index++;
p = p.getNext();
}
return -1;
}
// 将数据元素e 插入到线性表中i 号位置
public void insert(int i, Object e) throws OutOfBoundaryException {
if (i < 0 || i > size)
throw new OutOfBoundaryException("错误,指定的插入序号越界。");
SLNode p = getPreNode(i);
SLNode q = new SLNode(e, p.getNext());
p.setNext(q);
size++;
return;
}
// 将数据元素e 插入到元素obj 之前
public boolean insertBefore(Object obj, Object e) {
SLNode p = getPreNode(obj);
if (p != null) {
SLNode q = new SLNode(e, p.getNext());
p.setNext(q);
size++;
return true;
}
return false;
}
// 将数据元素e 插入到元素obj 之后
public boolean insertAfter(Object obj, Object e) {
SLNode p = head.getNext();
while (p != null)
if (strategy.equal(p.getData(), obj)) {
SLNode q = new SLNode(e, p.getNext());
p.setNext(q);
size++;
return true;
} else
p = p.getNext();
return false;
}
// 删除线性表中序号为i 的元素,并返回之
public Object remove(int i) throws OutOfBoundaryException {
if (i < 0 || i >= size)
throw new OutOfBoundaryException("错误,指定的删除序号越界。");
SLNode p = getPreNode(i);
Object obj = p.getNext().getData();
p.setNext(p.getNext().getNext());
size--;
return obj;
}
// 删除线性表中第一个与e 相同的元素
public boolean remove(Object e) {
SLNode p = getPreNode(e);
if (p != null) {
p.setNext(p.getNext().getNext());
size--;
return true;
}
return false;
}
// 替换线性表中序号为i 的数据元素为e,返回原数据元素
public Object replace(int i, Object e) throws OutOfBoundaryException {
if (i < 0 || i >= size)
throw new OutOfBoundaryException("错误,指定的序号越界。");
SLNode p = getNode(i);
Object obj = p.getData();
p.setData(e);
return obj;
}
// 返回线性表中序号为i 的数据元素
public Object get(int i) throws OutOfBoundaryException {
if (i < 0 || i >= size)
throw new OutOfBoundaryException("错误,指定的序号越界。");
SLNode p = getNode(i);
return p.getData();
}
}
3.2基于结点的操作
线性表抽象数据类型中,其提供的操作主要是指对线性表中的数据元素及其序号的。例如插入作就是基于序号和元素进行的,insert(i,e)是在序号为i 的地方插入元素,insertBefore 、与insertAfter 是在某个数据元素之前或之后插入新的元素。这种基于序号的操作实际上并不适合采用(单向或双向)链表来实现,因为为了在链表中定位数据元素或序号,我们不得不沿着结点间的next(或pre)引用,从链表前端(双向链表也可以从后端)开始逐一扫描。
我们考察一种经常需要完成的操作:顺序的将线性表中每个数据元素都访问一遍。如果使用链式存储实现的线性表ListSLinked所提供的get(i)操作来实现,则需要Ο(n2)时间。因为在使用链表实现取i号数据元素的操作时,需要将结点的引用从链表前端向后移动i次,而取i+1 号数据元素时不能在上一次操作——取i号数据元素——的过程中受益,而必须重新从链表前端开始定位,则访问线性表中每个元素一次所需要的总时间为0+1+2+…+n-1=Ο(n2)。这一时间复杂度是难以接受的。
实际上,除了通过序号来访问线性结构中的元素,还可通过其他途径来得到线性结构中的元素。例如我们能够直接通过结点来访问数据元素,通过3.3.1 中定义的结点接口,我们看到结点实际上可以看成是可以存取数据元素的容器,数据元素与存放它的容器是一一对应的。如果能够取得结点的引用,则可以取得相应结点存储的数据元素,并且在实际应用中的许多情况下更希望以结点作为参数来完成某些操作。如果能够以结点作为参数,那么就可以在Ο(1)时间内定位结点的地址,进而可以在更短的时间内完成相应的操作。例如如果能够直接定位在链表中进行插入和删除结点的前驱,那么相应的插入和删除操作都可以在Ο(1)完成。
3.3链表接口(基于结点)
(初始化、为空、为满、返回长度、get、set、查找、插入、删除、置空、遍历、前驱、后继)
package linked_list;
import util.InvalidNodeException;
import util.Iterator;
import util.OutOfBoundaryException;
//链接表接口
public interface LinkedList {
// 查询链接表当前的规模
public int getSize();
// 判断列表是否为空
public boolean isEmpty();
// 返回第一个结点
public Node first() throws OutOfBoundaryException;
// 返回最后一结点
public Node last() throws OutOfBoundaryException;
// 返回p 之后的结点
public Node getNext(Node p) throws InvalidNodeException,
OutOfBoundaryException;
// 返回p 之前的结点
public Node getPre(Node p) throws InvalidNodeException,
OutOfBoundaryException;
// 将e 作为第一个元素插入链接表,并返回e 所在结点
public Node insertFirst(Object e);
// 将e 作为最后一个元素插入列表,并返回e 所在结点
public Node insertLast(Object e);
// 将e 插入至p 之后的位置,并返回e 所在结点
public Node insertAfter(Node p, Object e) throws InvalidNodeException;
// 将e 插入至p 之前的位置,并返回e 所在结点
public Node insertBefore(Node p, Object e) throws InvalidNodeException;
// 删除给定位置处的元素,并返回之
public Object remove(Node p) throws InvalidNodeException;
// 删除首元素,并返回之
public Object removeFirst() throws OutOfBoundaryException;
// 删除末元素,并返回之
public Object removeLast() throws OutOfBoundaryException;
// 将处于给定位置的元素替换为新元素,并返回被替换的元素
public Object replace(Node p, Object e) throws InvalidNodeException;
// 元素迭代器
public Iterator elements();
}
3.4双向链表
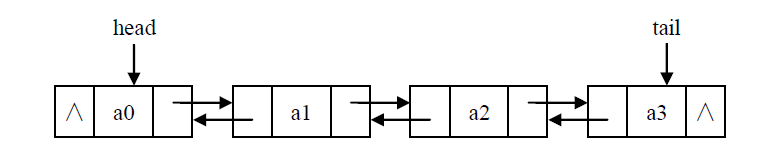
双向链表节点定义
package double_linked_list;
import linked_list.Node;
//双向链表结点定义
public class DLNode implements Node {
private Object element;
private DLNode pre;
private DLNode next;
public DLNode() {
this(null, null, null);
}
public DLNode(Object ele, DLNode pre, DLNode next) {
this.element = ele;
this.pre = pre;
this.next = next;
}
public DLNode getNext() {
return next;
}
public void setNext(DLNode next) {
this.next = next;
}
public DLNode getPre() {
return pre;
}
public void setPre(DLNode pre) {
this.pre = pre;
}
/**************** Node Interface Method **************/
public Object getData() {
return element;
}
public void setData(Object obj) {
element = obj;
}
}
双向链表实现(基于节点的操作)
package double_linked_list;
import util.InvalidNodeException;
import util.Iterator;
import util.OutOfBoundaryException;
import linked_list.LinkedList;
import linked_list.LinkedListIterator;
import linked_list.Node;
//基于双向链表实现的链接表
public class Double_linked_list implements LinkedList {
private int size; // 规模
private DLNode head;// 头结点,哑元结点
private DLNode tail;// 尾结点,哑元结点
public Double_linked_list() {
size = 0;
head = new DLNode();// 构建只有头尾结点的链表
tail = new DLNode();
head.setNext(tail);
tail.setPre(head);
}
// 辅助方法,判断结点p 是否合法,如合法转换为DLNode
protected DLNode checkPosition(Node p) throws InvalidNodeException {
if (p == null)
throw new InvalidNodeException("错误:p 为空。");
if (p == head)
throw new InvalidNodeException("错误:p 指向头节点,非法。");
if (p == tail)
throw new InvalidNodeException("错误:p 指向尾结点,非法。");
DLNode node = (DLNode) p;
return node;
}
// 查询链接表当前的规模
public int getSize() {
return size;
}
// 判断链接表是否为空
public boolean isEmpty() {
return size == 0;
}
// 返回第一个结点
public Node first() throws OutOfBoundaryException {
if (isEmpty())
throw new OutOfBoundaryException("错误:链接表为空。");
return head.getNext();
}
// 返回最后一结点
public Node last() throws OutOfBoundaryException {
if (isEmpty())
throw new OutOfBoundaryException("错误:链接表为空。");
return tail.getPre();
}
// 返回p 之后的结点
public Node getNext(Node p) throws InvalidNodeException,
OutOfBoundaryException {
DLNode node = checkPosition(p);
node = node.getNext();
if (node == tail)
throw new OutOfBoundaryException("错误:已经是链接表尾端。");
return node;
}
// 返回p 之前的结点
public Node getPre(Node p) throws InvalidNodeException,
OutOfBoundaryException {
DLNode node = checkPosition(p);
node = node.getPre();
if (node == head)
throw new OutOfBoundaryException("错误:已经是链接表前端。");
return node;
}
// 将e 作为第一个元素插入链接表
public Node insertFirst(Object e) {
DLNode node = new DLNode(e, head, head.getNext());
head.getNext().setPre(node);
head.setNext(node);
size++;
return node;
}
// 将e 作为最后一个元素插入列表,并返回e 所在结点
public Node insertLast(Object e) {
DLNode node = new DLNode(e, tail.getPre(), tail);
tail.getPre().setNext(node);
tail.setPre(node);
size++;
return node;
}
// 将e 插入至p 之后的位置,并返回e 所在结点
public Node insertAfter(Node p, Object e) throws InvalidNodeException {
DLNode node = checkPosition(p);
DLNode newNode = new DLNode(e, node, node.getNext());
node.getNext().setPre(newNode);
node.setNext(newNode);
size++;
return newNode;
}
// 将e 插入至p 之前的位置,并返回e 所在结点
public Node insertBefore(Node p, Object e) throws InvalidNodeException {
DLNode node = checkPosition(p);
DLNode newNode = new DLNode(e, node.getPre(), node);
node.getPre().setNext(newNode);
node.setPre(newNode);
size++;
return newNode;
}
// 删除给定位置处的元素,并返回之
public Object remove(Node p) throws InvalidNodeException {
DLNode node = checkPosition(p);
Object obj = node.getData();
node.getPre().setNext(node.getNext());
node.getNext().setPre(node.getPre());
size--;
return obj;
}
// 删除首元素,并返回之
public Object removeFirst() throws OutOfBoundaryException {
return remove(head.getNext());
}
// 删除末元素,并返回之
public Object removeLast() throws OutOfBoundaryException {
return remove(tail.getPre());
}
// 将处于给定位置的元素替换为新元素,并返回被替换的元素
public Object replace(Node p, Object e) throws InvalidNodeException {
DLNode node = checkPosition(p);
Object obj = node.getData();
node.setData(e);
return obj;
}
// 元素迭代器
public Iterator elements() {
return new LinkedListIterator(this);
}
}
3.5 单向循环链表
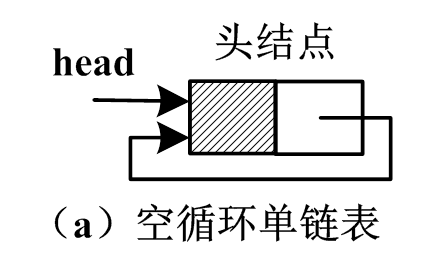
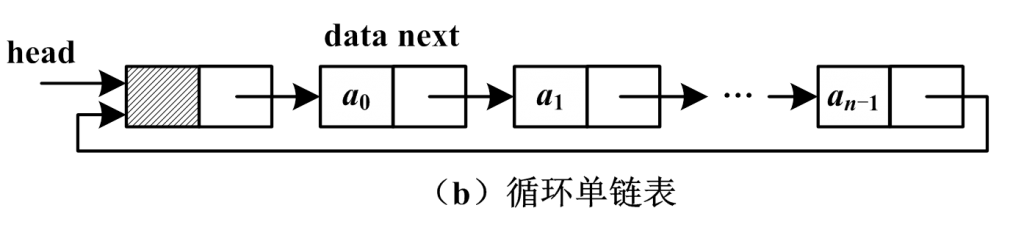
3.6 双向循环链表

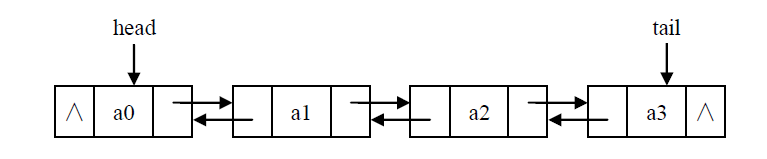
四、两种实现的对比
4.1 基于时间的比较
线性表的操作主要有查找、插入、删除三类操作。对于查找操作有基于序号的查找,即存取线性表中i 号数据元素。由于数组有随机存取的特性,在线性表的顺序存储实现中可以在Θ(1)的时间内完成;而在链式存储中由于需要从头结点开始顺着链表才能取得,无法在常数时间内完成,因此顺序存储优于链式存储。查找操作还有基于元素的查找,即线性表是否包含某个元素、元素的序号是多少,这类操作线性表的顺序存储与链式存储都需要从线性表中序号为0 的元素开始依次查找,因此两种实现的性能相同。综上所述,如果在线性表的使用中主要操作是查找,那么应当选用顺序存储实现的线性表。
对于基于数据元素的插入、删除操作而言,当使用数组实现相应操作时,首先需要采用顺序查找定位相应数据元素,然后才能插入、删除,并且在插入、删除过程又要移动大量元素;相对而言链表的实现只需要在定位数据元素的基础上,简单的修改几个指针即可完成,因此链式存储优于顺序存储。对于基于序号的插入、删除操作,因为在顺序存储中平均需要移动一半元素;而在链式存储中不能直接定位,平均需要比较一半元素才能定位。因此顺序存储与链式存储性能相当。综上所述,如果在线性表的使用中主要操作是插入、删除操作,那么选用链式存储的线性表为佳。
4.2 基于空间的比较
线性表的顺序存储,其存储空间是预先静态分配的,虽然在实现的过程中可以动态扩展数组空间,但是如果线性表的长度变化范围较大,空间在使用过程中由于会存在大量空闲空间,使得存储空间的利用率不高。而线性表的链式存储,其结点空间是动态分配的,不会存在存储空间没有完全利用的情况。因此当线性表长度变化较大时,宜采用链式存储结构。当线性表的数据元素结构简单,并且线性表的长度变化不大时。由于链式存储结构使用了额外的存储空间来表示数据元素之间的逻辑关系,因此针对数据域而言,指针域所占比重较大;而在线性表的顺序存储结构中,没有使用额外的存储空间来表示数据元素之间的逻辑关系,尽管有一定的空闲空间没有利用,但总体而言由于线性表长度变化不大,因此没有利用的空间所占比例较小。所以当线性表数据元素结构简单,长度变化不大时可以考虑采用顺序存储结构。
顺序存储的优点是存储密度大(=1),存储空间利用率高。缺点是插入或删除元素时不方便。 链式存储的优点是插入或删除元素时很方便,使用灵活。缺点是存储密度小(<1),存储空间利用率低。事实上,链表插入、删除运算的快捷是以空间代价来换取时间。顺序表适宜于做查找这样的静态操作;链表宜于做插入、删除这样的动态操作。若线性表的长度变化不大,且其主要操作是查找,则采用顺序表;若线性表的长度变化较大,且其主要操作是插入、删除操作,则采用链表。
五、线性表的应用:
5.1、多项式的表示及运算
![]()
顺序存储
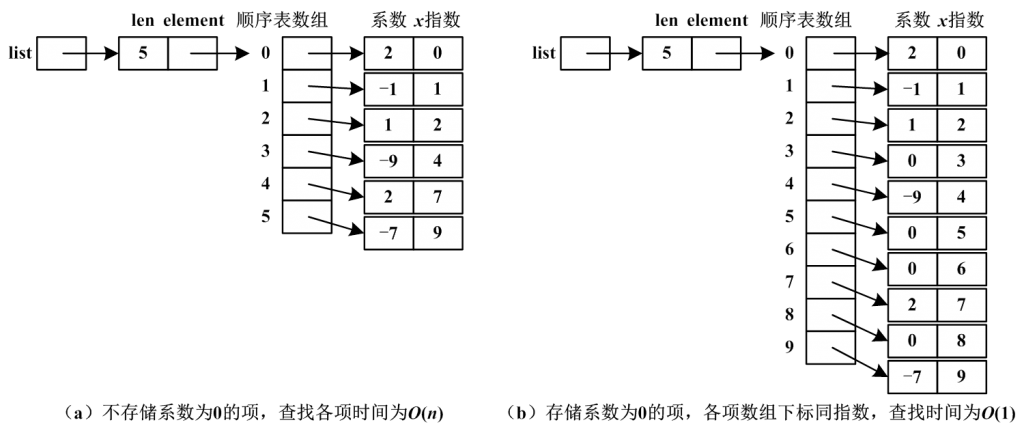
链式存储
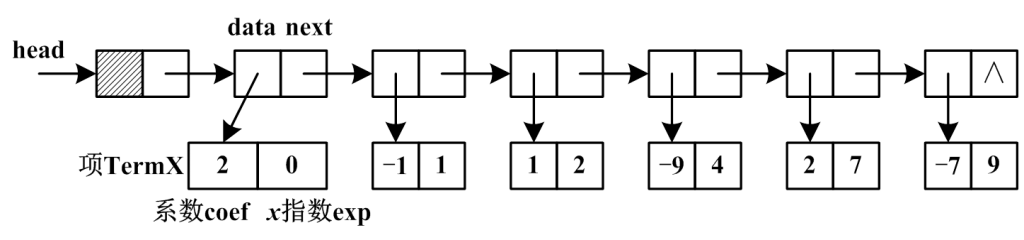
5.2、多项式加减乘(链式存储的实现)
item.java
//多项式的项
public class item {
private float coef; //系数
private int exponent; //幂
private item next;
item(float d, int exp) {
this.coef = d;
this.exponent = exp;
this.next = null;
}
item() {
this.exponent = 0;
this.next = null;
}
item(float d) {
this.coef = d;
this.exponent = 0;
this.next = null;
}
public float getcoef() {
return coef;
}
public int getexp() {
return exponent;
}
public item getnext() {
return next;
}
public void setcoef(float d) {
this.coef = d;
}
public void setexp(int exp) {
this.exponent = exp;
}
public void setnext(item n) {
this.next = n;
}
public void print() {
String s="";
System.out.print(s + this.coef + "X" + this.exponent);
if (this.next != null)
{
System.out.print("+");
next.print();
}
}
}
poly.java
//多项式
public class poly {
private int count;
private item head;
private item tail;
poly() {
count = 0;
head = null;
tail = null;
}
poly(float c, int exp) {
item i = new item(c, exp);
head = i;
tail = i;
count++;
}
public item gethead() {
return head;
}
public item gettail() {
return tail;
}
public int getcount() {
return count;
}
// 多项式加
public void addpoly(float c) {
item it = new item(c);
addpoly(it);
}
public void addpoly(float c, int exp) {
item it = new item(c, exp);
addpoly(it);
}
public void addpoly(item it) {
item prev = head;
item p = head;
float c = it.getcoef(); // 要添加的项的系数
int exp = it.getexp(); // 要添加的项的幂
if (prev == null) { // 当前的多项式为空,则直接多项式的头尾指针都指向该项
head = it;
tail = it;
} else {
do {
if (prev.getexp() < exp) { // 当前项的幂小于要添加的项
p = prev;
prev = prev.getnext();
} else if (prev.getexp() == exp) { // 当前项的幂等于要添加的项
prev.setcoef(prev.getcoef() + c); // 系数相加
if (prev.getcoef() == 0) { // 系数相加后结果为0,则删除结果项
if (prev == head) { // 结果项在表达式头部,头指针指向下一项
head = prev.getnext();
} else if (prev.getnext() == null) { // 结果项在表达式尾部,尾指针指向前一项
tail = p;
} else {
p.setnext(prev.getnext()); // 结果项在表达式中间,删除该项
}
}
break;
} else if (prev.getexp() > exp) { // 当前项的幂大于要添加的项
if (prev == head) {
head = it;
it.setnext(prev);
break;
} else {
p.setnext(it);
it.setnext(prev);
break;
}
}
} while (prev != null);
if (p.getexp() < exp) {
p.setnext(it);
tail = it;
}
}
count++;
}
public void addpoly(poly p) {
item prev = p.gethead();
do {
addpoly(prev);
prev = prev.getnext();
} while (prev != null);
}
// 多项式减
public void subtractPoly(poly p) {
item prev = p.gethead();
do {
prev.setcoef(0 - prev.getcoef());
addpoly(prev);
prev = prev.getnext();
} while (prev != null);
}
// 多项式乘
public void multiplyPoly(poly p) {
item prev = head;
item pp = p.gethead();
poly pt = new poly();
do {
do {
item temp = new item();
temp.setcoef(prev.getcoef() * pp.getcoef());
temp.setexp(prev.getexp() + pp.getexp());
pt.addpoly(temp);
prev = prev.getnext();
} while (prev != null);
pp = pp.getnext();
} while (pp != null);
head = pt.gethead();
}
public void printpoly() {
item prev = head;
prev.print();
}
}
测试
//使用多项式
public class usepoly {
public static void main(String[] arg) throws Exception {
poly pl = new poly();
poly p2 = new poly();
pl.addpoly(12, 3);
pl.addpoly(4, 9);
pl.addpoly(3, 4);
p2.addpoly(1, 2);
pl.multiplyPoly(p2);
pl.printpoly();
}
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律