广场铺砖问题(状压DP入门)

①前置知识:

　　  ①:按位取与(&) : 0 & 0 = 0 , 0 & 1 = 0 , 1 & 0 = 0 , 1 & 1 =1.

　　②:按位取或( | ): 0 | 0 =0 , 0 | 1 =1 , 1 | 0 = 1 , 1 | 1 = 1.

　　③:按位取异或( ^ ): 0 ^ 1 = 1 , 1 ^ 1 = 0 , 0 ^ 0 = 0 , 1 ^ 0 = 1.

②题面:

　　有一个 W 行 H 列的广场,需要用 1*2 小砖铺盖,小砖之间互相不能重叠,问有多少种不同的铺法?

　　样例输入: 2 4　　样例输出: 5

　　

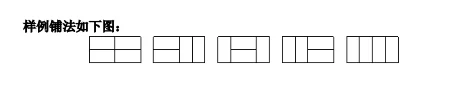
③题目解决:

　　①之前对状压DP不太了解,蒟蒻看到题面的第一眼想到的是线性递推.设F[ i ][ j ]为大小为 i * j的矩阵的铺盖方案,F[ i ][ j ]由F[ i -1][ j ],F[ i-2 ][  j  ],F[ i ][ j - 1],F[ i ][ j -2]转移而来,即在行与列上讨论竖放与横放,并且要根据行与列的奇偶性判断方案转移的合法性.蒟蒻认为DP的转移思路没错,但转移无法对状态判重,会使ans变大.

　　②在听了大佬的讲解后,蒟蒻发现很多问题本质上都是两种对立或相关连的状态构成,正好符合二进制0/1状态,对于这类问题可以用二进制串表示状态.对于这一题,我们设横放的状态为" 0 0 ",对于竖放的设上面的为' 1 ',下面的为' 0 ',显然这一行的摆放状态会影响下一行的拜访状态,所以利用行进行状态转移.

　　③怎么判断转移两个状态的合法性?首先考虑在相邻两行的同一位置肯定不为'1'.因为'1'代表竖放的上面那一格,下一个为零才行,不然就表示两个竖放的重叠了了一格,肯定不合法,我们对两个二进制串进行&运算,那么结果为1就是不合法状态.然后我们再想,' 1 '与' 1 '就算不对应,也有不合法的状态,例如上行的' 1 '就一定会占下一行的'0',在下一行一段的'0'被占后,若连续的'0'为奇数,则表示横放绝对不合法.如何表示?我们两个二进制串进行|运算,我们发现运算后的字符串中字符为'1'的情况为'0 1'或'1 0'(前面的为上,后面的为下)'0 1'则表示上面为横放的点(也可能为上一个竖放的下一个点),下面为竖放的上点显然对这一行的横放不影响.'1 0'则表示这点竖放,影响下一行,也对这一行的横放不影响.那剩下的为'0 0',表示上行横放,这一行也横放,那我们必须让连续的零为偶数才能合法匹配.

 

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#define e exit(0)
#define R register
#define ll long long
int main()
long long W,H,num,sum,f[13][2050],check[2050];
{
    freopen("floor.in","r",stdin);
    freopen("floor.out","w",stdout);
    scanf("%lld%lld",&W,&H);
    if((W&1)&&(H&1)){
        printf("0");
        return 0;
    }
    for(R int i=0;i<(1<<H);++i){
        num=sum=0;
        for(R int j=0;j<H;++j)
            if((1<<j)&i)
                num|=sum,sum=0;
            else sum^=1;
        check[i]=num|sum ? 0: 1;
    }
    f[0][0]=1;
    for(R ll i=1;i<=W;++i)
        for(R ll j=0;j<(1<<H);++j)
        {
            f[i][j]=0;
            for(R ll k=0;k<(1<<H);++k)
                if(!(j&k)&&check[j|k])
                    f[i][j]+=f[i-1][k];
        }
    printf("%lld",f[W][0]);
    return 0;
}

 

④一点技巧与细节:

　①:对于|运算后判断连续的零是否为偶数,我们可以预处理.

　②:可能最末尾有连续的零为奇数,没有'1'去停止它,用'1'停止记数时注意.

　③:对于语句if((1<<j)&i)是表示判断i的第j位是否为1,是一种常用技巧.