数据挖掘之决策树

决策树

1.决策树基本概念

决策树属于也只能非参数学习算法、可以用于解决(多)分类问题，回归问题。 回归问题的结果，叶子结点的平均值是回归问题的解。
根节点：决策树具有数据结构里面的二叉树、树的全部属性
非叶子节点 ：（决策点） 代表测试的条件，数据的属性的测试
叶子节点 ：分类后获得分类标记
分支： 测试的结果

2.信息熵

信息熵代表着一个数据的混乱程度，也称为不确定性。当数据集的信息熵越小，其不确定性因素越少，各个类别间界限越明确，可以衡量分类的效果。

2.1信息熵的计算

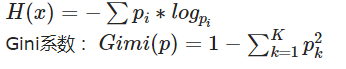
3.决策树的构建

如何选取分裂节点（根节点）：考虑每一个特征的信息增益，或者基尼系数增益，选取增益最大的为根节点。然后根据选取出的特征属性所具有的N个不同属性取值将数据集划分为N个集合。对这N个集合重复以上步骤，直到叶子结点则结束（这时候说明叶子结点对应的父节点在这个属性取值下都是同一个分类结果，此时熵为0，可以直接作出分类判断）。

4.信息增益(对应ID3算法)：

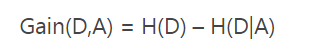
缺点：信息增益偏向取值较多的特征（原因：当特征的取值较多时，根据此特征划分更容易得到纯度更高的子集，因此划分后的熵更低，即不确定性更低，因此信息增益更大
具体特征所对应的信息增益计算：

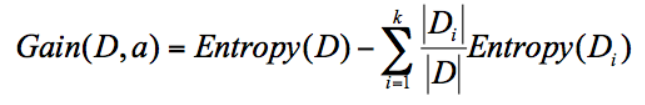
其中Di是由特征a的不同属性取值所分割的部分数据集，Entropy(Di)表示这部分数据集的经验熵,Entropy(D)是D数据集的经验熵

5.信息增益率(对应C4.5算法)

由于仅仅考虑信息增益，存在着缺点，比如Id，这是一个对于分类来说没有作用的属性，但由于Id是唯一的，当数据集由14个样本构成时，就有Id属性就有14个不同的取值，我们依据Id的不同属性取值划分为14个子集，每一个子集都只有一个样本，每一个子集都能唯一确定一个分类结果，不确定因素为0，这样算出来的信息增益最大，但对分类毫无作用。因为在给出测试样本时，Id是不可能出现在训练集中的，此时根本无法判断。因此考虑一个信息增益率，信息增益率具体计算如下:
信息增益率=信息增益/属性熵(即在该特征下的熵)
属性熵具体计算，是以该特征属性取值为随机变量，计算对应的熵值。当用频率表示概率时，统计该特征属性不同取值出现的次数，而不是统计样本的分类结果。
采用信息增益率表示时，就算出现信息增益很大的情况，由于还要考虑属性熵，则避免了上面的Id例子的情况。

以上的信息增益和信息增益率都只适合用来做分类任务

6.CART（分类树、回归树）

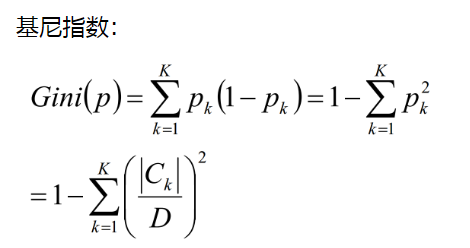
6.1 回归树

我们上面讨论的都是将决策树用于分类任务，也就是说，判断结果是离散的标签值，而我们知道，预测任务还有回归问题，决策树也可用于回归任务，即对连续值的预测，例如房价预测问题。那么如何用决策树来解决回归问题呢。

6.1.1 回归树的两个核心问题

（1）如何选择切分点 （2）如何判定输出值
切分点：最小二乘法 输出值：输出单元的均值
决策树回归问题举例