bzoj 1001 狼抓兔子

题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=1001

题解：

　　其实刚布置这道题的时候，我是拒绝的，后来听大犇们的的话，潜下心来学了一点（又经过数小时的调试之后）才写出了正解

　　正解的概念表达是：利用平面图的性质，把最大流问题转化成最小割问题，再用最短路来解决（其实我也不懂这TM都是什么鬼）

先介绍一下对偶图吧：

　　对于每一个平面图G，都有一个对偶图G'与之对应，其构造方法如下：
　　图G一个面为图G'中的一个点，图G中一条边的割线为图G'这条边两边两个面（所对应的点）之间的连线，边权也相等

　　如果一条边只处于一个面内，就构造那个面自己连向自己的边（这条性质在这道题中并没有用到）

对偶图构造样例（来自@Reddest）：

平面图G：

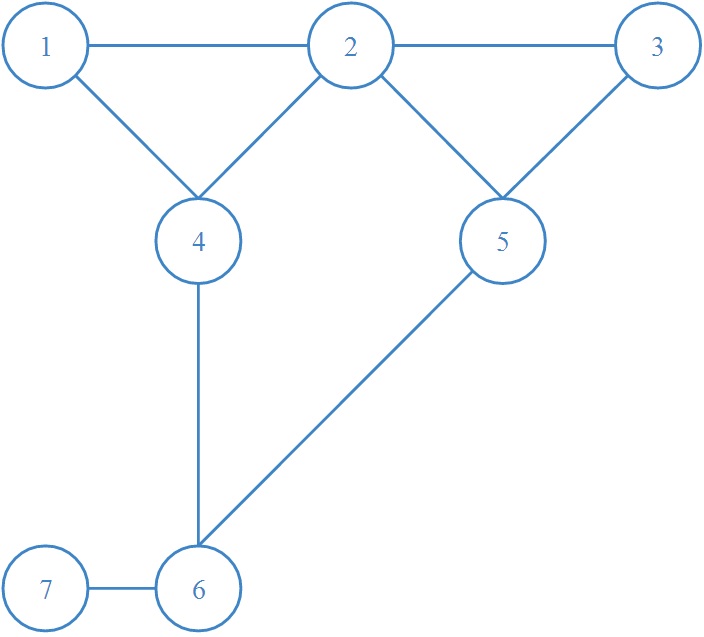
对偶图G'：

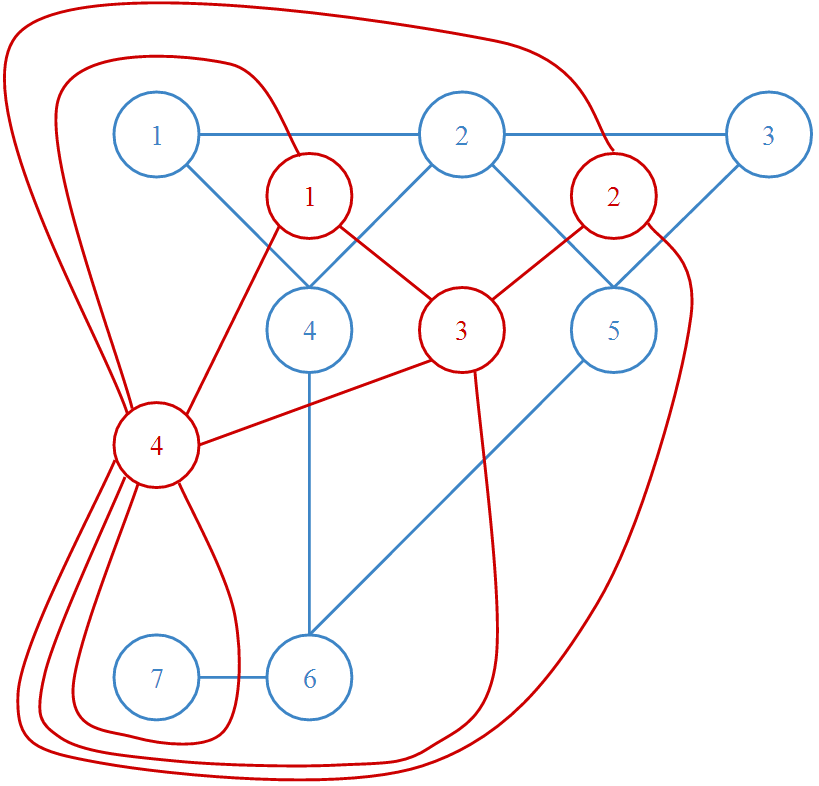
得到平面图与对偶图之间的关系：对偶图的点数等于平面图的面数，对偶图的边数等于平面图的边数

（更多证明以及性质定理之类的参见：http://wenku.baidu.com/link?url=RrUA5Y4dLzHhv_rO0UvuXeNnuOiGCryuYqQSRiBMurEevkJZ_kJcNueWMtqFTz7kZDbLFzVufYQNr_invfHnZnmIXTNED1W0rJ_Qab9YYhW）

　　那么，对于这道题来说还要再加几步：在构造对偶图之前在起点和终点之间连一条边，把最外层的面分成两半，一个作为起点，一个作为终点；

　　构造过程中，不要构造起点和终点之间的边（其实虚拟出来的边没有边权，也没法构造）

构造样例的对偶图：

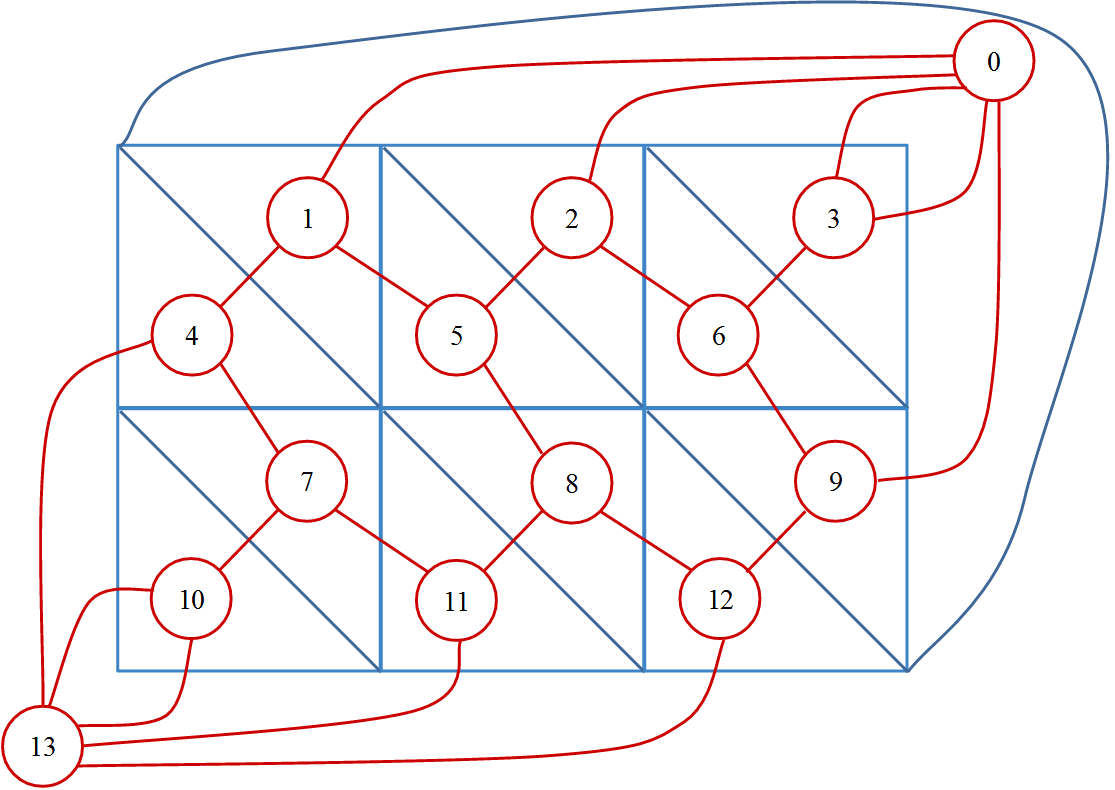
接着用各种算法求最短路即可

我用的SPFA：

#include<cstdio>
#define MAXN 2000000
#define INF 214748364
int n,m,nn,heads[MAXN],d[MAXN],q[MAXN],head,tail,cnt;
bool viss[MAXN];
struct edge
{
    int v,next,val;
}e[MAXN*3];
inline int min(int x,int y)
{
    return x<y?x:y;
}
void add(int x,int y,int z)
{
    e[++cnt]=(edge){y,heads[x],z};
    heads[x]=cnt;
}
void inedge()//建对偶图 
{
    int x,cnt;
    //横边 
    for(int i=1;i<=m-1;i++)
    {
        scanf("%d",&x);
        add(0,i,x);add(i,0,x);
    }
    cnt=(m-1)*2;
    for(int i=2;i<n;i++)
    {
        for(int j=1;j<=m-1;j++)
        {
            cnt++;
            scanf("%d",&x);
            add(cnt,cnt-m+1,x);add(cnt-m+1,cnt,x);
        }
        cnt+=(m-1);
    }
    for(int i=1;i<=m-1;i++)
    {
        scanf("%d",&x);
        add(nn,nn-m+i,x);add(nn-m+i,nn,x);
    }
    //竖边 
    cnt=m;
    for(int i=1;i<=n-1;i++)
    {
        scanf("%d",&x);
        add(cnt,nn,x);add(nn,cnt,x);
        for(int j=2;j<m;j++)
        {
            cnt++;
            scanf("%d",&x);
            add(cnt,cnt-m,x);add(cnt-m,cnt,x);
        }
        scanf("%d",&x);
        add(0,cnt-m+1,x);add(cnt-m+1,0,x);
        cnt+=m;
    }
    //斜边 
    cnt=0;
    for(int i=1;i<=n-1;i++)
    {
        for(int j=1;j<=m-1;j++)
        {
            cnt++;
            scanf("%d",&x);
            add(cnt,cnt+m-1,x);add(cnt+m-1,cnt,x);
        }
        cnt+=(m-1);
    }
}
void SPFA()
{
    head=1;tail=2;
    q[1]=0;
    viss[0]=true;
    while(head<tail)
    {
        for(int i=heads[q[head]];i;i=e[i].next)
        {
            if(d[q[head]]+e[i].val<d[e[i].v])
            {
                d[e[i].v]=d[q[head]]+e[i].val;
                if(!viss[e[i].v])
                {
                    q[tail++]=e[i].v;
                    viss[e[i].v]=true;
                }
            }
        }
        viss[q[head++]]=false;
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    if(n==1)//特判
    {
        int x,ans=INF;
        for(int i=1;i<=m-1;i++)
        {
            scanf("%d",&x);
            ans=min(ans,x);
        }
        printf("%d\n",ans==INF?0:ans);
        return 0;
    }
    else if(m==1)
    {
        int x,ans=INF;
        for(int i=1;i<=n-1;i++)
        {
            scanf("%d",&x);
            ans=min(ans,x);
        }
        printf("%d\n",ans==INF?0:ans);
        return 0;
    }
    nn=(n-1)*(m-1)*2+1;
    inedge();
    for(int i=1;i<=nn;i++)d[i]=INF;
    SPFA();
    printf("%d\n",d[nn]);
    return 0;
}