图论-二分图匹配-匈牙利算法
有关概念：
二分图：图G中的点集可以分为两个互不相交的子集，且G中的每条边连接的两个点分别属于这两个子集
二分图匹配：二分图G的子图M中每个结点上只连一条边，则称M为一个匹配
极大匹配：无法再向二分图中加边且满足匹配条件的匹配
最大匹配：所有极大匹配中边数最多的一个
增广路：若P为图G上连接两个未匹配结点的路径，且已匹配边和未匹配边在P上交替出现，则称P为相对于M的一条增广路
匈牙利算法即用来求二分图的极大匹配
思路：
在图G中找出增广路P，对P上每一条边取反（即已匹配边改为未匹配边，未匹配边改为已匹配边），重复直到找不到增广路为止
样例推导：
给出一幅二分图
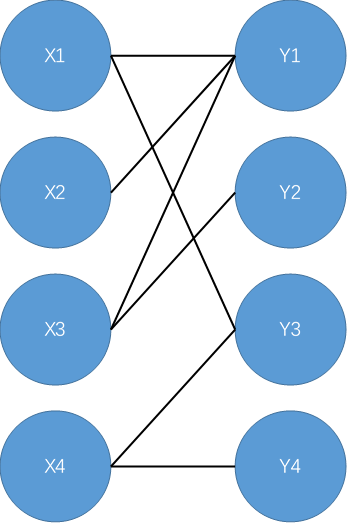
从X1开始，搜到X1-Y1，成增广路，连接X1-Y1
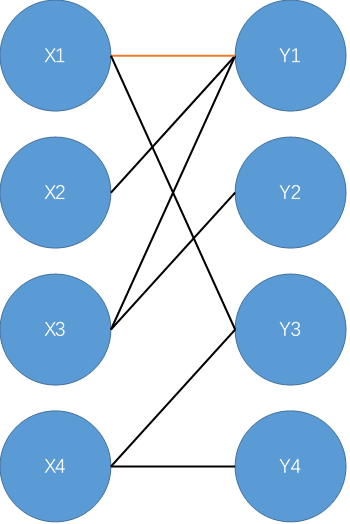
[ATTENTION]从X2开始，搜到X2-Y1-X1-Y3，成增广路
[ATTENTION] 取消连接X1-Y1，连接X1-Y3，X2-Y1
从X3开始，搜到X3-Y1-X2，不通，不作更改
搜到X3-Y2，成增广路，连接X3-Y2
从X4开始，搜到X4-Y3-X1-Y1-X2，不通，不作更改
搜到X4-Y4，成增广路，连接X4-Y4
至此找出极大增广路
邻接表
1 #include<cstdio> 2 #include<cstring> 3 #define MAXN 4 int n,m,cnt,match[MAXN],head[MAXN],ans; 5 bool check[MAXN]; 6 struct node 7 { 8 int v,next; 9 }edge[MAXN*5]; 10 void add(int x,int y) 11 { 12 edge[++cnt].next=head[x]; 13 head[x]=cnt; 14 edge[cnt].v=y; 15 } 16 bool Hungary(int u) 17 { 18 for(int i=head[u];i;i=edge[i].next) 19 { 20 int v=edge[i].v; 21 if(!check[v])//判断v是否在增广路中 22 { 23 check[v]=true; 24 if(!match[v]||Hungary(match[v])) 25 { 26 match[v]=u;//v对应u 27 return true; 28 } 29 } 30 } 31 return false; 32 } 33 int main() 34 { 35 //省略输入 36 for(int i=1;i<=n;i++) 37 { 38 if(!match[i]) 39 { 40 memset(check,false,sizeof(check)); 41 if(Hungary(i))ans++; 42 } 43 } 44 printf("%d\n",ans); 45 return 0; 46 }
邻接矩阵
1 #include<cstdio> 2 #include<cstring> 3 #define MAXN 4 int n,m,cnt,match[MAXN],map[MAXN][MAXN],ans; 5 bool check[MAXN]; 6 bool Hungary(int u) 7 { 8 for(int i=1;i<=n;i++) 9 { 10 if(!check[i]&&map[u][i]) 11 { 12 check[i]=true; 13 if(!match[i]||Hungary(match[i])) 14 { 15 match[i]=u; 16 return true; 17 } 18 } 19 } 20 return false; 21 } 22 int main() 23 { 24 //省略输入 25 for(int i=1;i<=n;i++) 26 { 27 if(!match[i]) 28 { 29 memset(check,false,sizeof(check)); 30 if(Hungary(i))ans++; 31 } 32 } 33 printf("%d\n",ans); 34 return 0; 35 }
*参考：https://www.byvoid.com/blog/hungary/
