MD5摘要算法简析
1 MD5简介
1.1 概述
MD5即Message-Digest Algorithm 5（信息-摘要算法5），用于确保信息传输完整一致。是计算机广泛使用的杂凑算法之一（又译摘要算法、哈希算法），主流编程语言普遍已有MD5实现。将数据（如汉字）运算为另一固定长度值，是杂凑算法的基础原理，MD5的前身有MD2、MD3和MD4。
1.2 发展历史
MD2
Rivest在1989年开发出MD2算法。在这个算法中，首先对信息进行数据补位，使信息的字节长度是16的倍数。然后，以一个16位的检验和追加到信息末尾，并且根据这个新产生的信息计算出散列值。后来，Rogier和Chauvaud发现如果忽略了检验将和MD2产生冲突。MD2算法加密后结果是唯一的（即不同信息加密后的结果不同）。
MD4
为了加强算法的安全性，Rivest在1990年又开发出MD4算法。MD4算法同样需要填补信息以确保信息的比特位长度减去448后能被512整除（信息比特位长度mod 512 = 448）。然后，一个以64位二进制表示的信息的最初长度被添加进来。信息被处理成512位damg?rd/merkle迭代结构的区块，而且每个区块要通过三个不同步骤的处理。Den boer和Bosselaers以及其他人很快的发现了攻击MD4版本中第一步和第三步的漏洞。Dobbertin向大家演示了如何利用一部普通的个人电脑在几分钟内找到MD4完整版本中的冲突（这个冲突实际上是一种漏洞，它将导致对不同的内容进行加密却可能得到相同的加密后结果）。毫无疑问，MD4就此被淘汰掉了。
尽管MD4算法在安全上有个这么大的漏洞，但它对在其后才被开发出来的好几种信息安全加密算法的出现却有着不可忽视的引导作用。
MD5
1991年，Rivest开发出技术上更为趋近成熟的md5算法。它在MD4的基础上增加了"安全-带子"（safety-belts）的概念。虽然MD5比MD4复杂度大一些，但却更为安全。这个算法很明显的由四个和MD4设计有少许不同的步骤组成。在MD5算法中，信息-摘要的大小和填充的必要条件与MD4完全相同。Den boer和Bosselaers曾发现MD5算法中的假冲突（pseudo-collisions），但除此之外就没有其他被发现的加密后结果了。
1.3 MD5算法原理
对于MD5算法可以简要的概括为：MD5是以512位分组来处理输入信息，且每一分组又被划分为16个32位子分组，经过了一系列的处理后，算法的输出由四个32位分组组成，将这四个32位分组级联后将生成一个128位散列值。
总体流程图如下：
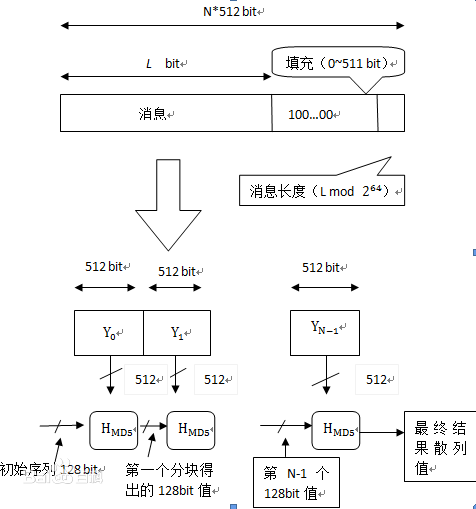
1.3.1 填充
在MD5算法中，首先需要对信息进行填充，使其位长对512求余的结果等于448，并且填充必须进行，即使其位长对512求余的结果等于448。因此，信息的位长（Bits Length）将被扩展至N*512+448，N为一个非负整数，N可以是零。
填充的方法如下：
1) 在信息的后面填充一个1和无数个0，直到满足上面的条件时才停止用0对信息的填充。
2) 在这个结果后面附加一个以64位二进制表示的填充前信息长度（单位为Bit），如果二进制表示的填充前信息长度超过64位，则取低64位。
经过这两步的处理，信息的位长=N*512+448+64=(N+1）*512，即长度恰好是512的整数倍。这样做的原因是为满足后面处理中对信息长度的要求。
1.3.2 初始化变量
初始的128位值为初试链接变量，这些参数用于第一轮的运算，以大端字节序来表示，他们分别为： A=0x01234567，B=0x89ABCDEF，C=0xFEDCBA98，D=0x76543210。
（每一个变量给出的数值是高字节存于内存低地址，低字节存于内存高地址，即大端字节序。在程序中变量A、B、C、D的值分别为0x67452301，0xEFCDAB89，0x98BADCFE，0x10325476）
1.3.3 处理分组数据
每一分组的算法流程如下：
第一分组需要将上面四个链接变量复制到另外四个变量中：A到a，B到b，C到c，D到d。从第二分组开始的变量为上一分组的运算结果，即A = a， B = b， C = c， D = d。
主循环有四轮（MD4只有三轮），每轮循环都很相似。第一轮进行16次操作。每次操作对a、b、c和d中的其中三个作一次非线性函数运算，然后将所得结果加上第四个变量，文本的一个子分组和一个常数。再将所得结果向左环移一个不定的数，并加上a、b、c或d中之一。最后用该结果取代a、b、c或d中之一。
以下是每次操作中用到的四个非线性函数（每轮一个）。
F( X ,Y ,Z ) = ( X & Y ) | ( (~X) & Z )
G( X ,Y ,Z ) = ( X & Z ) | ( Y & (~Z) )
H( X ,Y ,Z ) =X ^ Y ^ Z
I( X ,Y ,Z ) =Y ^ ( X | (~Z) )
（&是与（And），|是或（Or），~是非（Not），^是异或（Xor））
这四个函数的说明：如果X、Y和Z的对应位是独立和均匀的，那么结果的每一位也应是独立和均匀的。
F是一个逐位运算的函数。即，如果X，那么Y，否则Z。函数H是逐位奇偶操作符。
假设Mj表示消息的第j个子分组（从0到15），常数ti是4294967296*abs( sin(i) ）的整数部分，i 取值从1到64，单位是弧度。（4294967296=232）
现定义：
FF(a ,b ,c ,d ,Mj ,s ,ti ) 操作为 a = b + ( (a + F(b,c,d) + Mj + ti) << s)
GG(a ,b ,c ,d ,Mj ,s ,ti ) 操作为 a = b + ( (a + G(b,c,d) + Mj + ti) << s)
HH(a ,b ,c ,d ,Mj ,s ,ti) 操作为 a = b + ( (a + H(b,c,d) + Mj + ti) << s)
II(a ,b ,c ,d ,Mj ,s ,ti) 操作为 a = b + ( (a + I(b,c,d) + Mj + ti) << s)
注意：“<<”表示循环左移位，不是左移位。
这四轮（共64步）是：
第一轮
FF(a ,b ,c ,d ,M0 ,7 ,0xd76aa478 )
FF(d ,a ,b ,c ,M1 ,12 ,0xe8c7b756 )
FF(c ,d ,a ,b ,M2 ,17 ,0x242070db )
FF(b ,c ,d ,a ,M3 ,22 ,0xc1bdceee )
FF(a ,b ,c ,d ,M4 ,7 ,0xf57c0faf )
FF(d ,a ,b ,c ,M5 ,12 ,0x4787c62a )
FF(c ,d ,a ,b ,M6 ,17 ,0xa8304613 )
FF(b ,c ,d ,a ,M7 ,22 ,0xfd469501)
FF(a ,b ,c ,d ,M8 ,7 ,0x698098d8 )
FF(d ,a ,b ,c ,M9 ,12 ,0x8b44f7af )
FF(c ,d ,a ,b ,M10 ,17 ,0xffff5bb1 )
FF(b ,c ,d ,a ,M11 ,22 ,0x895cd7be )
FF(a ,b ,c ,d ,M12 ,7 ,0x6b901122 )
FF(d ,a ,b ,c ,M13 ,12 ,0xfd987193 )
FF(c ,d ,a ,b ,M14 ,17 ,0xa679438e )
FF(b ,c ,d ,a ,M15 ,22 ,0x49b40821 )
第二轮
GG(a ,b ,c ,d ,M1 ,5 ,0xf61e2562 )
GG(d ,a ,b ,c ,M6 ,9 ,0xc040b340 )
GG(c ,d ,a ,b ,M11 ,14 ,0x265e5a51 )
GG(b ,c ,d ,a ,M0 ,20 ,0xe9b6c7aa )
GG(a ,b ,c ,d ,M5 ,5 ,0xd62f105d )
GG(d ,a ,b ,c ,M10 ,9 ,0x02441453 )
GG(c ,d ,a ,b ,M15 ,14 ,0xd8a1e681 )
GG(b ,c ,d ,a ,M4 ,20 ,0xe7d3fbc8 )
GG(a ,b ,c ,d ,M9 ,5 ,0x21e1cde6 )
GG(d ,a ,b ,c ,M14 ,9 ,0xc33707d6 )
GG(c ,d ,a ,b ,M3 ,14 ,0xf4d50d87 )
GG(b ,c ,d ,a ,M8 ,20 ,0x455a14ed )
GG(a ,b ,c ,d ,M13 ,5 ,0xa9e3e905 )
GG(d ,a ,b ,c ,M2 ,9 ,0xfcefa3f8 )
GG(c ,d ,a ,b ,M7 ,14 ,0x676f02d9 )
GG(b ,c ,d ,a ,M12 ,20 ,0x8d2a4c8a )
第三轮
HH(a ,b ,c ,d ,M5 ,4 ,0xfffa3942 )
HH(d ,a ,b ,c ,M8 ,11 ,0x8771f681 )
HH(c ,d ,a ,b ,M11 ,16 ,0x6d9d6122 )
HH(b ,c ,d ,a ,M14 ,23 ,0xfde5380c )
HH(a ,b ,c ,d ,M1 ,4 ,0xa4beea44 )
HH(d ,a ,b ,c ,M4 ,11 ,0x4bdecfa9 )
HH(c ,d ,a ,b ,M7 ,16 ,0xf6bb4b60 )
HH(b ,c ,d ,a ,M10 ,23 ,0xbebfbc70 )
HH(a ,b ,c ,d ,M13 ,4 ,0x289b7ec6 )
HH(d ,a ,b ,c ,M0 ,11 ,0xeaa127fa )
HH(c ,d ,a ,b ,M3 ,16 ,0xd4ef3085 )
HH(b ,c ,d ,a ,M6 ,23 ,0x04881d05 )
HH(a ,b ,c ,d ,M9 ,4 ,0xd9d4d039 )
HH(d ,a ,b ,c ,M12 ,11 ,0xe6db99e5 )
HH(c ,d ,a ,b ,M15 ,16 ,0x1fa27cf8 )
HH(b ,c ,d ,a ,M2 ,23 ,0xc4ac5665 )
第四轮
II(a ,b ,c ,d ,M0 ,6 ,0xf4292244 )
II(d ,a ,b ,c ,M7 ,10 ,0x432aff97 )
II(c ,d ,a ,b ,M14 ,15 ,0xab9423a7 )
II(b ,c ,d ,a ,M5 ,21 ,0xfc93a039 )
II(a ,b ,c ,d ,M12 ,6 ,0x655b59c3 )
II(d ,a ,b ,c ,M3 ,10 ,0x8f0ccc92 )
II(c ,d ,a ,b ,M10 ,15 ,0xffeff47d )
II(b ,c ,d ,a ,M1 ,21 ,0x85845dd1 )
II(a ,b ,c ,d ,M8 ,6 ,0x6fa87e4f )
II(d ,a ,b ,c ,M15 ,10 ,0xfe2ce6e0 )
II(c ,d ,a ,b ,M6 ,15 ,0xa3014314 )
II(b ,c ,d ,a ,M13 ,21 ,0x4e0811a1 )
II(a ,b ,c ,d ,M4 ,6 ,0xf7537e82 )
II(d ,a ,b ,c ,M11 ,10 ,0xbd3af235 )
II(c ,d ,a ,b ,M2 ,15 ,0x2ad7d2bb )
II(b ,c ,d ,a ,M9 ,21 ,0xeb86d391 )
所有这些完成之后，将a、b、c、d分别在原来基础上再加上A、B、C、D。
即a = a + A，b = b + B，c = c + C，d = d + D
然后用下一分组数据继续运行以上算法。
1.3.4 输出
最后的输出是a、b、c和d的级联。
当你按照我上面所说的方法实现MD5算法以后，你可以用以下几个信息对你做出来的程序作一个简单的测试，看看程序有没有错误。
MD5 ("") = d41d8cd98f00b204e9800998ecf8427e
MD5 ("a") = 0cc175b9c0f1b6a831c399e269772661
MD5 ("abc") = 900150983cd24fb0d6963f7d28e17f72
MD5 ("message digest") = f96b697d7cb7938d525a2f31aaf161d0
MD5 ("abcdefghijklmnopqrstuvwxyz") = c3fcd3d76192e4007dfb496cca67e13b
MD5 ("ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz") =f29939a25efabaef3b87e2cbfe641315
MD5 ("8a683566bcc7801226b3d8b0cf35fd97") =cf2cb5c89c5e5eeebef4a76becddfcfd
1.4 MD5应用
1.4.1 一致性验证
MD5的典型应用是对一段信息（Message）产生信息摘要（Message-Digest），以防止被篡改。比如，在Unix下有很多软件在下载的时候都有一个文件名相同，文件扩展名为.md5的文件，在这个文件中通常只有一行文本，大致结构如：
MD5 (tanajiya.tar.gz) = 38b8c2c1093dd0fec383a9d9ac940515
这就是tanajiya.tar.gz文件的数字签名。MD5将整个文件当作一个大文本信息，通过其不可逆的字符串变换算法，产生了这个唯一的MD5信息摘要。为了让读者朋友对MD5的应用有个直观的认识，笔者以一个比方和一个实例来简要描述一下其工作过程：
大家都知道，地球上任何人都有自己独一无二的指纹，这常常成为司法机关鉴别罪犯身份最值得信赖的方法；与之类似，MD5就可以为任何文件（不管其大小、格式、数量）产生一个同样独一无二的“数字指纹”，如果任何人对文件做了任何改动，其MD5值也就是对应的“数字指纹”都会发生变化。
我们常常在某些软件下载站点的某软件信息中看到其MD5值，它的作用就在于我们可以在下载该软件后，对下载回来的文件用专门的软件（如Windows MD5 Check等）做一次MD5校验，以确保我们获得的文件与该站点提供的文件为同一文件。
具体来说文件的MD5值就像是这个文件的“数字指纹”。每个文件的MD5值是不同的，如果任何人对文件做了任何改动，其MD5值也就是对应的“数字指纹”就会发生变化。比如下载服务器针对一个文件预先提供一个MD5值，用户下载完该文件后，用我这个算法重新计算下载文件的MD5值，通过比较这两个值是否相同，就能判断下载的文件是否出错，或者说下载的文件是否被篡改了。
利用MD5算法来进行文件校验的方案被大量应用到软件下载站、论坛数据库、系统文件安全等方面。
1.4.2 数字签名
MD5的典型应用是对一段Message(字节串)产生fingerprint(指纹），以防止被“篡改”。举个例子，你将一段话写在一个叫 readme.txt文件中，并对这个readme.txt产生一个MD5的值并记录在案，然后你可以传播这个文件给别人，别人如果修改了文件中的任何内容，你对这个文件重新计算MD5时就会发现（两个MD5值不相同）。如果再有一个第三方的认证机构，用MD5还可以防止文件作者的“抵赖”，这就是所谓的数字签名应用。
1.4.3 安全访问认证
MD5还广泛用于操作系统的登陆认证上，如Unix、各类BSD系统登录密码、数字签名等诸多方面。如在Unix系统中用户的密码是以MD5（或其它类似的算法）经Hash运算后存储在文件系统中。当用户登录的时候，系统把用户输入的密码进行MD5 Hash运算，然后再去和保存在文件系统中的MD5值进行比较，进而确定输入的密码是否正确。通过这样的步骤，系统在并不知道用户密码的明码的情况下就可以确定用户登录系统的合法性。这可以避免用户的密码被具有系统管理员权限的用户知道。MD5将任意长度的“字节串”映射为一个128bit的大整数，并且是通过该128bit反推原始字符串是困难的，换句话说就是，即使你看到源程序和算法描述，也无法将一个MD5的值变换回原始的字符串，从数学原理上说，是因为原始的字符串有无穷多个，这有点象不存在反函数的数学函数。所以，要遇到了md5密码的问题，比较好的办法是：你可以用这个系统中的md5（）函数重新设一个密码，如admin，把生成的一串密码的Hash值覆盖原来的Hash值就行了。
1.5 MD5特点
MD5算法具有以下特点：
1、压缩性：任意长度的数据，算出的MD5值长度都是固定的。
2、容易计算：从原数据计算出MD5值很容易。
3、抗修改性：对原数据进行任何改动，哪怕只修改1个字节，所得到的MD5值都有很大区别。
4、强抗碰撞：已知原数据和其MD5值，想找到一个具有相同MD5值的数据（即伪造数据）是非常困难的。
MD5的作用是让大容量信息在用数字签名软件签署私人密钥前被"压缩"成一种保密的格式（就是把一个任意长度的字节串变换成一定长的十六进制数字串）。除了MD5以外，其中比较有名的还有sha-1、RIPEMD以及Haval等。
2 java代码实现MD5摘要算法
2.1 MD5详细实现代码
1 package xin.dreaming.md5; 2 3 public class MD5 { 4 /* 5 *四个链接变量 6 */ 7 private final int A=0x67452301; 8 private final int B=0xefcdab89; 9 private final int C=0x98badcfe; 10 private final int D=0x10325476; 11 /* 12 *ABCD的临时变量 13 */ 14 private int Atemp,Btemp,Ctemp,Dtemp; 15 16 /* 17 *常量ti 18 *公式:floor(abs(sin(i+1))×(2pow32) 19 */ 20 private final int K[]={ 21 0xd76aa478,0xe8c7b756,0x242070db,0xc1bdceee, 22 0xf57c0faf,0x4787c62a,0xa8304613,0xfd469501,0x698098d8, 23 0x8b44f7af,0xffff5bb1,0x895cd7be,0x6b901122,0xfd987193, 24 0xa679438e,0x49b40821,0xf61e2562,0xc040b340,0x265e5a51, 25 0xe9b6c7aa,0xd62f105d,0x02441453,0xd8a1e681,0xe7d3fbc8, 26 0x21e1cde6,0xc33707d6,0xf4d50d87,0x455a14ed,0xa9e3e905, 27 0xfcefa3f8,0x676f02d9,0x8d2a4c8a,0xfffa3942,0x8771f681, 28 0x6d9d6122,0xfde5380c,0xa4beea44,0x4bdecfa9,0xf6bb4b60, 29 0xbebfbc70,0x289b7ec6,0xeaa127fa,0xd4ef3085,0x04881d05, 30 0xd9d4d039,0xe6db99e5,0x1fa27cf8,0xc4ac5665,0xf4292244, 31 0x432aff97,0xab9423a7,0xfc93a039,0x655b59c3,0x8f0ccc92, 32 0xffeff47d,0x85845dd1,0x6fa87e4f,0xfe2ce6e0,0xa3014314, 33 0x4e0811a1,0xf7537e82,0xbd3af235,0x2ad7d2bb,0xeb86d391}; 34 /* 35 *向左位移数,计算方法未知 36 */ 37 private final int s[]={7,12,17,22,7,12,17,22,7,12,17,22,7, 38 12,17,22,5,9,14,20,5,9,14,20,5,9,14,20,5,9,14,20, 39 4,11,16,23,4,11,16,23,4,11,16,23,4,11,16,23,6,10, 40 15,21,6,10,15,21,6,10,15,21,6,10,15,21}; 41 42 43 /* 44 *初始化函数 45 */ 46 private void init(){ 47 Atemp=A; 48 Btemp=B; 49 Ctemp=C; 50 Dtemp=D; 51 } 52 /* 53 *移动一定位数 54 */ 55 private int shift(int a,int s){ 56 return(a<<s)|(a>>>(32-s));//右移的时候，高位一定要补零，而不是补充符号位 57 } 58 /* 59 *主循环 60 */ 61 private void MainLoop(int M[]){ 62 int F,g; 63 int a=Atemp; 64 int b=Btemp; 65 int c=Ctemp; 66 int d=Dtemp; 67 for(int i = 0; i < 64; i ++){ 68 if(i<16){ 69 F=(b&c)|((~b)&d); 70 g=i; 71 }else if(i<32){ 72 F=(d&b)|((~d)&c); 73 g=(5*i+1)%16; 74 }else if(i<48){ 75 F=b^c^d; 76 g=(3*i+5)%16; 77 }else{ 78 F=c^(b|(~d)); 79 g=(7*i)%16; 80 } 81 int tmp=d; 82 d=c; 83 c=b; 84 b=b+shift(a+F+K[i]+M[g],s[i]); 85 a=tmp; 86 } 87 Atemp=a+Atemp; 88 Btemp=b+Btemp; 89 Ctemp=c+Ctemp; 90 Dtemp=d+Dtemp; 91 92 } 93 /* 94 *填充函数 95 *处理后应满足bits≡448(mod512),字节就是bytes≡56（mode64) 96 *填充方式为先加一个0,其它位补零 97 *最后加上64位的原来长度 98 */ 99 private int[] add(String str){ 100 int num=((str.length()+8)/64)+1;//以512位，64个字节为一组 101 int strByte[]=new int[num*16];//64/4=16，所以有16个整数 102 for(int i=0;i<num*16;i++){//全部初始化0 103 strByte[i]=0; 104 } 105 int i; 106 for(i=0;i<str.length();i++){ 107 strByte[i>>2]|=str.charAt(i)<<((i%4)*8);//一个整数存储四个字节，小端序 108 } 109 strByte[i>>2]|=0x80<<((i%4)*8);//尾部添加1 110 /* 111 *添加原长度，长度指位的长度，所以要乘8，然后是小端序，所以放在倒数第二个,这里长度只用了32位 112 */ 113 strByte[num*16-2]=str.length()*8; 114 return strByte; 115 } 116 /* 117 *调用函数 118 */ 119 public String getMD5(String source){ 120 init(); 121 int strByte[]=add(source); 122 for(int i=0;i<strByte.length/16;i++){ 123 int num[]=new int[16]; 124 for(int j=0;j<16;j++){ 125 num[j]=strByte[i*16+j]; 126 } 127 MainLoop(num); 128 } 129 return changeHex(Atemp)+changeHex(Btemp)+changeHex(Ctemp)+changeHex(Dtemp); 130 131 } 132 /* 133 *整数变成16进制字符串 134 */ 135 private String changeHex(int a){ 136 String str=""; 137 for(int i=0;i<4;i++){ 138 str+=String.format("%2s", Integer.toHexString(((a>>i*8)%(1<<8))&0xff)).replace(' ', '0'); 139 140 } 141 return str; 142 } 143 /* 144 *单例 145 */ 146 private static MD5 instance; 147 public static MD5 getInstance(){ 148 if(instance==null){ 149 instance=new MD5(); 150 } 151 return instance; 152 } 153 154 private MD5(){}; 155 156 public static void main(String[] args){ 157 String str=MD5.getInstance().getMD5("123"); 158 System.out.println(str); 159 } 160 }
代码摘要结果：
此处代码可以参考前边MD5原理流程，了解其代码执行流程。
2.2 使用java.security.MessageDigest实现MD5摘要算法
2.2.1代码实现：
1 /** 2 * md5计算. 3 * 4 * @param datas 5 * 待计算的数据 6 * @return 计算结果 7 */ 8 public static byte[] md5(byte[] datas) { 9 MessageDigest md = null; 10 try { 11 md = MessageDigest.getInstance("MD5"); 12 md.reset(); 13 md.update(datas); 14 return md.digest(); 15 } catch (Exception e) { 16 LogUtil.writeErrorLog("MD5计算失败", e); 17 return null; 18 } 19 }
2.2.2 MessageDigest 简要说明
java.security.MessageDigest类用于为应用程序提供信息摘要算法的功能，如 MD5 或 SHA 算法。简单点说就是用于生成散列码。信息摘要是安全的单向哈希函数，它接收任意大小的数据，输出固定长度的哈希值。关于信息摘要和散列码请参照《数字证书简介》
MessageDigest 通过其getInstance系列静态函数来进行实例化和初始化。MessageDigest 对象通过使用 update 方法处理数据。任何时候都可以调用 reset 方法重置摘要。一旦所有需要更新的数据都已经被更新了，应该调用 digest 方法之一完成哈希计算并返回结果。
对于给定数量的更新数据，digest 方法只能被调用一次。digest 方法被调用后，MessageDigest 对象被重新设置成其初始状态。
MessageDigest 的实现可随意选择是否实现 Cloneable 接口。客户端应用程可以通过尝试复制和捕获 CloneNotSupportedException 测试可复制性：
参考：
1、https://baike.baidu.com/item/MD5/212708?fr=aladdin#1_3
2、http://hubingforever.blog.163.com/blog/static/171040579201210781650340/
追梦若冷 就用希望去暖
