《编译原理》构造与正规式 (0|1)*01 等价的 DFA - 例题解析
《编译原理》构造与正规式 (0|1)*01 等价的 DFA - 例题解析
解题步骤：
- NFA 状态转换图
- 子集法
- DFA 的状态转换矩阵
- DFA 的状态转图
解：
已给正规式：(0|1)*01
画出 NFA 状态转换图如下：
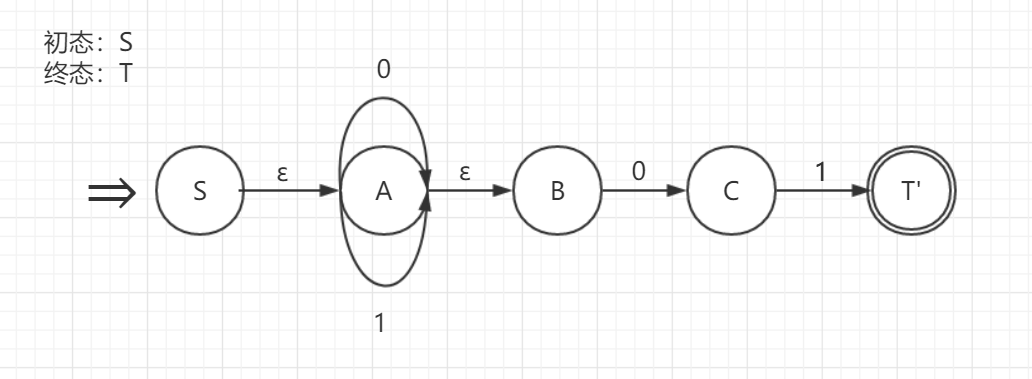
子集法的表格：
| I状态\字符 | I0 | I1 |
|---|---|---|
| {S, A, B} 求法： 表示开始符号，以及开始符号识别 n 个 ε 可以到达的状态集合。如本题中： 开始符号 S，通过识别 ε 可以到达的转态有 A, B，所以集合为 | {A, B, C} 求法： 表示改行最左端的状态集，识别最上端的符号可以到达的状态，以及这些状态识别 n 个 ε 可以到达的状态的集合。如本题中： 有 {S, A, B}，逐个判断 S 识别 0 弧没有可以到达的状态；A 识别 0 可以到达 A，B 识别 0 可以到达 C；现在已有 A, C 状态，又因为 A 状态识别 ε 可以到达 B，所以整个集合为 | {A, B} 求法： 同相邻左测表格求法。如本题中： 有 {S, A, B}，S 状态识别 1 没有可以到达的状态，A 识别 1 可以到达 A，B 识别 1 没有可以到达的状态。所以此时只有 A。又因为 A 状态识别 ε 可以到达 B，所以整个集合为 |
| {A, B, C} 求法： 这个为什么是 {A, B, C}？因为 相邻右上方表格为 {A, B, C} 为什么用相邻右上方表格的状态集？因为 它是初始态，仅识别 0 和 ε 就能到达的状态集。所以，可以将该状态集视为识别一条弧所到达的状态集。可以看做是下一状态，为起状态别名做准备。 | {A, B, C} 注： 有 A 就有 B | |
对状态中间重命名，求新的状态转换矩阵：
（1）因为 S 是初态，重命名为 S'，也是终态
（2）设 {A, B, C} 为 A'
（3）设 {A, B} 为 B'
（4）因为 T 是终态，此时 {A, B, T} 不是相当于 A' 识别 1 弧所到达的状态，T 是终态，{A, B, T} 也是终态，重命名为 T'
| I状态\字符 | I0 | I1 |
|---|---|---|
| S' | A' | B' |
| A' | A' | T' |
| B' | A' | B' |
| T' | A' | B' |
画出 NFA 状态转换图如下：
验证
(0|1)*01 正规式对应的正规集元素特点是：
- 以 0 或 1 的任意组合，任意数量为开头
- 以 01 为结尾
当结尾为终结符时，可认为识别成功
