《编译原理》-用例题理解-自顶向下语法分析及 FIRST,FOLLOW,SELECT集,LL(1)文法
《编译原理》-用例题理解-自顶向下语法分析及 FIRST,FOLLOW,SELECT集,LL(1)文法
此编译原理确定某高级程序设计语言编译原理,理论基础,学习笔记
本笔记是对教材《编译原理》- 张晶老师版 做学习笔记。
最近在学《编译原理》,前三章感觉还可以理解,到了第四章就感觉这难度就上来了。就是说过了词法分析,刚到语法分析,就开始头大了,于是想做个笔记,本篇就是第 4 章的笔记。
(一)前言
第4章 - 自顶向下的语法分析
语法分析
语法分析是在词法分析识别出的单词符号串的基础上,分析并判定句子的语法结构是否符合语法规则
自顶向下分析法
自顶向下分析法就是从文法的开始符号出发,不断建立直接推导,试图构造一个最左推导序列,最终由它推导出与输入符号串完全匹配(相同)的句子。
从语法树的角度看,自顶向下分析法就是以开始符号为根节点,试图向下构造一棵语法树,其端末结符号串与输入符号串相同。
问题1:左递归问题
若采用自顶向下的语法分析,应消除文法中存在的左递归。
因为左递归的存在,有可能使推导不能结束,分析陷入循环状态。
例如:A → Aa | b
左递归还比较好理解,例如:我需要匹配的字符串是 bsd 就需要从左端 b 开始是被,推导时,先用 A -> Aa 推导 AAa,此时不符合条件,但因为还有非终结符,不能结束,而是继续推导。此时就会陷入死循环。
所以要避免这类情况就要消除左递归。
消除文法的左递归
课本上直接左递归,间接左递归,提取左公因子书上比较详细,一般可以理解,跳过了
问题2:回溯问题
因为推导时,右侧有或的情况,从各种可能的选择中随机挑选一种,并希望它是正确的。如果以后发现它是错误的,必须退回去,再试另外的选择这种方式称为回溯。
回溯代价极高,效率很低,所以也要避免。
所以需要FIRST 集,FOLLOW 集和 SELECT 集,这一堆集出马了。
(二)关于 FIRST 集 - 首终结符集
如果一个文法的每个产生式的右部都由终结符开始,有相同左部的产生式,它们的右部由不同的终结符开始,这样的文法在推导过程中就可以根据当前的输入符号来决定选择哪个产生式往下推导,它的分析过程是唯一确定的,不会产生回溯现象
简单的说,右部都以非终结符开头,每个产生式的右部第一个非终结符又都不一样就更好了,我们就可以根据语法唯一的选择产生式,
例如:需要识别输入符号串 bsd
文法:
(1)S -> aBC
(2)B -> cC
(3)C -> bB
(4)C -> d
......
我们知道 b 就可以选择 (3)
但是一般文法并不满足上述格式,例如:
S -> Af | Be
此时,还想使用相同方法,我们可以通过确定 Af 和 Be 推到最后的首终结符集(FIRST 集)来确定。
FIRST 集的定义
简单的说 FIRST 集就是一个文法符号串的开始符号集合
设 G=(VT,VN,S,P)是上下文无关文法,
FIRST(α)={a|α=>aβ,a∈VT,α,β∈v*}
若 α=> ε(经过0或多步推导可以推出为空串),则规定 ε ∈ FIRST(α)
FIRST(α) 是 α 的所有可能推导的开头终结符或可能的 ε。
例题 4.3:求 FIRST 集
题目:
给定文法 G[S]:
(1)S -> Af
(2)S -> Be
(3)A -> a
(4)A -> cA
(5)B -> b
(6)B -> dB
详解:
求(1)中的 Af 的 FIRST 集,注意,因为如果推出为空时用 ε,所以 A 后面的 f 是没用的,我们只分析 A 的第一个终结符的集。
因为(3)和(4)都是由 A 推导,所以两个都考虑
FIRST(Af) = FIRST(a) ∪ FIRST(cA) = {a,c}
同理可求出:
FIRST(Be)
FIRST(a)
FIRST(cA)
FIRST(dB)
(三)关于 FOLLOW 集 - 后随集
如果仅适用 FIRST 只能根据首字符不同选择产生式,如果首字符不同...
FOLLOW 集的定义
简单的说 FOLLOW 集就是一个文法符号的后跟终结符号的集合。
设 G =(VT,VN,S,P)是上下文无关文法,A∈VN,S是开始符号。
FOLLOW(A)={a|S=>*…Aa…,a ∈VT}
若有 S=>*…A(就是说 A 已经是最后一个时,没有后面的),则规定 # ∈ FOLLOW(A)
FOLLOW(A) 是所有出现在紧接 A 之后的终结符或 “#”;
FOLLOW 计算规则
(1) 对于文法的开始符号 S,置 # 到 FOLLOW(S) 中;
(2)若 A -> αBaβ 是一个产生式,a 为终结符,则把 a 加至 FOLLOW(B) 中;
(3)若 A -> αBβ 是一个产生式,则把 FIRST(β) - {ε} 加至 FOLLOW(B) 中;
(4)若 A -> αB 是一个产生式,或 A -> αBβ 是一个产生式,而 β =*> ε,
则把 FOLLOW(A) 加至 FOLLOW(B) 中
提示:
(1)就是说如果对开始符号求 FOLLOW(S) ,直接来个 # ∈FOLLOW(S) ,不过要表示成 {#}
(2)就是把后面的紧跟的终结符,就直接加到 FOLLOW 集
(3)正经的求 B 的 FOLLOW 集,就是 B 后面 β 的 FIRST(β) - {ε}
(4)分情况:
- 如果 A -> αB,就把 FOLLOW(A) 加至 FOLLOW(B) 中
- A -> αBβ 是一个产生式,此时 β 可以推成 ε,就是相当于也能推出 A -> αB,也把 FOLLOW(A) 加至 FOLLOW(B) 中
注意: (4)中这里是 FOLLOW(A) 加至 FOLLOW(B) ,就是左部的 FOLLOW 集,加到其推导出的右部的最后一个非终结符的 FOLLOW 集,
例如:需要识别输入符号串 :bsAcD,求 FOLLOW(B) 的时候
此时 FOLLOW(A) 就含有 c,如果 A -> dB,即此时 FOLLOW(B) 也应该有 c
记忆方式:
提示:这是规则,不是求某个固定谁的 FOLLOW 集,而涉及多个非终结符的 FOLLOW 集,所以建议对每个产生式对这 4 个规则都要考虑,不然很容易漏。
规则(1)看左侧为开始符;
规则(2)右侧看 B 后是否紧跟终结符;
规则(3)右侧看 B 后紧跟的是否有非终结符
规则(4)右侧看 B 是不是最后一个,或 B 后面的可以推出空串,间接最后一个
例题 4.4:求 FOLLOW 集
题目:
给定文法 G[S]:
(1)S -> eT|RT
(2)T -> DR|ε
(3)R -> dR|ε
(4)D -> a|bd
详解:
计算时,要同时考虑四个规则是否满足,就是都要考虑
对产生式(1):
- 1.满足规则(1),因为 S 是开始符号,可以得到 FOLLOW(S) = {#}
- 2.不满足规则(2)
- 3.满足规则(3),对 S -> RT,应把 FIRST(T) - {ε} = {a,b} 加到 FOLLOW(R);
- 4.满足规则(4),将 FOLLOW(S)={#} 加到 FOLLOW(T)
对产生式(2):
- 1.不满足规则(1)
- 2.不满足规则(2)
- 3.满足规则(3),对 T -> DR,应把 FIRST(R) - {ε} = {d} 加到 FOLLOW(D);
- 4.满足规则(4),将 FOLLOW(T)={#} 加到 FOLLOW(R)
对产生式(3):
- 1.不满足规则(1)
- 2.不满足规则(2)
- 3.不满足规则(3)
- 4.不满足规则(4),前后 R 和 R 一样不用加
对产生式(4):
- 1.不满足规则(1)
- 2.不满足规则(2)
- 3.不满足规则(3)
- 4.不满足规则(4)
最终结果:
FOLLOW(S) = {#}
FOLLOW(T) = {#}
FOLLOW(R) = {a, b, #}
FOLLOW(D) = {d, #}
(三)关于 SELECT 集 - 可选集
首先
SELECT 集的定义
注意区分 α 和 A
给定文法 G,对于产生式 A→α,α ∈ V*,则可选集 SELECT(A→α) 有:
(1)若 α ≠ ε,且 α ≠+ ε,则 SELECT(A→α) = FIRST(α)
(2)若 α ≠ ε,但 α =+ ε,则 SELECT(A→α) = FIRST(α) ∪ FOLLOW(A)
(3)若 α = ε,则 SELECT(A→α) = FOLLOW(A)
描述(关键):
(1)第1条说,α ≠ ε,且通过1次或多次推不出 ε,SELECT(A→α) = FIRST(α)
(2)第2条是,α ≠ ε,α 经有限步可推出 ε,注意是一个 α,一个 A,SELECT(A→α) = FIRST(α) ∪ FOLLOW(A)
(3)第3条是说如果 α 本身就是 ε,SELECT(A→α) = FOLLOW(A)。
用表达式描述:

例题 4.5:求 SELECT 集
题目:
给定文法 G[S]:
(1)S -> aA
(2)S -> c
(3)A -> aAS
(4)A -> ε
详解:
对(1)使用规则(1),得 SELECT(S -> aA) = FISRT(aA) = {a},此时虽然 A 可以推出 ε,但规则中指的是整体 aA
对(2)使用规则(1),得 SELECT(S -> c) = FISRT(c) = {c}
对(3)使用规则(1),得 SELECT(A -> bAS) = FISRT(bAS) = {b}
对(4)使用规则(3),得 SELECT(A -> ε) = FOLLOW(A) = {a, c, #}
下面再回顾一下 FOLLOW 集的求法。
对本题求 FOLLOW(A) ,先求出 FIRST(S) = {a, c}:
对产生式(1):
- 1.满足规则(1),S 是开始符号,FOLLOW(S) 为 {#}
- 2.不满足规则(2)
- 3.不满足规则(3)
- 4.满足规则(4),FOLLOW(S) = {#} 加到 FOLLOW(A)
对产生式(2):
- 1.不满足规则(1)
- 2.不满足规则(2)
- 3.不满足规则(3)
- 4.不满足规则(4)
对产生式(3):
- 1.满足规则(1)
- 2.不满足规则(2)
- 3.不满足规则(3),FIRST(S) - {ε} = {a, c} 加到 FOLLOW(A)
- 4.不满足规则(4)
对产生式(4):
- 1.不满足规则(1)
- 2.不满足规则(2)
- 3.不满足规则(3)
- 4.不满足规则(4)
综合可以看出 FOLLOW(A) = {a, c, #}
(四)关于 LL(1) 文法
LL(1) 文法名称的含义:
| 名称 | 含义 |
|---|---|
| 第一个L | 从左到右扫描输入串 |
| 第二个L | 使用最左推导方法 |
| 1 | 只需查看一个输入符号便可决定选择哪个产生式进行推导 |
文法是 LL(1) 文法的充分必要条件:
若某文法是LL(1)文法,那么它能够唯一确定选用的产生式
判断文法是否是 LL(1) 文法步骤如下:
- 求出能推出ε的非终结符;
- 计算FIRST集;
- 计算FOLLOW集;
- 计算SELECT集;
- SELECT集相交是否为空。
例题 4.6:判断文法是否是 LL(1) 文法
题目:
给定文法 G[S]:
(1)E -> TE'
(2)E' -> ATE'|ε
(3)T -> FT'
(4)T' -> MFT'|ε
(5)F -> (E)|i
(6)A -> +|-
(7)M -> *|/
答案:
FIRST 集,FOLLOW 集,SELECT 集如下
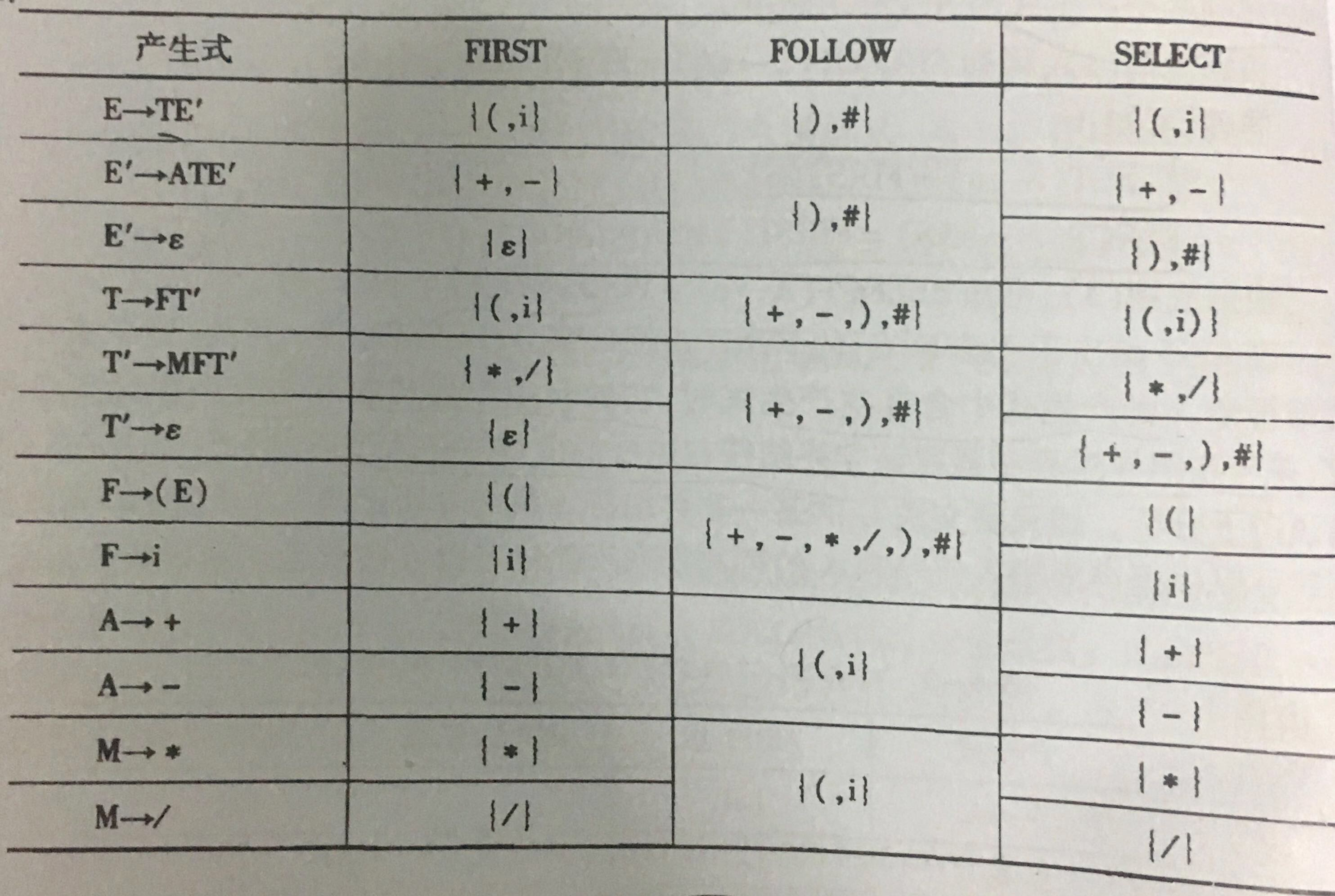
(图片来自教材:《编译原理》张晶老师版)
非常要注意的是:
我们知道判断是否为 LL(1) 文法条件是:根据同一非终结符的 SELECT 集是否相交,相交不是,不相交则是。
那么 E 和 E' 的统一非终结符吗?LL(1) 是否为空,要比较 SELECT(E) 和 SELECT(E') 吗?
答案是:不是统一非终结符,不用也不能比较他俩。因为他俩没有关系,E' 类似于是中间变量,用其他的字母替换也不影响此文法的功能
详解:
因为:
SELECT(E' -> ATE') ∩ SELECT(E' -> ε)= ∅
SELECT(T' -> MFT') ∩ SELECT(T' -> ε)= ∅
SELECT(F -> (E)) ∩ SELECT(F -> i)= ∅
SELECT(A -> +) ∩ SELECT(A -> -)= ∅
SELECT(M -> *) ∩ SELECT(M -> /)= ∅
所以 SELECT 集相交是否为空,文法 G[S] 是 LL(1) 文法
(五)关于 LL(1) 分析法(预测分析法)
LL(1) 分析法,也称预测分析法,采用这种方法的分析器由一张分析表、一个分析栈和一个控制程序组成,图形化比表示为:

(图片来自教材:《编译原理》张晶老师版)
这个语法分析过程完全由**预先根据文法设计的分析表 M **以及 分析栈S 进行控制(控制程序)
分析表和控制程序: 对于不同的文法,会有不同的分析表 M,但这种语法分析方法的总控程序是一样的。
分析栈: 分析栈 S 用于存放文法符号。分析开始时,栈底先放一个 ‘ # ’,然后,放进文法的开始符号。随着分析的展开,放入相应符号。
关于分析表:
(1)分析表是一个二维数组 M[A,a],其中 A 是非终结符,a 是终结符或 #。
(2)M[A,a] 中若有产生式,表明 A 可用该产生式推导,以求与输入符号 a 匹配。
(3)M[A,a] 中若为空,表明 A 不可能推导出与 a 匹配的字符串。
怎么求分析表:
对文法 G 的每个产生式 A->α 执行以下步骤:
(1)若 a∈SELECT (A->α), 则把 A->α 加至 M[A,a] 中;
(2)把所有无定义的 M[A,a] 标上“出错标志”。
为了使表简化,表中空白处为出错。
关于控制程序:
控制程序在任何时候都是按分析栈栈顶符号 X 和当前的输入符号 a 行事的。对于任何(X,a),总控程序每次都执行下述三个动作之一:
- 若 X=a=‘ # ’,则分析成功。
- 若 X=a≠‘ # ’,则把 X 从栈顶弹出,让 a 指向下一个输入符号。
- 若 X 为一非终结符,则查分析 表M。若 M[X,a] 中为A—产生式,将 A 自栈顶弹出,将产生式右部符号串按逆序逐一推入栈中;当产生式为 A 时,则只将 A→ε弹出即可。若 M[X,a] 中为空,则调用出错处理程序。
例题:求预测分析表
题目(同上):
给定文法 G[S]:
(1)E -> TE'
(2)E' -> ATE'|ε
(3)T -> FT'
(4)T' -> MFT'|ε
(5)F -> (E)|i
(6)A -> +|-
(7)M -> *|/
答案:
FIRST 集,FOLLOW 集,SELECT 集如下

(图片来自教材:《编译原理》张晶老师版)
文法 G(E) 的预测分析表 M:
提示: 根据 SELECT 可选集对应

(图片来自教材:《编译原理》张晶老师版)
用上述文法 G(E) 识别句子 i+i*i 的分析过程:
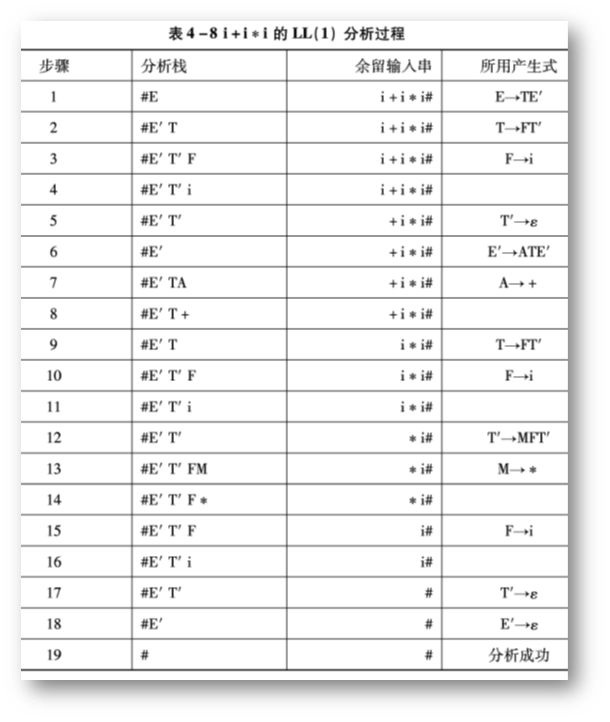
(图片来自教材:《编译原理》张晶老师版)
详细分析:
(1)执行顺序:
步骤 1 为初始化,分析栈放入 # 后,放入开始符号;
根据分析栈栈首为 E,余留串首为 i,可定位到 E -> TE',逆序放入分析栈;
此时,栈首为 T,串首为 i,根据 T 和 i 定位到 T -> FT',逆序放入;
此时,栈首为 F,串首为 i,根据 F 和 i 定位到 F -> i,只有一个,直接放入;
此时,栈首为 i,串首为 i,则是识别成功,余留串中第二个,依次...
(2)再根据预测分析表 M 选出产生式,没有则调用出错处理程序
(3)注意一定要逆序入分析栈,为什么要逆序放入分析栈呢?
因为是 LL(1) 分析法, LL(1) 文法是从左向右扫描,第二个L是最左推导的意思,最左推导就是每次都先推最左边的一个非终结符。LL(1) 分析法是每次拿出分析栈的栈顶,如果不逆向最左端的非终结符就会在栈中,没法拿出来继续推导。通过逆序,可以实现每次拿出栈顶,就是拿出最左非终结符,就可以实现最左推导
再回顾 LL(1) 文法名称的含义:
| 名称 | 含义 |
|---|---|
| 第一个L | 从左到右扫描输入串 |
| 第二个L | 使用最左推导方法 |
| 1 | 只需查看一个输入符号便可决定选择哪个产生式进行推导 |
(4)当分析栈栈顶元素和输入串最左端相同时,符合,分析栈栈顶出栈,识别下一个余留输入串。
(六)关于递归下降法
对于 LL(1) 文法的分析可以采用两种方法:
- 一种是上一节介绍的 LL(1) 分析法,它利用 LL(1) 分析表和语法分析栈来实现
- 一种是递归下降法,它利用一组可相互递归调用的子程序来实现
递归下降法基本思想
为每一个非终结符编制一个子程序,
子程序的名字表示一个产生式左部的非终结符,
程序体是按该产生式右部的符号串顺序编写的。
每匹配一个终结符,则再读入下一个符号,对于产生式右部的每个非终结符,则调用相应子程序。
当一个非终结符对应多个候选式时,子程序体按 SELECT 集决定选用哪个候选式。
例题:递归下降法
题目:
给定文法 G[S]:
(1)S -> AaB|Bb
(2)A -> aD|D
(3)B -> d|e|ε
(4)D -> fD|g
答案:
FIRST 集,FOLLOW 集,SELECT 集如下
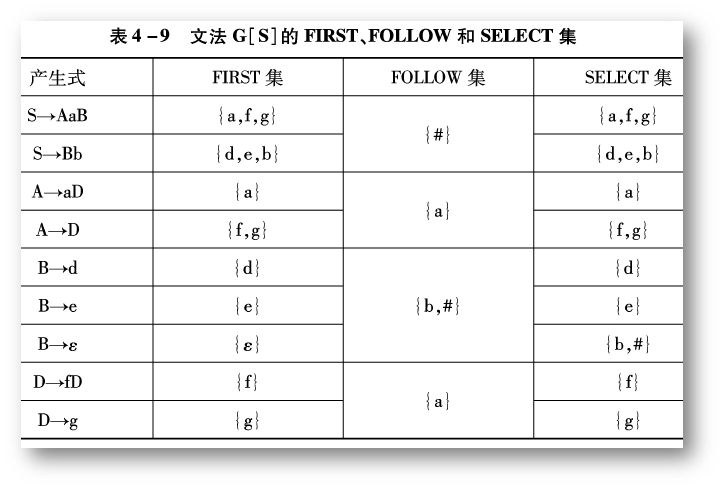
(图片来自教材:《编译原理》张晶老师版)
因为:

可知此文法是 LL(1) 文法
递归下降法分析:
主函数:
scan;
call S;
if token = '#' then accept
else error;
scan 表示调用词法分析程序读入下一个单词至变量 token;
error 表示报错处理。
函数 S:
if token in {a,f,g}
then {
call A;
match(a);
call B;
}
else if token in {d,e,b}
then {
call B;
match(b);
}
else error;
match(a) 表示若当前输入单词为 a,则调用 scan,否则调用 error
上述递归下降分析器完全是按照产生式的形式编写的,处理针对四非终结符要编写四个函数,还要有主函数。
当分析句子时,需要调用许多与文法非终结符对应的函数。
递归下降法的优点:
(1)分析器编写速度快
(2)由于分析器非紧密对应性,容易保证语法分析器的正确性,至少使得任何错误都变得简单和易于发现
递归下降法的缺点:
(1)在语法分析期间高深度的递归调用影响了分析器的效率,许多时间需要花费在递归子程序之间的连接上
(2)如果瞎用的高级语言不允许递归,那么就不能使用递归下降法,可以用 LL(1) 分析法


 浙公网安备 33010602011771号
浙公网安备 33010602011771号