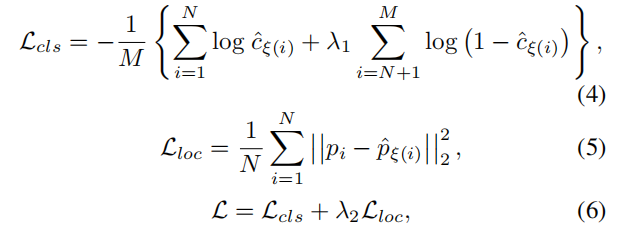有监督/无监督人群计数的几个模型
有监督/无监督计数
基于深度学习的方法主要可以分为两类:密度估计方法和检测+回归方法。
- 密度估计方法:这是最常见的方法,其主要思路是学习一个将输入图像映射到人群密度图的函数。密度图上每个像素的值代表了该位置的人群密度。通过对整个密度图求和,可以得到整个图像中的人数。为了得到密度图,需要对人头的位置进行标注,并生成对应的密度图作为训练目标。一些典型的网络如MCNN(Multi-column Convolutional Neural Network)、CSRNet(Convolutional Social Relation Network)都属于这一类。
- 检测+回归方法:这类方法将人群计数问题分解为两个子问题:人头检测和人头大小回归。首先,通过一个人头检测网络找出图像中所有可能的人头位置,然后通过回归网络预测每个人头的大小。将所有预测的人头大小求和,就可以得到总的人数。这种方法可以处理人群密度变化大的情况,但对于大量遮挡的场景可能会有困难。
对于人群定位问题,一种常见的方法是通过寻找密度图的局部最大值来定位人头。此外,也有一些方法直接利用人头检测的结果进行定位。
1 MCNN (CVPR 2016)
直接扒了知乎上的介绍(
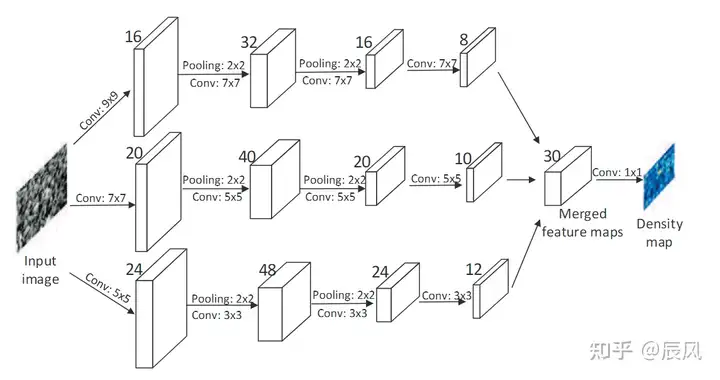
- MCNN,包含三列卷积神经网络,滤波器大小不同,三列对应具有不同的感受野,因此每个列cnn所学习的特征都能适应由于角度不同而导致的人头大小不均匀而引起的变化
- MCNN中,用1*1卷积代替全连接层,因此,模型的输入可以是任意大小的,很大程度上避免了失真的情况。网络的输出为密度图,通过对密度图进行积分即可计算得出总人数
F是密度图,N是图片数目
这个式子还没弄明白,先挖个坑吧
2 CSRNET (CVPR 2018)
2.1 改进&创新点
- Multi-column CNNs不好训练
- Multi-column CNNs各个column表现基本一致,并不像设想那样不同column负责不同密集度范围,存在有很多冗余
- 之前类似MCNN这样的Multi-Columns方式并没有一个更深的Single-Column网络性能好
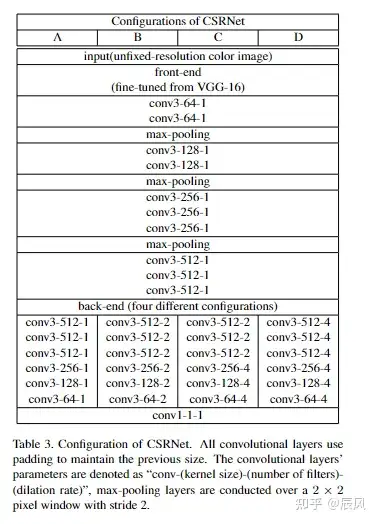
2.2 模型结构
利用了 Single-Column 的网络,VGG-16的前10层被用作特征提取器(front-end),而后端(back-end)使用空洞卷积(Dilated Convolution)来进一步处理这些特征并进行预测。
VGG:连续使用小的3x3卷积核和2x2的最大池化层,它将网络深度推进到16~19层。
在实践中,前端(特征提取器)通常会被冻结(即其权重在训练过程中不会更新),以保留在大规模数据集(如ImageNet)上学习到的通用特征。然后,我们训练后端(预测器)来适应我们的特定任务。
空洞卷积(Dilated Convolution)也被称为带孔卷积或膨胀卷积,是卷积神经网络中的一种操作,用于扩大卷积操作的感受野。空洞卷积在不增加计算复杂度和参数数量的情况下,提供了一种有效的方法来扩大网络的感受野。
感受野(Receptive Field)是指卷积神经网络中一个神经元对输入数据的感知范围。例如,在普通的卷积操作中,一个3x3的卷积核会对输入的3x3的局部区域进行感知;如果我们在卷积核之间加入“空洞”(实际上是在卷积核中插入零),我们可以在不增加参数的情况下,使得卷积核能够覆盖更大的区域,从而增大感受野。
空洞卷积的操作可以用一个参数d来表示“空洞”的大小,称为膨胀率(Dilation Rate)。当d=1时,空洞卷积就是普通的卷积;当d>1时,卷积核会以d-1的空洞来插入,形成更大的卷积核。例如,对于一个3x3的卷积核,如果d=2,那么在操作时,它会覆盖输入的5x5的区域。
Z是密度图,N是图片数目
3 AutoScale(ICCV 2019,(cv101冠军 2019)
3.1 改进&创新点
- 我们在做标注时,对于稀疏的人头直接标注,而对于那些密集区域的人头则会先进行放大再标注,而不同密集程度的区域应该有不同的缩放系数
- 人群密集程度都比较接*时,更有利于模型准确学习
3.2 模型结构
【分块大小变换+】AutoScale: Learning to Scale for Crowd Counting - 知乎 (zhihu.com)
挖个坑,之后有空一定复现一下
目前关于人群计数的研究主要是利用卷积神经网络(CNN)通过回归密度图进行计数,并取得了很大的进展。在密度图中,每个人用一个高斯斑点表示,最终的计数是通过对整个图的积分得到的。然而,要准确地预测密集区域上的密度图是困难的。一个主要问题是,密集区域上的密度贴图通常会累积附*许多高斯斑点的密度值,从而在一小部分像素上产生不同的大密度值。这使得密度图呈现具有显著图案移位的变化图案,并带来像素方向密度值的长尾分布。本文目标是在密度图中解决这一问题。具体提出了一种简单有效的学习缩放(L2S)模块,该模块将密集区域自动缩放到合理的贴*度水*(反映相邻人之间的图像*面距离)。L2S直接归一化不同斑块中的贴*度,从而动态地分离重叠的斑点,分解地面真实密度图中的累积值,从而缓解密度值的图案漂移和长尾分布。这有助于模型更好地学习密度贴图。通过寻找量化距离的局部最小值来探索L2S在定位人方面的有效性(w.r.t.。人员位置图),这与密度图回归有类似的问题。这种定位方法在基于定位的人群计数中也是新颖的。进一步引入了定制的动态交叉熵损失,显著改善了基于局部化的模型优化。大量实验表明,本文提出的AutoScale框架在三个拥挤的数据集上的回归和定位基准上都优于一些最先进的方法,并且在两个稀疏数据集上获得了非常有竞争力的性能。
4 P2PNet (ICCV 2021)
4.1 改进&创新点
- 在人群中定位个体比简单的计数更符合后续高层人群分析任务的实际需求。然而,现有的人群统计方法依赖于中间表示(即密度图或伪标签框)作为学习目标,这是反直觉和容易出错的。
- 在论文中,提出了一个基于点的框架,称为点对点网络(P2PNet),用于实现人群计数和个体定位。P2PNet抛弃了多余的步骤,直接预测一组点建议来表示图像中的头像,与真实值注释结果一致。
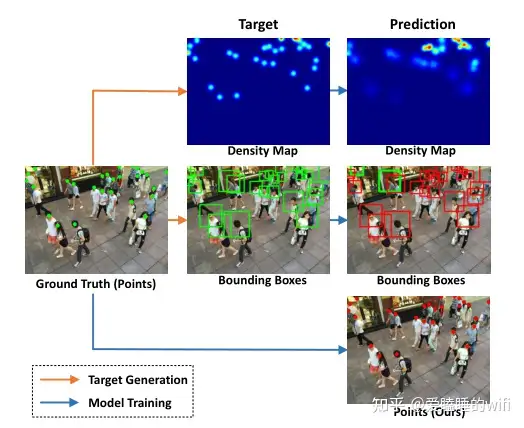
-
论文提出了一种称为密度归一化*均精度 (density Normalized Average Precision --nAP) 的新指标,为定位和计数错误提供综合评估指标。nAP 指标支持框和点表示作为输入(即预测或注释),没有上述缺陷。
-
作为这个新框架下的直观解决方案,论文开发了一种新方法来直接预测一组具有图像中头部坐标及其置信度的point proposals。具体来说,论文提出了一个点对点网络 (P2PNet) 来直接接收一组带标注的头部点用于训练,并在推理过程中预测点。为了使这样的想法正确工作,论文深入研究了ground truth target分配过程,以揭示这种关联的关键。结论是,无论是多个proposals 与单个ground truth匹配的情况,还是相反的情况,都会使模型在训练期间混淆,导致高估或低估计数。因此,论文建议通过匈牙利算法进行一对一匹配,将point proposals与其ground truth target相关联,未匹配的proposals 应归类为负样本。凭经验表明,这种匹配有利于改进 nAP 指标,作为论文在新框架下解决方案的关键组成部分。这种简单、直观和高效的设计产生了SOTA的计数性能和有前途的定位精度。
4.2 论文方法&网络结构
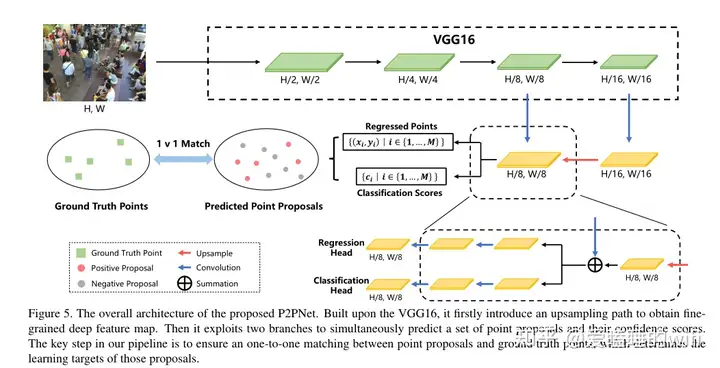
网络设计。如图所示,我们使用VGG-16 bn[36]中的前13个卷积层来提取深层特征。对于输出的特征图,我们使用最*邻插值将其空间分辨率提高2倍。然后将上采样的贴图与通过元素相加从横向连接获得特征图。该横向连接用于在第四卷积blcok之后减小特征图的通道维度。最后,合并后的特征图经过3×3卷积层以获得Fs,其中的卷积用于减少由于上采样引起的混叠效应。
拟建P2PNet的总体架构。在VGG16的基础上,首次引入上采样路径来获得细粒度的深度特征图。然后,它利用两个分支来同时预测一组点建议及其置信度得分。我们计划中的关键步骤是确保点建议和基本事实点之间的一对一匹配,这决定了这些建议的学习目标。
我们的P2PNet中的预测头由两个分支组成,这两个分支都输入了Fs,并分别产生点位置和置信度得分。为了简单起见,两个分支的架构保持不变,由三个与ReLU激活交织的堆叠卷积组成。我们从经验上发现,这种简单的结构产生了有竞争力的结果。
# the defenition of the P2PNet model
class P2PNet(nn.Module):
def __init__(self, backbone, row=2, line=2):
super().__init__()
# 若干次卷积(VGG)
self.backbone = backbone
# 类别分为背景和目标
self.num_classes = 2
# 1 image上的锚点数量
num_anchor_points = row * line
#求锚点的偏置
self.regression = RegressionModel(num_features_in=256, num_anchor_points=num_anchor_points)
#二分类任务
self.classification = ClassificationModel(num_features_in=256, \
num_classes=self.num_classes, \
num_anchor_points=num_anchor_points)
#锚点坐标生成器
self.anchor_points = AnchorPoints(pyramid_levels=[3,], row=row, line=line)
#特征金字塔网络,理解为把不同层的特征图(或者是不同通道的特征图)拿来加加减减
self.fpn = Decoder(256, 512, 512)
def forward(self, samples: NestedTensor):
# 向VGG输入图像 输出特征图
features = self.backbone(samples)
# 经fpn也是输出特征图
features_fpn = self.fpn([features[1], features[2], features[3]])
batch_size = features[0].shape[0]
# 求锚点偏置 & 进行二分类
regression = self.regression(features_fpn[1]) * 100 # 8x [32, 1024, 2]
classification = self.classification(features_fpn[1]) # [32, 1024, 2]
#generate锚点坐标
anchor_points = self.anchor_points(samples).repeat(batch_size, 1, 1)# [32,1024,2]
# decode the points as prediction
output_coord = regression + anchor_points # 预定义的点位置加上偏移量
output_class = classification
# pred_logits为每个点的置信度,pred_points为每个点的坐标信息
out = {'pred_logits': output_class, 'pred_points': output_coord}
return out
4.2.1 关于 regression 求预测点偏置
我们用 \(F_s\) 来表示从主干网输出的深度特征图, s是采样的步幅,\(F_s\) 的大小为HxW。 \(F_s\) 上的每个像素应该对应于输入图像中大小为s的patch。在那个patch中,我们首先引入了一组固定的参考点 \(R=\{R_k|k\in\{1,...,K\}\}\) 并且具有预定义的位置 \(R_k=(x_k,y_k)\) 这些参考点可以密集地分布在patch上,也可以仅仅设置在patch的中心,如图所示。
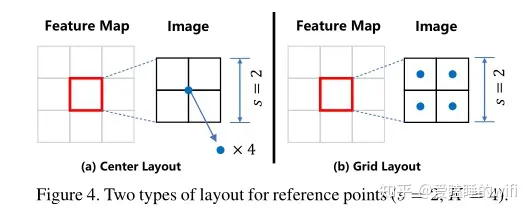
由于 \(F_s\) 上的每个位置有K个参考点,回归分支应该产生总共HxWxK个参考点。对每个参考点添加一个偏移量 \((\Delta_{jx}^k,\Delta_{jy}^k)\) 则每个参考点 \(p_j\) 的坐标计算如下:
对于ShanghaiTech数据集来说,由于输入模型的图像大小resize为128x128,而得到的特征图为16x16,对特征图中每个像素对应的patch设置4个参考点,则一张图像共有1024个参考点。
考虑一下这是在解决一个什么问题,首先经过若干次卷积之后图像已经变小了,在小图上锚点肯定是不精确的,这时候就加一个偏置,使得最后我们得到的人头的点处于精准的位置。而求每个锚点的偏置也是通过训练得到的,相当于让网络去学习然后学到预测点的偏置应该是多少。
4.2.2 点匹配
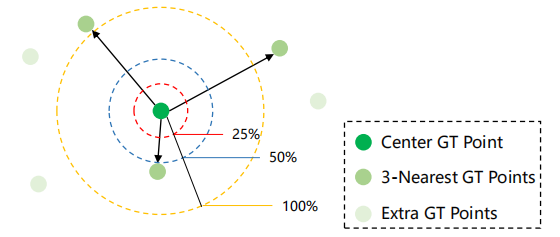
有个很牛逼的名字叫密度归一化。一个预测点 pˆj 只有在它可以匹配到某个ground truth pi 时才被归类为 TP。 匹配过程由基于像素级欧几里德距离的准则 (ˆpj , pi) 指导。 然而,直接使用像素距离来测量亲和度忽略了人群之间大密度变化的副作用。 因此,为此匹配标准引入了密度归一化,以缓解密度变化问题。
简单说来就是引入最*邻K(取3)个点,将它们的距离归一化。
用公式表示如下:
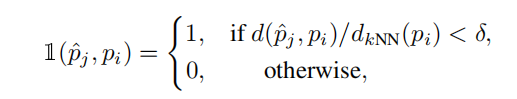
预测与ground truth匹配方案
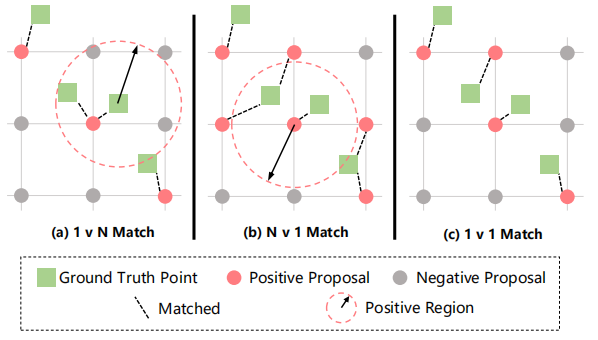
密度归一化之后,Ground Truth Point 与 Positive Proposal 建边,然后就变成了一个二分图的点匹配的问题
于是就是算法竞赛的内容了,我的老本行,这里可以直接跑网络流解决问题,然后考虑到是个二分图,论文里直接用的是匈牙利算法
4.2.3 损失函数