推导：PCA主成分分析&LDA线性判别分析
推导：PCA主成分分析&LDA线性判别分析
希望自己学过了就留个痕。
PCA和LDA都是在通过降维进行特征提取，PCA倾向于数据重构（就如名字一样 主成分分析），LDA倾向于数据分类（更好的将不同类别分开）。
考虑它具体在做什么事情，其实在每个样本进行中心化处理后（减去均值），一个样本就变成了一个距离向量来描述与中心的距离（PCA的中心是所有样本的中心，LDA的中心是类内的或总的），用协方差矩阵来描述样本之间的聚or散的程度。
现在求一个投影向量 \(w\) ，考虑把这些距离向量投影到一维上面，协方差矩阵就变成 \(1\times 1\) 的了，可以理解为此时的这个值（不妨设为 \(J\) ）就描述样本间聚or散的程度的（显然嘛）。
所以最后的思路就是用 \(w\) 以及样本数据把 \(J\) 表示出来，然后求偏导就能做了，具体看后面吧。
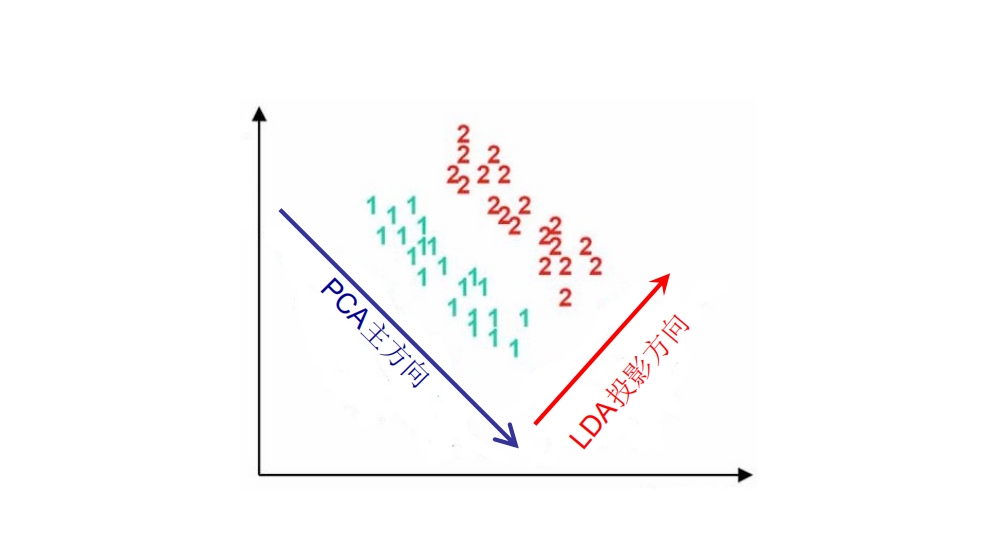
1 PCA主成分分析
PCA的目标是找到一组新的坐标轴，以此方式将原始数据空间进行旋转。新的坐标轴（或者叫做主成分）的选择是基于数据方差最大化的准则。这意味着第一主成分的选择是沿着数据具有最大方差的方向，第二主成分选择沿着与第一主成分正交并具有第二大方差的方向，依此类推。
现在我们有一个n维的数据集，并且我们已经计算了其均值并进行了中心化处理（即减去均值，使新的数据集的均值为0）。
假设我们想要找到第一主成分。我们可以定义一个单位向量u（u的转置乘以u为1），使得所有数据点到u的投影的方差最大。方差可以定义为：
这是所有点 \(x_i\) 在 u 上的投影的平方和，我们需要找到最大化V的u。这是一个优化问题，可以通过拉格朗日乘数法来解决，引入一个拉格朗日乘数λ，并将约束条件 \(u^T u = 1\) 带入。
我们需要找到最大化L的u，可以通过对u和λ分别求偏导，然后令它们等于零来解决。
这个优化问题要求我们找到一个向量u，使得在 \(u^T u = 1\) 满足约束条件下，最大化 \(u^T Cov(X)u\) 。\(Cov(X)\) 是数据的协方差矩阵，其中 \(X\) 是数据矩阵。
这个问题的解决方案是 \(Cov(X)\) 的特征向量，其对应的特征值是最大的。我们来看看这是如何工作的。
首先，我们计算 L 关于u和λ的偏导数，并将这些偏导数设为0。对于u，我们有：
这个公式可以整理为：
此时 L 关于u的偏导就为0了，考虑我们要最大化的是 \(u^T Cov(X)u=\lambda u^Tu\) ，所以最大化特征值就是最大化的方差值。按照特征值从大到小的顺序排列特征向量，我们就得到了主成分。显然不同特征值对应的特征向量是正交的，满足我们要求。
2 LDA线性判别分析
对于线性判别分析（Linear Discriminant Analysis, LDA），我们可以定义类内散度（within-class scatter）和类间散度（between-class scatter）的公式如下：
假设我们有C个类别，每个类别c有 \(N_c\) 个样本。每个样本是一个n维向量，记为x。每个类别的均值向量记为 \(\mu_c\) ，所有样本的全局均值向量记为 \(μ\) 。
-
类内散度（Within-class scatter）:
类内散度矩阵 \(S_w\) 可以通过下式计算：
\[S_w =\sum_c \sum_i (x_i - μ_c)(x_i - μ_c)^T \] -
类间散度（Between-class scatter）:
类间散度矩阵 \(S_b\) 可以通过下式计算：
\[S_b = \sum_c N_c (μ_c - μ)(μ_c - μ)^T \]
在进行LDA时，我们的目标是找到一个投影向量w，使得类间散度矩阵的迹最大化，同时类内散度矩阵的迹最小化。
因为投影过后的向量是一维的，所以trace可以去掉，等价于
我们注意到上述优化问题有一个隐含的约束，即 w 的长度（或说范数）应为1。这是因为，如果不加这个约束，我们可以通过无限增大 w 的长度来无限增大J(w)的值，这显然是无意义的。因此，我们的优化问题实际上是带约束的，形式如下：
化成无约束问题：
然后对w和λ分别求偏导并设为0，我们可以得到如下的等式：
因为 \(\max J(w)=\cfrac{w^TS_bw}{w^TS_ww}=w^T(S_bS_w^{-1}) w=\lambda w^Tw\) ，所以现在要最大化 \(\lambda\) ，即求 \(S_bS_w^{-1}\) 最大的特征值对应的特征向量。若降维到 \(m\) 维，就是求前 \(m\) 大的特征值对应的特征向量。
