树形 DP 学习笔记 1(树的重心)
树形 DP 学习笔记 1(树的重心)
前置芝士
会C++知道什么是树;- 会对树进行
dfs遍历; - 知道连通块是什么。
目录
- Part 1:概念
- Part 2:怎么求
Part 1:概念
概括
对于一棵有 n 个结点的无根树,找到一个点,使得把树变成以该点为根的有根树时,最大子树的结点数最小。换句话说,删除这个点后最大连通块的结点数最小。
分析
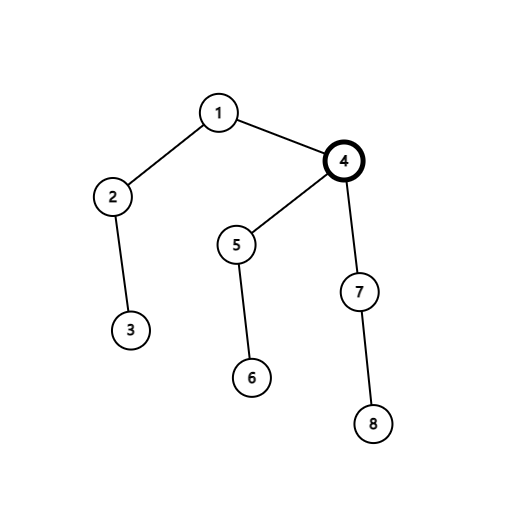
首先我们有一棵树,比如这个:
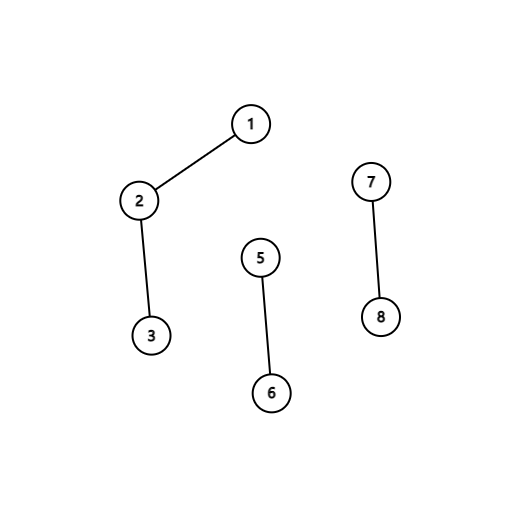
假设我们把被标黑的 4 号点删掉,那么剩下的几个点就变成这样:
所以这棵树变成了 3 个连通块,其中包含 1,2,3 的共 3 个点的连通块的点的数量最多。
如果我们把 1 号点删掉,那么图中还剩两个连通块,其中包含 4 号点的连通块的节点数最多,是 5。因为 3<5,所以删除 4 比删除 1更优。而求的就是最优的点。
Part 2:怎么求
文字分析
首先我们要知道,对于一个节点,把它删掉之后剩下的连通块中最大的连通块的节点数量是多少。
当我们把某一个点删掉时,一共会剩下这个节点的儿子数量 +1 个连通块。把这个点删掉之后,它的所有儿子都属于不同的子树,也就是不同的连通块。而加的 1 加的就是它祖先所属的连通块。
因此把这个节点删掉之后,剩下的连通块中最大的连通块的节点数量,就可以通过深度优先搜索来解决。求出来之后,可以直接在深搜的过程中更新答案。
代码实现
核心代码:
void dfs(int u,int fa){
if(g[u].size()==1&&u!=1) return ;//如果找到叶子了就可以直接返回
int maxf=0;
for(int i=0;i<g[u].size();++i){
int v=g[u][i];
if(v==fa) continue;
dfs(v,u);
f[u]+=f[v]+1;//f[i]表示以i为根的子树中有多少个节点
maxf=max(f[v],maxf);//更新最大值
}
int cur=max(n-1-f[u],maxf+1);//和祖先所属的连通块取max
if(cur<nowans) tot=0,ans[++tot]=u,nowans=cur;//如果当前答案更优,就可以直接将数组清零,这样做并不会不小心抹掉一些重要的数据
else if(cur==nowans) ans[++tot]=u;//否则继续更新数据
return ;
}
这样求出来之后,ans 中存的就是这棵树的所有重心了。
全部代码:
xxxxxxxxxx
using namespace std;
const int inf=0x3f3f3f3f;
int n,f[50001],ans[50001],tot=0,nowans=inf;
vector<int> g[50001];
void dfs(int u,int fa){
if(g[u].size()==1&&u!=1) return ;
int maxf=0;
for(int i=0;i<g[u].size();++i){
int v=g[u][i];
if(v==fa) continue;
dfs(v,u);
f[u]+=f[v]+1;
maxf=max(f[v],maxf);
}
int cur=max(n-1-f[u],maxf+1);
if(cur<nowans) tot=0,ans[++tot]=u,nowans=cur;
else if(cur==nowans) ans[++tot]=u;
return ;
}
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=1,u,v;i<n;++i){
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1,0);
sort(ans+1,ans+1+tot);
for(int i=1;i<=tot;++i) printf("%d ",ans[i]);
putchar('\n');
return 0;
}
练习
P2986 [USACO10MAR]Great Cow Gathering G
(目前好像只有一题)