经典算法——最短路径（Floyd+Dijkstra）

Floyd

时间复杂度：O(n^3)
简介：作为最短路算法中复杂度最高的算法没有之一，标志性结构三层循环，核心结构本质DP思想具 有动态规划的无后效性

他真的没有优点啦？！不，他有！

虽然SPFA，Dijkstra比他跑得快，但是只能算一个点到任意一点的最短路径，可Floyd是解决多源最短路的最佳方法，他能计算任意两点之间的最短距离

if(d[i][j]>d[i][k]+d[k][j])
	d[i][j]=d[i][k]+d[k][j]

想必这个代码我们在这个算法里并不陌生
设：总共有n个节点
我们在寻找的任意两点之间最短路时在中转点k我们为何能够确定下这个k点，是因为我们由三层循环已经判断了在这个点k前的路径是最短的，所运用的方法是O（n^2）的松弛
DP的无后效性，体现在k不仅是中转点还是一个状态变量，在选中k点前k已经作为i或j进行枚举了，所以说每次在确定下一个点的时候我们都保证了在1到k之间已经是最优路径
实现代码如下：

for(int k=1;k<=n;k++)
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(d[i][j]>d[i][k]+d[k][j])
				d[i][j]=d[i][k]+d[k][j];

Dijkstra

时间复杂度：O(n^3)
简介：利用的思想是贪心思想，准备阶段为将起点到各个点的距离都统计出来，核心阶段松弛遍历过的点，看是否能够作为中转点使其起点到另一个点的距离更短
借用大佬的图举个例子

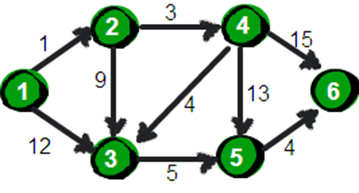
我们要想计算出1号点到各个点的最短路径
第一步：

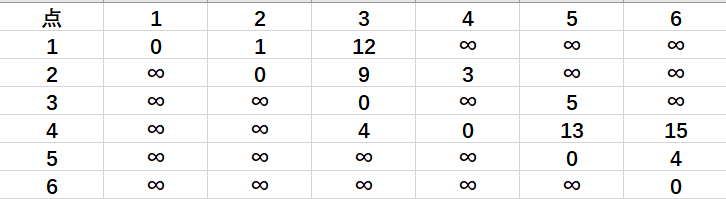
我们将两相邻点的距离进行统计
第二步：
将1到各点的距离用一个dis数组进行储存，不能直接到达的用∞表示
第三步：
寻找距离1点最近的点然后将最近的这个点当作中转点，然后重新计算经过该中转点后能够直接到达的点的距离，然后再次寻找此时距离1点最近的点，以此类推最后能确定1点到各个点的最近距离

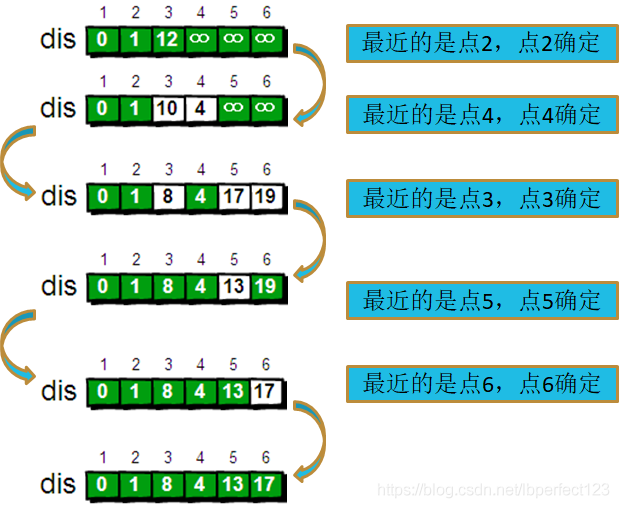
核心代码实现：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<queue>
using namespace std;
struct edge
{
int u,v,x;
} ed[1000010];
struct node
{
	int x,y;
bool operator <(const node & a)const
{
	return y>a.y;
}
};
priority_queue<node>que;
int head[1000010];
int dis[1000010];
int n,m,s,cnt;
void add(int x,int y,int z)
{
cnt++;
ed[cnt].u=head[x];
ed[cnt].v=y;
ed[cnt].x=z;
head[x]=cnt;
}
void dij()
{
for(int i=1; i<=n; i++)
	dis[i]=2147483647;
dis[s]=0;
que.push((node)
{
	s,0
});
while(!que.empty())
{
	node temp=que.top();
	que.pop();
	int x=temp.x,y=temp.y;
	if(y!=dis[x])
		continue;
	for(int i=head[x]; i; i=ed[i].u)
	{
		if(dis[ed[i].v]>dis[x]+ed[i].x)
		{
			dis[ed[i].v]=dis[x]+ed[i].x;
			que.push((node)
			{
				ed[i].v,dis[ed[i].v]
			});
		}
	}
}
}
int main()
{
cin>>n>>m>>s;
for(int i=1; i<=m; i++)
{
	int x,y,z;
	cin>>x>>y>>z;
	add(x,y,z);
}
dij();
for(int i=1; i<=n; i++)
	cout<<dis[i]<<" ";
return 0;
}

本蒟蒻目前只会这两种算法
至于SPFA和Bellman-Ford还需要努力
敬请期待！