强化学习

机器学习分类:

 

强化学习是机器学习中的一个领域，强调如何基于环境而行动，以取得最大化的预期利益

强化学习基础概念:
Agent :主体,与环境交互的对象,动作的行使者
Environment : 环境, 通常被规范为马尔科夫决策过程（MDP）
State :  环境状态的集合
Action : 环境下可行的动作集合，离散or连续
Reward :奖励, 有了反馈，RL才能迭代，才会学习到策略链

马尔可夫决策过程(MDP)

Markov Decision Processes:
马尔可夫决策过程是强化学习的理论基础
一个马尔可夫决策过程由一个五元组构成
      { S , A , 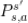 ,  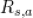       ,  γ }
S 表示状态集 (states)
A 表示动作集 (Action)      

表示状态 s 下采取动作 a 之后转移到 s' 状态的概率分布
表示状态 s 下采取动作 a 获得的奖励
γ 是衰减因子，表示的是随着时间的推移回报率的折扣

 

MDP的动态过程:

主体在状态s0选择某个动作a0∈A，主体根据概率         转移到状态s1，然后执行动作a1，...如此下去我们可以得到这样的过程：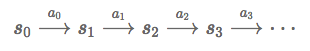

经过上面的转移路径，我们可以得到相应的回报函数和如下：

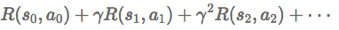
目标是选择一组最佳的动作，使得全部的回报加权和期望最大：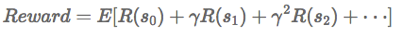

 

数学表示
策略(policy):
一个策略π就是一个从状态到动作的映射函数π:S↦A
确定性的policy（Deterministic policy）: a=π(s)　　
随机性的policy（Stochastic policy）: π(a|s)=P[At=a|St=t]　
状态值函数(value function):
给定初始状态s0和策略π后的累积折扣回报期望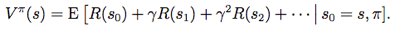

贝尔曼等式（Bellman Equations）:
对于一个固定的策略，它的值函数Vπ满足贝尔曼等式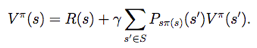

求解Vπ的目的是为找到一个当前状态s下最优的行动策略π服务的
最优值函数: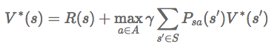

行动值Q函数:
表示在s状态下执行动作a作为第一个动作时的最大累计折扣回报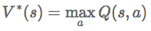

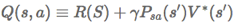
对应最优值函数的最优的策略为：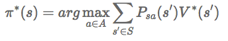

π∗是针对的是所有的状态s的，确定了每一个状态s的下一个动作a

求解方法

值迭代方法:
1 将每一个状态s的值函数V(s)初始化为0
2 循环直至收敛{  
            对于每一个状态s，对V(s)做更新
　　　　
}

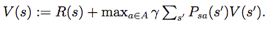
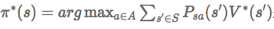
策略迭代方法:
1 随机初始化话一个S到A的映射π
2 循环直至收敛{
        2.1 令V:=Vπ
        2.2 对每一个状态s,对π(s)做更新
　　　　
           }

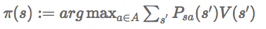
两者比较:
      规模较小的MDP，策略迭代一般能够更快的收敛
      规模较大的MDP（状态多），值迭代更容易些

MDP中的参数估计

 在许多实际问题中，状态转移概率分布Psa和回报函数R(s)不能显式的得到
假设我们已知很多条状态转移路径如下：

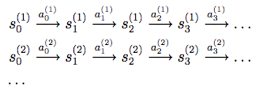
每条转移路径中的状态数都是有限的
 当获得了很多类似上面的转移路径后(样本)，我们可以用最大似然估计来估计状态转移概率。

                  分子表示在状态s通过执行动作a后到达状态s′的次数
                  分母表示在状态s我们执行动作的次数
对于未知的回报函数，我们令R(s)为在状态s下观察到的回报均值。

强化学习算法
Q-learning
Sarsa
Monte-carlo
Policy gradient
Temporal-difference
Deep-Q-Network(DQN)
TD-lambda
SARSA-lambda

强化学习特点：
无监督数据，只有奖励信号
奖励信号不一定实时，大部分情况奖励信号滞后
研究的时间序列
当前的行为影响后续数据分布
强化学习更加专注于在线规划，需要在探索（在未知的领域）和利用（现有知识）之间找到平衡