拉格朗日乘子法与KKT

通常我们需要求解的最优化问题有如下几类：

(i) 无约束优化问题，可以写为:

min f(x); 

(ii) 有等式约束的优化问题，可以写为:

min f(x);

s.t. hi(x) = 0; i =1, ..., n

(iii) 有不等式约束的优化问题，可以写为：

min f(x);

s.t. gi(x) <= 0; i =1, ..., n

hj(x) = 0; j =1, ..., m

 

一.无约束优化问题

 如果导数好求可以求导数,最优解就是导数为0的点,通常导数都不好求,可以用迭代法,梯度下降法,随机梯度下降法,牛顿法,拟牛顿法.可以参考:

http://www.cnblogs.com/meowmiao/p/6655912.html

 

二.有等式约束的优化问题

拉格朗日乘子法:

是一种寻找多元函数在其变量受到一个或多个条件的约束时的极值的方法。

可以将一个有n个变量与k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题。

这种方法中引入了一个或一组新的未知数，即拉格朗日乘数，又称拉格朗日乘子，或拉氏乘子，它们是在转换后的方程，即约束方程中作为梯度（gradient）的线性组合中各个向量的系数:

比如，要求f(x, y) ,在g(x,y)=c时的最大值时，我们可以引入新变量拉格朗日乘数 λ ，这时我们只需要下列拉格朗日函数的极值：

拉格朗日乘数法所得的极点会包含原问题的所有极值点，但并不保证每个极值点都是原问题的极值点。

例如:

求此离散分布的最大熵：

所有概率的总和是1，因此我们得到的约束是g(p)= 1即

可以使用拉格朗日乘数找到最大熵（概率的函数）。对于所有的k从1到n，要求

由此得到

计算出这n个等式的微分，我们得到：

这说明pi都相等（因为它们都只是λ的函数）。解出约束∑k pk = 1，得到

因此，使用均匀分布可得到最大熵的值。

 

三.有不等式约束的优化问题

KKT条件(Karush-Kuhn-Tucker Conditions)

KKT是广义拉格朗日乘子法

对于以下非线式最优化问题：

f(x)是需要最小化的函数，gi(x) ( i = 1 , … , m ) 是不等式约束，hj(x)( j = 1 , … , l )是等式约束，m和l分别为不等式约束和等式约束的数量。

KKT求解SVM:

要求下列函数最小化

改写为目标函数可微的约束优化问题

求解上述问题的拉格朗日对偶，得到简化的问题

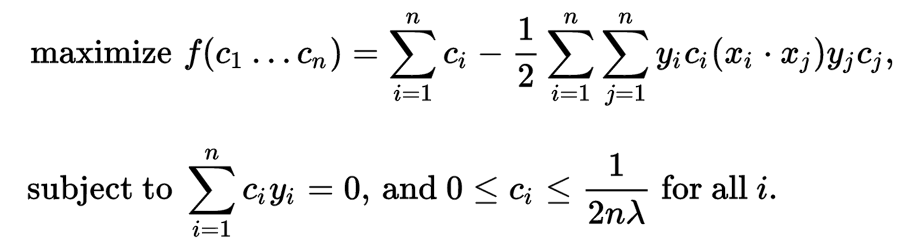
由于对偶最小化问题是受线性约束的 c i 的二次函数，所以它可以通过二次规划算法高效地解出。 这里变量 c i 定义为满足

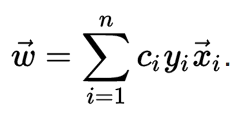
此外，当 xi  恰好在间隔的正确一侧时 c i = 0，且当 xi 位于间隔的边界时 0 < c i < ( 2 n λ ) − 1 。因此， w 可以写为支持向量的线性组合。 可以通过在间隔的边界上找到一个 xi并求解

得到偏移量b.