如何使用图卷积网络对图进行深度学习
在高度复杂的信息图结构上进行机器学习是困难的。
图卷积GCN是一种神经网络,可以被用于直接在图上进行工作,同时也借助了他们的结构信息。
接下来,将介绍GCN以及信息是如何通过GCN的隐藏层进行传播的,以及这个机制如何生成有用的特征表示的。
首先介绍一下,什么是图神经网络?
图神经网络是个在图上学习的一种网络架构。事实上,它们非常强大,即使是一个随机启动的两层GCN也可以产生网络中节点的有用特征表示。
举个例子:左侧是真实的网络结构,右侧是图的节点特征表示
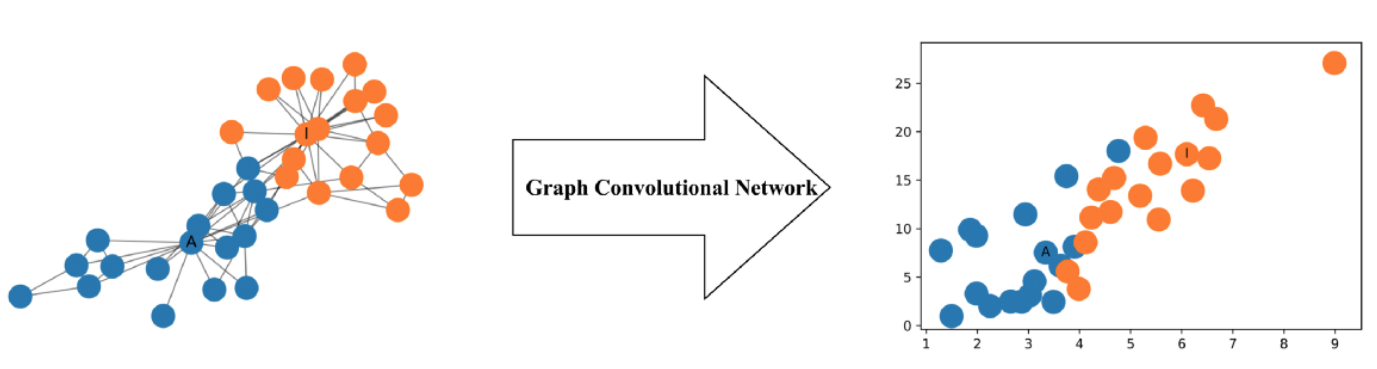
图卷积网络(GCN)是一种对图进行操作的神经网络。给定一个图G = (V, E), GCN的输入为:
- 输入特征矩阵X:N*F, 特征矩阵X。N表示的是节点的数量;F是每个节点的输入特征数量;
- 邻接矩阵A: N*N矩阵表示的是图结构,也即用A来表征。
- 隐藏层H:表示的是特征矩阵。每层的H可以被写作
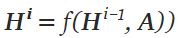
值得注意的是,H0,即第一层的特征矩阵就是输入的X;
f表示的是一种propagation rule,即传播规则。
每个H对应的是N*F特征矩阵,每行都是一个节点的特征表示;
在这种方式下,特征就会变得越来越抽象在每个连续层。
在这种框架下,不同GCN的变化唯一不同的是propagation rule的变化;即传播规则的变化;
最简单的传播规则
一个最简单的传播规则定义如下:
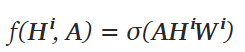
W是权重矩阵;维度Fi*Fi+1 也就是,权重矩阵决定了下一层特征表示的维度;
sigma是激活函数,比如RELU函数;
最简单的版本
- i=1的时候,f就是输入特征矩阵的函数
- sig可以是一个恒等函数,
- 选择权重,可以是AHW=AXW=AX
换句话而言,f(X,A) = AX; 这个传播规则未免有些太简单了。接下来会讲一些更为复杂的传播规则;
另一方面,AX现在等同于一个多层感知机的输入层;
一个简单的有向图的例子
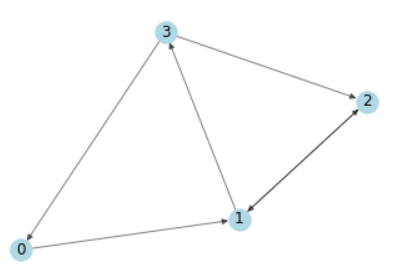
可以使用numpy邻接矩阵表示:
1 A = np.matrix([ 2 [0, 1, 0, 0], 3 [0, 0, 1, 1], 4 [0, 1, 0, 0], 5 [1, 0, 1, 0]], 6 dtype=float 7 )
接下来是特征的表示:
我们基于他们的index生成两个特征,这样可以方便我们接下来手动计算检验
1 X = np.matrix([ 2 [i, -i] 3 for i in range(A.shape[0]) 4 ], dtype=float)
X Out[6]: matrix([[ 0., 0.], [ 1., -1.], [ 2., -2.], [ 3., -3.]])
应用传播规则:
我们现在有了一个图,有了邻接矩阵A,以及一系列的输入X,接下来可以应用传播规则:
1 A * X 2 Out[7]: 3 matrix([[ 1., -1.], 4 [ 5., -5.], 5 [ 1., -1.], 6 [ 2., -2.]])
现在,所有的节点表示是它每个邻居节点的求和;
换句话说,图卷积层将每个节点表示成每个邻居节点的聚合;
注意的是,一个节点n是一个节点v的邻居,需要存在一个边从v到n。也就是流出方向矩阵。
这样做的问题及改进:
1. 这个表示没有包括自身——A+I;
2. 度比较大的节点特征表示可能也比较大,会造成梯度的小时和爆炸;——归一化处理


