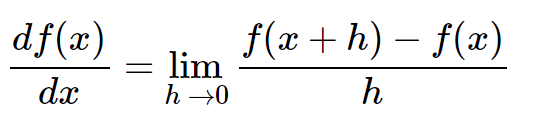对于backpropagation的理解

来自:

https://cs231n.github.io/optimization-2/

动机。在本节中，我们将通过对反向传播的直观理解来发展专业知识，反向传播是一种通过递归应用链式法则来计算表达式梯度的方法。理解这个过程及其微妙之处对于理解并有效地开发、设计和调试神经网络至关重要。

 

问题陈述。本节研究的核心问题是:我们已知一些函数f(x)，其中x是一个输入向量，我们感兴趣的是计算f在x处的梯度(即∇f(x))。

 

动机。回想一下，我们对这个问题感兴趣的主要原因是在神经网络的特定情况下，f将对应于损失函数(L)，而输入x将由训练数据和神经网络权值组成。例如，损失可以是SVM损失函数，输入是训练数据(xi,yi)，i=1…N，权值和偏差W,b。注意(在机器学习中通常是这样的)我们认为训练数据是给定的和固定的，权重是我们可以控制的变量。因此，尽管我们可以很容易地使用反向传播来计算输入示例xi上的梯度，但在实践中，我们通常只计算参数(如W、b)的梯度，因此我们可以使用它来执行参数更新。然而，我们会在后面的课程中看到，xi上的梯度有时仍然是有用的，例如，用于可视化和解释神经网络可能在做什么。

 

如果你来这类和您熟悉推导梯度与链式法则,我们仍然愿意鼓励你至少浏览这一节,因为它提供了一个难得的反向传播向后流在实值电路和任何见解您将获得可以帮助你在整个类。

 

Simple expressions and interpretation of the gradient

让我们从简单开始，以便为更复杂的表达式开发表示法和约定。考虑两个数字f(x,y)=xy的简单乘法函数。推导任意一个输入的偏导数是一个简单的微积分问题:

 

 

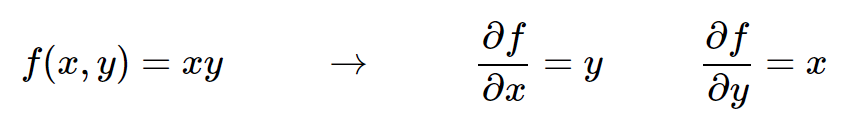
解释。记住导数所告诉你的:它们表示一个函数相对于这个变量的变化率，这个变量围绕着一个在某一点附近的无穷小区域: