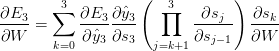循环神经网络教程，第3部分-通过时间和消失梯度的反向传播
在本教程的前一部分中，我们从无开始实现了一个RNN，但是没有详细说明反向传播(BPTT)算法是如何计算梯度的。在这一部分中，我们将简要概述BPTT，并解释它与传统的反向传播有何不同。然后我们将尝试理解消失梯度问题，这导致了LSTMs和GRUs的开发，这是目前在NLP(和其他领域)中使用的两个最流行和强大的模型。梯度消失问题最初是由Sepp Hochreiter在1991年发现的，最*由于深层架构应用的增加而再次受到关注。
Backpropagation Through Time (BPTT)
让我们快速回顾一下RNN的基本方程。注意，从o到y的符号略有变化。这只是为了和我引用的一些文献保持一致。
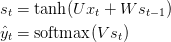
我们还将损失或误差定义为交叉熵损失，由:
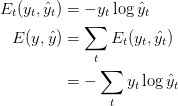
这里，y_t是t时刻正确的词，而yh_t是我们的预测。我们通常将整个序列(句子)视为一个训练示例，因此总损失只是每个时间步(单词)上损失的总和。
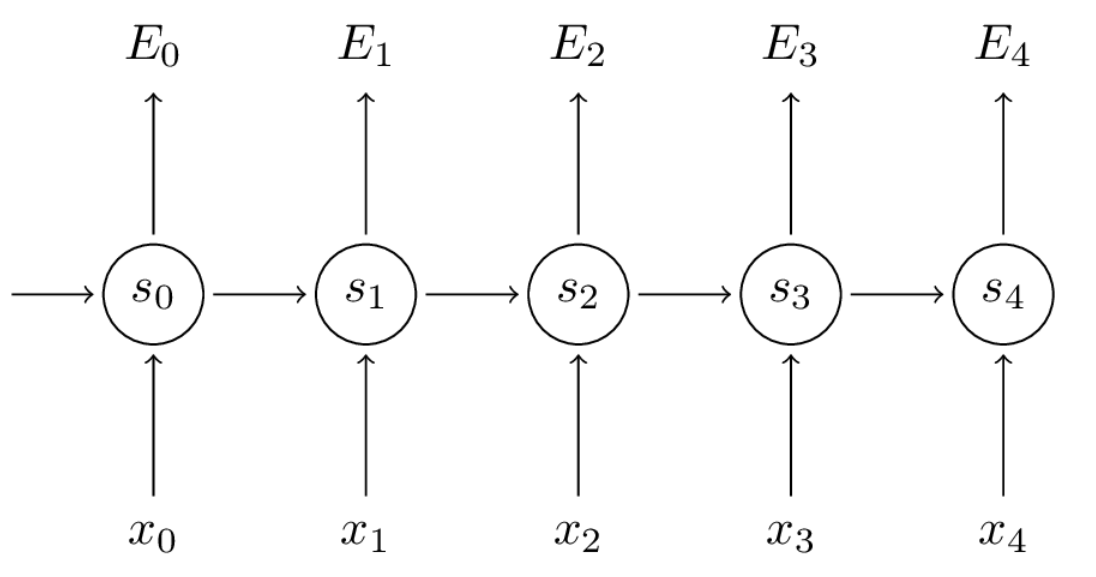
记住我们的目标是计算误差相对于参数U V W的梯度然后用随机梯度下降法学习好的参数。就像我们对误差进行累加一样，我们也对一个训练示例的每个时间步长进行累加: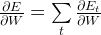
为了计算这些梯度，我们使用链式求导法则。这就是反向传播算法从误差开始向后应用。在这篇文章的其余部分，我们将使用E_3作为一个示例，只是为了使用具体的数字。
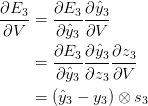
我们把每个时间步长对梯度的贡献加起来。换句话说，因为到我们关心的输出，每一步都要用到W，所以我们需要将t=3的梯度通过网络反向传播，直到t=0:
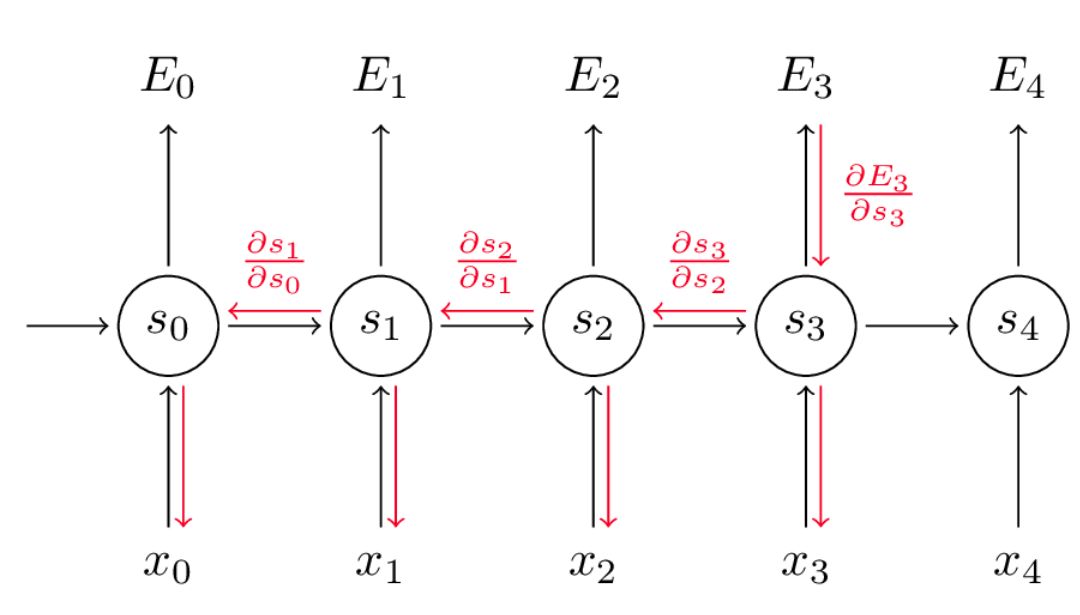
请注意，这与我们在深度前馈神经网络中使用的标准反向传播算法完全相同。关键的区别在于，我们在每个时间步长下将W的梯度加起来。在传统的神经网络中，我们不跨层共享参数，所以我们不需要对任何东西求和。但在我看来，BPTT只是展开RNN上的标准反向传播的一个花哨名称。就像反向传播一样你可以定义一个向后传递的向量，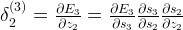
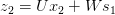
这也会让你明白为什么标准的RNNs很难训练:序列(句子)可能很长，可能有20个单词或更多，因此你需要通过许多层向后传播。在实践中，许多人将反向传播截断为几个步骤。
这也会让你明白为什么标准的RNNs很难训练:序列(句子)可能很长，可能有20个单词或更多，因此你需要通过许多层向后传播。在实践中，许多人将反向传播截断为几个步骤。
The Vanishing Gradient Problem
在本教程的前几部分中，我提到了RNNs在学习长时间的依赖关系——单词之间的相互作用时存在困难。这是有问题的，因为一个英语句子的意思通常是由不太接*的单词决定的:“the man who wear a wig on his head goes inside”。这个判决实际上是关于一个男人进去，而不是关于假发。但是一个普通的RNN不太可能捕捉到这样的信息。为了理解为什么，让我们来仔细看看我们上面计算的梯度:
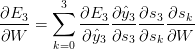
请注意,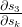
本身就是一个链式法则!例如,。还要注意,
因为我们正在一个矢量函数的导数对一个向量,其结果是一个矩阵(称为雅可比矩阵)的元素都是逐点偏微分。我们可以把上述梯度:
结果是(我不会在这里证明，但本文会详细说明)上面雅可比矩阵的2范数，你可以把它想象成一个绝对值，它的上界是1。这很直观，因为我们的tanh(或sigmoid)激活函数将所有值映射到-1和1之间的范围内，并且其导数也以1为界(在sigmoid的情况下为1/4):
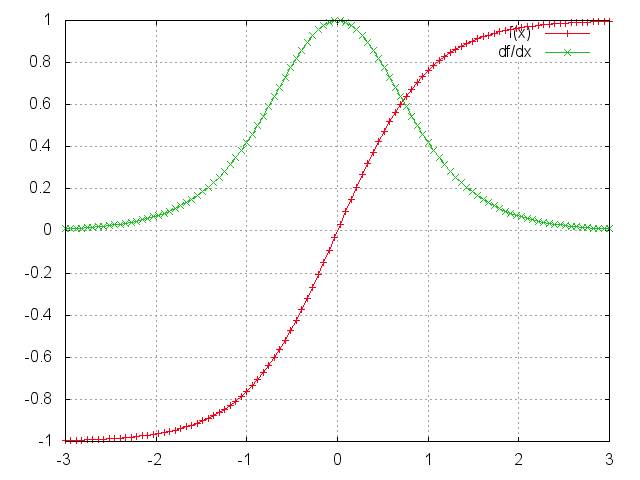
可以看到，\tanh和s形函数的导数两端都是0。他们接*一条*的线。当这种情况发生时，我们就说相应的神经元饱和了。它们的梯度为零，并将之前图层中的其他梯度推向0。因此，对于较小的矩阵和多重矩阵乘法(特别是t-k)，梯度值以指数速度缩小，最终在几个时间步后完全消失。“远处”步骤的梯度贡献变成零，这些步骤的状态对您正在学习的内容没有帮助:您最终没有学习长期依赖关系。梯度消失并不只属于rnn。它们也发生在深度前馈神经网络中。只是rnn往往非常深奥(就像我们的例子中的句子长度一样深奥)，这使得这个问题更加常见。
很容易想象，根据我们的激活函数和网络参数，如果雅可比矩阵的值很大，我们可以得到爆炸而不是消失的梯度。事实上，这就是所谓的爆炸梯度问题。消失梯度比爆炸梯度受到更多关注的原因有两方面。首先，爆炸式渐变很明显。我们的梯度将变成NaN(不是一个数字)，您的程序将崩溃。其次，裁剪梯度在一个预先定义的阈值(在本文中讨论)是一个非常简单和有效的解决爆炸梯度。消失梯度是更有问题的，因为它不明显何时出现或如何处理它们。
幸运的是，有一些方法可以解决梯度消失的问题。适当的初始化W矩阵可以减少梯度消失的影响。所以能正规化。一种更可取的解决方案是使用ReLU而不是tanh或sigmoid激活函数。ReLU导数是一个常数，要么0要么1，所以它不太可能受到梯度消失的影响。一个更流行的解决方案是使用长短期内存(LSTM)或门控循环单元(GRU)架构。LSTMs在1997年首次被提出，现在可能是NLP中使用最广泛的模型。GRUs于2014年首次提出，是LSTMs的简化版本。这两种RNN架构都被明确设计用于处理梯度消失和有效学习远程依赖关系。我们将在本教程的下一部分中介绍它们。
