Efficient and Straggler-Resistant Homomorphic Encryption for Heterogeneous Federated Learning

为异构联邦学习提供高效且抗掉队者的同态加密技术（INFOCOM 24' (CCF A)）

本文的结构和逻辑清晰，结构设置、文笔以及实验设置和实验分析都值得收藏和反复学习！！！

摘要

同态加密 (HE) 被广泛用于加密模型更新，但会产生很高的计算和通信开销。为了减少这些开销，有人提出了打包 HE（PHE），将多个明文加密为一个密文。然而，PHE 的原始设计并没有考虑不同客户端之间的异质性（这是跨孤岛 FL 中的一个固有问题），这往往会导致训练效率降低，收敛速度变慢，出现掉队者。
在这项工作中，我们提出了 FedPHE，这是一个高效打包的同态加密 FL 框架，具有安全的加权聚合和客户端选择功能，可解决异构性问题。

通过使用具有稀疏化功能的 CKKS，FedPHE 可以考虑局部更新对全局模型的贡献，从而实现高效的加密加权聚合。
为了减轻落后效应，我们设计了一种基于草图的客户端选择方案，以挑选具有异构模型和计算能力的代表性客户端。

总结
本文方案的安全假设：假定 PS 不会与任何客户端串通，PS 和客户端都是诚实但好奇的
本文的工作集中在三方面：
1. 使用打包同态加密以及稀疏化方法（使用打包密文和掩码方式），降低了通信量，提升了效率
2. 基于LSH草图根据参数计算权重，实现密文下的加权聚合
3. 基于LSH草图进行聚类，每个类中根据服务器的历史参数接收速度选出一个最快的客户端作为下一轮参与聚合的客户端，从而减轻掉队者问题

引言

HE在执行计算密集型加密操作（例如，模乘法和多项式约简）时会产生大量的计算和通信开销，并生成比输入明文大得多的密文。
现有的 PHE 解决方案虽然有效，但在很大程度上忽略了参与客户端的异质性 [18, 19]，这是跨孤岛 FL 的固有问题，使其难以在实践中部署。一方面，数据以不平衡的方式分布在客户端（称为统计异质性），这往往会导致本地模型的差异，并对收敛行为产生不利影响。这样，就需要执行额外的加密通信，从而影响 FL 的训练效率。另一方面，客户端的计算能力和通信带宽可能各不相同（称为系统异质性）。这就导致了一个突出的落后问题，而计算密集型的加密/解密操作又会进一步加剧这一问题，从而大大减慢训练进度。如果不解决客户端异构问题，就无法充分发挥 PHE 的威力。

我们将我们的主要贡献总结如下：

我们提出了 FedPHE，这是一种高效、抗落后的异构客户端同态加密 FL 框架。据我们所知，这是 首次尝试实现安全客户端选择和加权聚合，以有效解决客户端异构性带来的挑战，从而缩小隐私保护 FL 与实际应用之间的差距。
在 CKKS 的同态加密基础上，FedPHE 实现了高效的加密加权聚合，考虑到了局部更新对全局模型的贡献。为了优化数据传输效率，FedPHE 采用了数据包级稀疏化方法，解决了使用普通 CKKS 密文大小增加的问题。
FedPHE 利用本地更新的草图，以保护隐私的方式促进通信效率高的客户端选择。通过联合考虑数据分布和资源可用性，FedPHE 将类似的客户端聚类在一起，然后从每个聚类中挑选速度最快的客户端，从而在不影响模型准确性的情况下有效缓解了落后问题。
在真实数据集上的大量实验表明，与最先进的方法相比，FedPHE将训练速度提高了1.85 − 4.44×，将通信开销降低了1.24 − 22.62×，并将散兵游勇效应减轻了1.71 − 2.39×，模型精度略有下降（仅为1.58%）。

预备知识和动机

预备知识

流行的 HE 方案包括 Paillier [27]、BFV [28] 和 CKKS [29]，其中 Paillier 只允许对密文进行加法运算，而 BFV 和 CKKS 则同时支持加法和乘法运算。其中 BFV 仅支持整数运算， CKKS 支持实数运算。

动机

对密文进行加权聚合的必要性
简单地进行非加权汇总会导致全局模型出现不理想的偏差，从而阻碍训练的收敛性。更合适的方法是进行加权聚合，即根据客户的贡献（如数据大小或质量）分配不同的聚合权重，例如联邦平均算法根据数据量来进行加权聚合。
高效加密聚合的必要性
抵抗落后问题的必要性
选择客户端的必要性

FedPHE 的设计

总览

具体来说，应实现以下理想目标：

隐私保护。在聚合过程中应保护客户端的隐私。也就是说，PS 不能泄露任何与单个客户端有关的敏感信息，而客户端也不能访问他人的任何隐私数据。我们假设 HE 密钥对通过安全通道在客户端之间共享，并且 PS 不会与任何客户端串通 [14, 33]。
效率。由于高计算量和通信开销使得 HE 难以在实践中实现，因此我们希望它能在每一轮加密和传输本地模型时提高效率。
抗落后效应。在客户端异质性的情况下，它应能有效减轻落后者的负面影响，在不影响模型准确性的前提下加快训练过程。

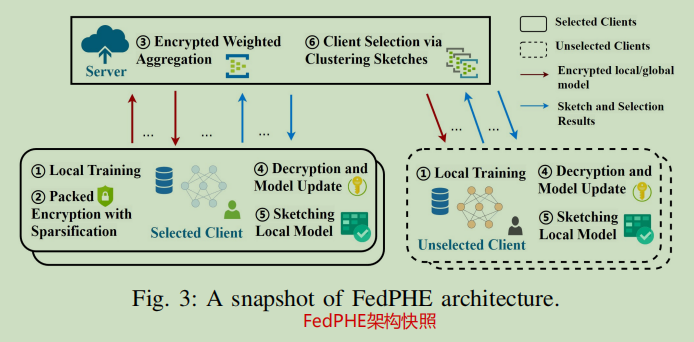
FedPHE 的通信轮次如下步骤所述（示意图见图3）：

本地训练。在每一轮 \(t\) 开始时，每个客户端 \(i\in N\) 都会按照公式（2）运行 \(E\) 步本地随机梯度下降，以计算本地模型 \(w_i^t\)；
带稀疏化的打包加密。任何选定的客户端 \(i\in \mathcal{S}^t\) 都会将本地模型 \(w_i^t\) 扁平化并打包成 \(\{\mathcal{P}_i^1, \cdots ,\mathcal{P}_i^K\}\)，然后在包粒度上执行稀疏化；之后，它会对稀疏打包的本地模型进行加密，最后将密文 \(C_i^t\) 和掩码 \(M_i^t\) 发送给 PS 进行聚合；
加密加权聚合。PS 将收到的加密本地模型与加密权重聚合在一起，然后计算新的加密全局模型 \(C^t\) 和掩码 \(M^t\) 并发送给所有客户端；
解密和模型更新。每个客户端对全局密文进行解密和解包，以获得全局模型 \(w^t\)，然后更新本地模型 \(w^t_{i,0} = w^t\)；
绘制本地模型草图。然后，每个客户端 \(i\in N\) 计算并向 PS 发送本地模型 \(h^t_i\) 的草图；
通过聚类草图选择客户端。PS 从 \(N\) 个客户端中选择一个子集 \(S^{t+1}\) 作为参与方，并根据其贡献得出聚合权重 \(p^{t+1}_i\)。

在每个全局回合 \(t\) 中，只有选定的客户端执行 PHE 和稀疏化，然后将加密的模型更新和掩码（第 14-16 行）传输给 PS，但需要注意的是所有客户端都需要上传模型草图。根据客户端的贡献，PS 进行加密加权聚合，并将结果发送给所有客户端（第 3-5 行）。解密和模型更新后，客户端将其本地模型草图发送给PS（根据草图选择下一轮参与的客户端和权重）（第 17-19 行）。然后，PS 会选择一个客户端子集作为下一轮的参与者 \(\mathcal{S}^{t+1}\)（第 6-8 行）。

FedPHE算法细节如下：

贡献感知加密加权聚合

为适应客户端的异质性，聚合权重根据局部更新对全局模型的贡献进行调整，如算法2。

基于CKKS的PHE

一方面，CKKS 可以直接在向量上对实数进行加密，而 Paillier 和 BFV 将整数作为输入明文，这就需要对浮点数进行量化。这提升了加密和解密操作的效率。另一方面，CKKS 支持同态乘法，因此适合在异构跨孤岛 FL 下实现安全的加权聚合。相比之下，Paillier 只支持同态加法，而 BFV 在加密后对量化整数进行乘法运算时可能会遇到溢出问题。
注意：服务器的权重也是加密的。客户端上传的参数也是加密的。因此使用乘法同态可以直接把加密权重和加密参数乘起来。

包级稀疏化

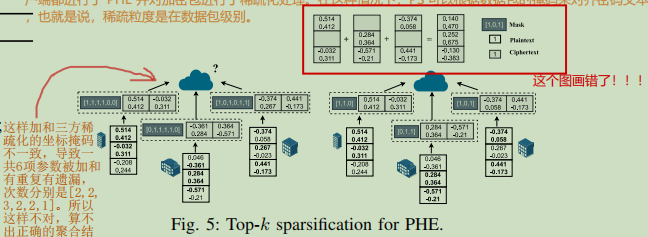
在这种情况下，PS 可以根据数据包的掩码对密文进行对齐，也就是说，稀疏性粒度是在数据包层面上的。稀疏化率s%是提前给定的，依此来计算掩码。
需要注意的是：在异构场景中，客户端的模型更新是本地加权的，这种针对 CKKS 的稀疏化技术同样可以进一步应用于提高 Paillier 和BFV 的效率。

贡献感知加权聚合

为适应客户端的异质性，PS 会将选定客户端的加密本地更新聚合在一起，并根据其对全局模型的贡献进行加密加权。客户端 \(i\) 的贡献是使用这一轮的草图和上一轮草图的相似度（碰撞概率）衡量的。
局部敏感哈希（LSH）[35]已被广泛用于许多应用中，以近似Jaccard相似性。根据 [36] 的观点，较低的相似度意味着较高的推理损失，可能会取得更好的性能提升。
注意：服务器负责计算被选中客户端的权重。数据在服务器是加密的，所以服务器是使用LSH近似计算JS，因此算法2 的权重计算实际上需要全部客户端提前上传草图（通过LSH进行哈希）。

\[\Pr_{\mathcal{H}}(h_{i}^{t-1}=h_{i}^{t})=JS(w_{i}^{t-1},w_{i}^{t}),\tag{4} \]

\[p_i^t=\frac{\exp(-\beta\cdot JS(w_i^{t-1},w_i^t))}{\sum_{j\in\mathcal{S}^t}\exp(-\beta\cdot JS(w_j^{t-1},w_j^t))}.\tag{5} \]

其中\(\beta\)是一个正数，用于修正指数函数的曲线。

从选定的客户端 \(\mathcal{S}^t\) 处接收密文 \(\{C^t_1 , \cdots , C^t_{\mathcal{S}_t} \}\) 和掩码 \(\{M^t_1 , \cdots , M^t_{\mathcal{S}_t}\}\) 后，PS 执行加密加权聚合以获得全局模型，即

\[\boldsymbol{E}(\boldsymbol{w}^{t+1})=\sum_{i\in\mathcal{S}^t}\boldsymbol{E}\left(p_i^t\right)\times\boldsymbol{E}\left(\boldsymbol{w}_i^t\right),\tag{6} \]

其中 \(E(p^t_i)\) 表示分配给客户端 \(i\) 的加密权重。基于 CKKS 的同态乘法，方程(6) 中的这种聚合相当于对明文进行加权聚合，然后对结果进行加密，即

\[\boldsymbol{E}(\boldsymbol{w}^{t+1})=\sum_{i\in\mathcal{S}^t}\boldsymbol{E}\left(p_i^t\times\boldsymbol{w}_i^t\right).\tag{7} \]

加密后的全局模型 \(\mathcal{C}^t\) 和掩码 \(\mathcal{M}^t\) 随后会分发回所有客户端进行解密和模型更新。我们在算法2 中总结了 FedPHE 如何进行贡献意识加密加权聚合。

基于草图的客户端选择

问题：不同客户端可能发送相似或相关的模型更新给服务器，这会导致不必要的通信开销。
具体来说，在每一轮中，客户端计算并向 PS 传输模型更新的草图，然后PS 将相似的草图聚类，并从每个聚类中选择速度最快的客户端。主要步骤总结如算法3 所示。

对每个客户端的展平参数求局部敏感度哈希

具体而言，LSH 是函数 \(\mathcal{F}\) 的一个族 \(\mathcal{H}\colon\mathbb{R}^d\to\mathbb{S}\)，其特性是如果两个输入在原始数据空间中相似，那么经过哈希转换后也会有很高的相似度。我们利用 LSH 函数的特性，在两个输入具有相同哈希代码的情况下，在碰撞过程中表示输入有更高的相似性。

对所有草图聚类

先计算出最佳的聚类数量再对客户端的更新进行聚类，聚类数是动态变化的，但最高不会超过提前设定的阈值。

可以通过 K-means 将客户端聚类为 \(C\) 个类别 \(\{\mathcal{A}^t_1 ,\cdots, \mathcal{A}^t_\mathcal{C}\}\)，其中同一类别中的客户端具有相似的草图。而有相似的草图意味着本地模型相似。那么服务器从每个聚类中选择一个客户端，这样所有参与的客户端就的本地更新都不相似，这样就减少了不必要的通信开销。此外，从每个聚类中选择客户端不是随机选的，而是要保证效率，选择历史上上传最快的（根据历史上服务器接收到该客户端上传参数的次序确定该客户端被选择的优先级，最终选择每个聚类中优先级最高的客户端）。

安全性分析

在本文中，我们 假定 PS 不会与任何客户端串通，PS 和客户端都是诚实但好奇的，这是 FL 文献中广泛采用的威胁模型 [40]。

定理 1. 诚实但好奇的服务器无法推断出客户端的任何隐私信息。
证明. 在提议的 FedPHE 中，由于接收到的本地更新在传输前已加密，因此 PS 只能访问密文。因此，PS 无法推断客户端的数据和本地模型。

定理 2. 诚实但好奇的客户端无法窃听他人的任何隐私信息。
证明. FedPHE 开始时，PS 和客户端会建立安全的 HTTPS 连接，使用 TLS/SSL 协议对传输的数据进行加密，确保攻击者无法访问数据。

定理 3. 通信中传输的草图和掩码不会泄露客户端的隐私。
证明. 在 LSH 中，矩阵 \(\mathcal{M}\) 由秘密共享种子 \(s\) 生成，用于将参数映射为加密形式。掩码暗示的是一个包，而不是一个标量，不会泄露隐私。攻击者不知道种子 \(s\)，只能通过猜测来推断矩阵 \(\mathcal{M}\)。

实验

实验设置（平台和参数）

使用 Pytorch 在配备 NVIDIA GeForce RTX 3060 Ti GPU 的戴尔服务器上进行评估。考虑跨孤岛 FL 场景，其中 \(N = 8\) 个客户端协同训练一个模型。我们研究了 Dirichlet Non-IID 数据设置（\(\alpha = 1\)）的客户端异质性，与 [41] 类似。我们使用 TenSEAL [42] 实现了 BFV 和 CKKS，并将它们的多模度设置为 \(8192\)。为了模拟落后者的存在，我们随机选择 \(25\%\) 的客户端作为落后者，并引入 \(2\sim 5\) 轮训练时间的人为延迟。批量大小为 \(B = 64\)，学习率为 \(\eta = 10^{-3}\)。LSH 哈希函数的数量为 \(k = 200\)。

数据集和模型

我们在三个真实数据集上对结果进行了评估：MNIST [43]、FashionMNIST [44] 和 CIFAR- 10 [45]。其中，我们将 MNIST 和 FashionMNIST 分成 60,000 个训练数据和 10,000 个测试数据。对于 CIFAR- 10，我们分别使用 50,000 和 10,000 幅图像作为训练数据和测试样本。MNIST 采用了直接的 LeNet-5 神经网络架构[43]。对于 FashionMNIST，我们使用了一个包含 2 个卷积层和 1 个全连接层的 CNN 模型。在 CIFAR-10 数据集上的实验采用了 ResNet-20 模型[46]。

Baseline

为了验证所提出的FedPHE，我们引入了以下联邦学习算法进行比较。

明文：计算和通信开销的理想上限，参数传输和加权聚合在明文中进行。
BatchCrypt：基于 Paillier 的 PHE [14]，客户端首先量化，然后打包和加密模型更新，而 PS 对密文进行聚合。
PackedBFV：基于 BFV 的 PHE [28]，由于 BFV 仅支持整数运算，因此在加密之前，还需要对模型更新进行量化和加权。
PackedCKKS：基于CKKS的PHE[29]，利用CKKS的密文乘法，促进PS端的加密加权聚合。
FedAvg：联邦平均 [31]，其中 PS 随机选择客户端子集进行聚合。
FLANP：具有自适应客户端参与的落后弹性 FL [47]，它从较快的客户端开始训练过程，并在达到当前参与者数据的准确性后逐渐包括较慢的客户端。