Federated Learning with Differential Privacy：Algorithms and Performance Analysis

2024/2/11
大四做毕设的时候第一次读这篇论文，当时只读了前一部分，后面关于收敛界推导证明的部分没有看，现在重新完整阅读一下这篇文章。

本文贡献

1. 提出了一种基于差分隐私 (DP) 概念的新框架，其中在聚合之前将人工噪声添加到客户端的参数中，即模型聚合前加噪FL (NbAFL)
2. 我们提出了 NbAFL 中经过训练的 FL 模型的损失函数的理论收敛界限。并且发现了这个理论这个理论界限的三个关键性质：
   1. 收敛性能和隐私保护级别之间存在折衷，即更好的收敛性能导致更低的保护级别；
   2. 给定固定的隐私保护级别，增加参与FL的整体客户端数量\(N\)可以提高收敛性能；
   3. 就给定保护级别的收敛性能而言，存在最大聚合次数（通信轮次）的最佳数目。
3. 提出了一种 \(K\) 随机调度策略，即每轮次全局聚合从全局的 \(N\) 个客户端中随机选择 \(K(1<K<N)\) 个客户端来参与聚合。我们还发现了这种情况下损失函数的相应收敛界，并且 \(K\) 随机调度策略也可以保留上述三个属性。此外，我们发现存在一个最优 \(K\)，可以在固定隐私级别下实现最佳收敛性能。

创新点

1. 到目前为止，现有文献中尚未详细介绍具有隐私保护噪声扰动的 FL 收敛行为的理论分析，这将是本文工作的主要重点。
2. 为了有效防止信息泄漏，我们提出了一种基于差分隐私（DP）概念的新框架，其中每个客户端在将其上传到服务器进行聚合之前故意添加噪声来扰乱其训练参数，即：模型聚合 FL 之前添加噪声(NbAFL)。
3. 在理论上发现了添加人工高斯噪声的 NbAFL 中经过训练的 FL 模型的损失函数的收敛边界。

威胁模型

1. 本文中的服务器被假定为诚实的。然而，有外部敌手觊觎客户端的隐私信息。
2. 尽管第 \(i\) 个客户端的个人数据集 \(D_i\) 保存在客户端本地，但中间参数 \(w_i\) 需要与服务器共享，这可能会泄露客户端的隐私信息，比如通过模型逆向攻击。
3. 此外，我们还假设上行链路信道比下行链路广播信道更安全，因为客户端可以在每个上传时间动态分配到不同的信道（例如，时隙，频带），而下行链路信道是广播的方式。因此，我们假设上行链路中每个客户端上传的参数最多有 \(L(L\leq T)\) 次曝光（这是因为每一轮通信不是每个客户端都被选中，只有被选中的需要上传参数），下行链路中聚合参数最多有 \(T\) 次曝光，其中 \(T\) 是聚合次数。

预备知识

\((\epsilon,\delta)\)差分隐私

对于随机机制\(\mathcal{M}\)，相邻数据集\(\mathcal{D}_i\)、\(\mathcal{D}_i^{\prime}\)，输出集合\(\mathcal{S}\)满足：

\[\Pr[\mathcal{M}(\mathcal{D}_i)\in\mathcal{S}]\leq e^\epsilon\mathrm{Pr}[\mathcal{M}(\mathcal{D}_i^{\prime})\in\mathcal{S}]+\delta. \]

满足\((\epsilon,\delta)\)差分隐私的高斯噪声\(n\sim N(0,\sigma^2)\) ，从高斯分布中采样噪声，其中 \(\sigma \geq c\Delta s/\epsilon\)（其中\(\Delta s=\max\|s(\mathcal{D_i})-s(\mathcal{D_i^{\prime}})\|\)，\(s\)是一个实值函数），\(c \geq \sqrt{2ln(1.25/\delta)}\)。
也就是采样的高斯分布的标准差\(\sigma\)满足：\(\sigma\geq\frac{\sqrt{2ln(1.25/\delta)}\Delta s}{\epsilon}\)

符号表

差分隐私保护的联邦学习

全局差分隐私

对于上行链路的全局差分隐私

\[s_\mathbf{U}^{\mathcal{D}_i}\triangleq\mathbf{w}_i=\arg\min_\mathbf{w}F_i(\mathbf{w},\mathcal{D}_i)=\frac1{|\mathcal{D}_i|}\sum_{j=1}^{|\mathcal{D}_i|}\arg\min_\mathbf{w}F_i(\mathbf{w},\mathcal{D}_{i,j}) \]

（这里下标\(U\)指的是上行链路的意思）

\[\Delta s_\mathrm{U}\triangleq\max\left\{\Delta s_\mathrm{U}^{\mathcal{D}_i}\right\},\quad\forall i \]

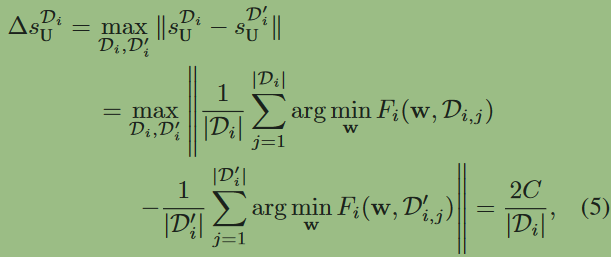
假设最小的本地数据集大小为\(m\)，那么可以得到\(\Delta s_\mathrm{U}=\frac{2C}{m}\)，那么要让上行链路每次曝光满足\((\epsilon,\delta)\)差分隐私，需要使\(\sigma_{\mathbf{U}}=c\Delta s_{\mathbf{U}}/\epsilon\)，那么考虑到本地数据集\(L\)次曝光，因此每次添加的噪声\(\sigma_{\mathbf{U}}=\frac{c\Delta s_{\mathbf{U}}}{\epsilon/L}=\sigma_\mathbf{U}=cL\Delta s_\mathbf{U}/\epsilon\)(总的隐私预算是\(\epsilon\)，那每次曝光的隐私预算是\(\epsilon/L\))

对于下行链路的全局差分隐私

从下行链路角度来看，\(\mathcal{D}_i\)的聚合操作可以表示为

\[s_\mathrm{D}^{\mathcal{D}_i}\stackrel{\Delta}{=}\mathrm{w}=p_1\mathrm{w}_1+\ldots+p_i\mathrm{w}_i+\ldots+p_N\mathrm{w}_N, 1\leq i\leq N \]

此处，\(p_i\)是联邦聚合时每个客户端的权重。

引理一
聚合后数据集\(\mathcal{D}_i\)的敏感度\(\Delta s_\mathrm{D}^{\mathcal{D}_i}\)为：

\[\Delta s_\mathrm{D}^{\mathcal{D}_i}=\frac{2Cp_i}m. \]

备注1：根据引理一，要达到下行链路一个小的全局敏感度

\[\Delta s_\mathrm{D}\triangleq\max\left\{\Delta s_\mathrm{D}^{\mathcal{D}_i}\right\}=\max\left\{\frac{2Cp_i}m\right\},\quad\forall i. \]

为了让这一项最小，那么即找到最小的 \(\max{p_i}\)，又因为所有 \(p_i\) 加和等于 \(1\)，那么理想的条件就是所有客户端使用相同大小的本地数据集训练 \(p_i=1/N\).

聚合后加噪的联邦学习算法

其中\(\frac{\mu \|w_i-w_{(t-1)}\|^2}{2}\)是修正项，是FedProx框架提出并引入的项，为了降低数据异质性带来的影响，提高整体框架的稳定性。该修正项的本质是针对局部模型中的参数和全局模型中的参数增加差异性的限制，从而为解释全局与部分局部信息之间的异质性提供理论依据。
MLSys提前看｜机器学习的分布式优化方法