【练习回顾】第六章 数据结构基础
E6-1 并行程序模拟 Concurrency_Simulator UVa210
1.typedef层层封装,struct模拟了"程序"(Program),"语句"(Statement);程序队列使用了deque<Program> Rq,阻止队列使用了queue<Program> Lq,程序中语句命令序列使用了queue<Statement> seq。
各种东西引用叠在一起挺眼花的。
2.虽说分了readInProgram()、runProgram()、runInQuantum()。但都是在主体中写完一段逻辑后感觉太长,将其分出的。有点挤牙膏,但最后观感还可以,还便于debug。这种写法流程似乎可以借鉴。
·runInQuantum()仅仅包装了一个较大的for循环,逻辑上刚好是执行Qt单位配额。变量域也变得很清爽
3.运行时出现报错std::bad_alloc:
原因在于执行Lq.front()和Lq.pop()前未判断是否为空,以致Rq.push_front(Lq.front())时地址分配出错
E6-2 Rails UVa514
经典的判断:对于缓冲区已有输入,通过一个栈,可否给出目标输出。
好像没法总结出小结论呐,标准的模拟法:
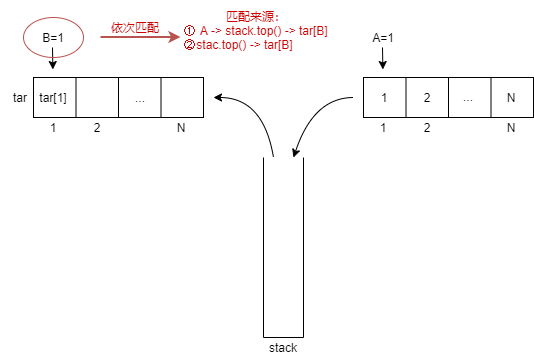
int A=1,B=1;
bool isok=1;
while(B<=N){
if(tar[B]==A){++A;++B;}
else if(!s.empty() && s.top()==tar[B]) {s.pop();++B;}
else if(A<=N) s.push(A++);
else { isok=0;break; }
}
printf("%s\n",isok ? "Yes" : "No");
E6-3 矩阵链乘Matrix Chain Multiplication UVa442
1.用stack<int>栈记录表达式:考虑清楚“括号”是否需要入栈,还是只需读取时作为运算操作的检测标志。
题目中的输入:两个矩阵必有括号辅助运算,所以遇到')'直接合并栈顶两个矩阵即可,不用多想。
理解题意:第三行两个Expression就是指两个矩阵

E6-4 破损键盘Broken Keyboard UVa11988
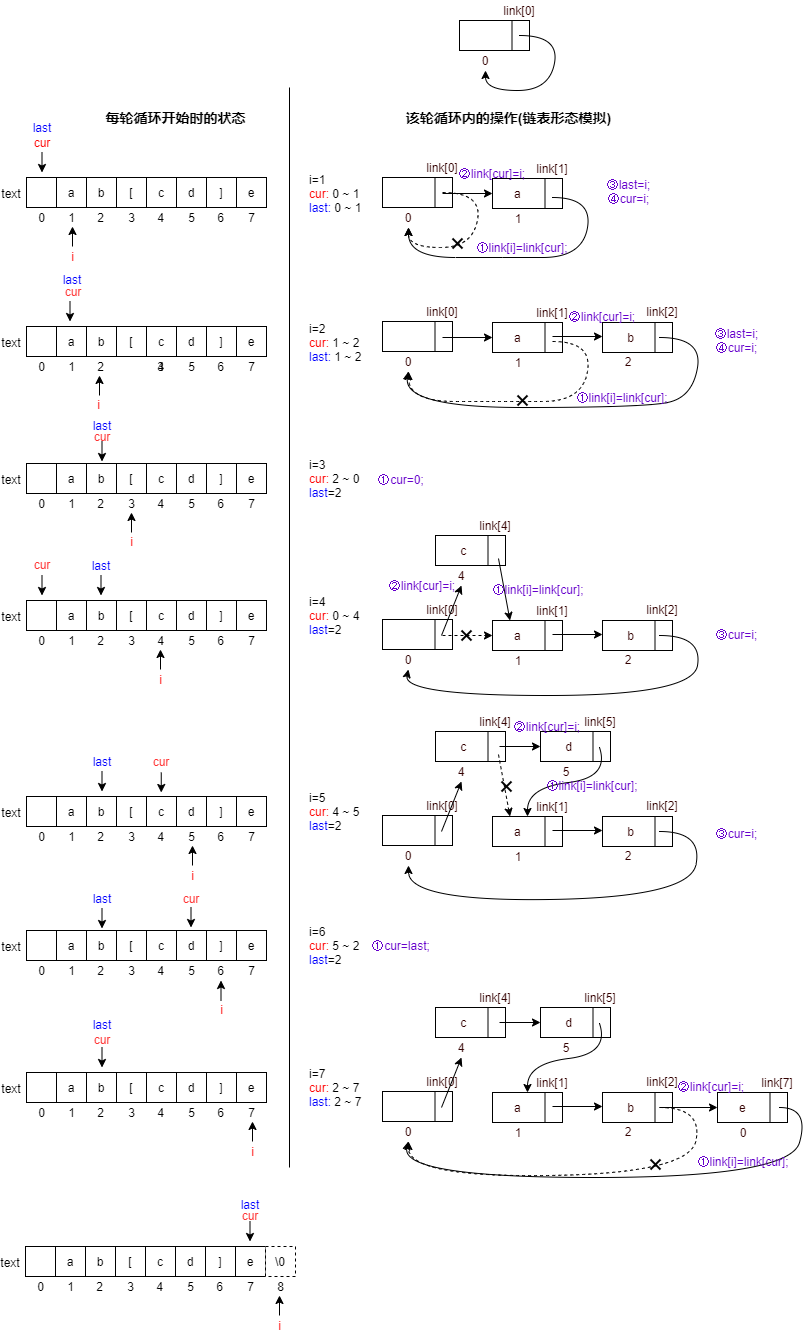
典型的链表插入操作。然而内容只是字符,不妨只添加一个数组当作链表指针,字符数组的下标即为内容地址。数组型的链表运算速度和存储空间都有极大优化,但也容易糊掉(笨死了!);同时为了将不同操作整合在一个循环种,代码个中逻辑想了半天(火大!)
#include<cstdio>
#include<cstring>
#define MAXN 100007
char text[MAXN];
int link[MAXN]; //用数组而不用指针,方便高效
const int HEAD=0; //索引下标即为地址
int main(){
while(scanf("%s",text+1)==1){
int cur=HEAD;
int last=HEAD;
link[cur]=HEAD; //链表初始化
for(int i=1;text[i];++i){
if(text[i]=='[') cur=0;
else if(text[i]==']') cur=last;
else {
link[i]=link[cur];
link[cur]=i;
if(cur==last) last=i;
cur=i;
}
}
for(int i=link[HEAD];i!=HEAD;i=link[i])
printf("%c",text[i]);
puts("");
}
return 0;
}
说明:
| 含义 | 数组链表 | 指针链表 |
|---|---|---|
| 某一个链表的地址 | (int)i | (Type*)p |
| 地址i处 表的内容 | text[i] | p->text |
| 地址i处 表的指针 | link[i] | p->link |
这里的i其实相当于以往用的p,指向当前待链入表地址(下标);
这里的cur其实相当于以往用的pre,指向准备向后链入的表地址(下标);
主要操作:
link[i]=link[cur];//将待链入表i的指针指向头,形成闭环
link[cur]=i; //将表cur的指针指向i,将i链入
if(cur==last) last=i; // 若cur和last指向同处,说明未返回home,则和cur一起更新位置
cur=i //更新cur的位置
报错crosses initialization of
多发在switch中定义变量。变量的作用域在花括号间,倘在某case后定义变量,其作用域会持续到switch结束;若该case被跳过,则变量未定义,可能会出错,因而报错。
解决方法:该case间用花括号括起来,规定作用域。
E6-5 移动盒子Boxes in a Line UVa12657
复杂的链式结构容易出毛病,一般问题出在:
①修改某指针指向后的产生隐式牵连;
②多情况操作杂糅产生错误(链表头尾、相邻与否);
③地址合法判断。
此题考查链表元素的移动,为了简化逆序排列的操作,采用的双向链表和标记isrvs。
1.双向链表链接操作封装:
void link(int L,int R) {rlink[L]=R;llink[R]=L;}
//注意:修改了L的rlink和R的llink
2.考量①,顺序相关:
· 将x插到y左侧:先将x取出,两端链合 link(llink[y],x); link(x,y);
· 将x插到y右侧:先将x取出,两端链合 link(y,x); link(x,rlink[y]);
· 将x与y换位置:此时不能像前两个一般,对所有位置适用了,分两种情况:
xy毗邻:-
if(rlink[x]==y)link(lx,y);link(y,x);link(x,ry);
-
if(rlink[x]==y)link(lx,y);link(y,x);link(x,ry);
xy相隔:-
link(lx,y);link(y,rx);link(ly,x);link(x,ry);
其中lx,rx,ly,ry
3.考量②,在操作复杂的时候(像双向链表),不妨直接存下需要修改链接的地址,直接表示而非类似rlink[x]等间接表示。此时顺序便无关紧要了。在上一条xy换位时,便是如此事先声明:
int lx=llink[x],rx=rlink[x];
int ly=llink[y],ry=rlink[y];
4.考量③,合法内容是{1,2,...N},便添加 {0,N+1}作为头和尾,同时使llink[0]=-1,rlink[N+1]=-1,即可在输出奇数位链表时所有地址情况均对for合法适用
E6-6 小球下落Dropping Balls UVa679
满二叉树FBT,数组形式(实现方式也为数组)
1.一些习惯
最大深度为D:int tr[1<<D]; 结点数(1<<D)-1
从1开始编号:k*2 k*2+1 k/2
从0开始编号: k*2+1 k*2+2 (k-1)/2
2.关于此题:要开始有估算运行效率的习惯了,而不是死用数据结构。第I个球的落点信息已经包含在I中,不需要通过模拟1~I的过程
int node=1;
for(int layer=1;layer<D;++layer){
if(I&1) { node*=2; I=(I+1)/2; }
else { node=node*2+1; I=I/2; }
}
printf("%d\n",node);
E6-7 树的层次遍历Trees on the level UVa122
限制条件是结点数256,那么考虑到极端树型,应使用指针形式(实现方式倒是既可以用指针也可以用数组),否则开\(2^{256} \approx 1.1 \times 10^{77}\)个数组谁顶得住。
1.C++式结构声明:加强了struct,趋向于class
struct Node{
Node *lchild,*rchild;
int val;
bool init;
Node():lchild(NULL),rchild(NULL),val(0),init(false){};
//C++构造函数列表初始化
};
Node* root;
E6-8 Tree Uva548
递归很好的解决了因不断下分子树而产生的记忆存储问题
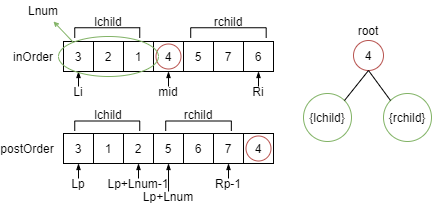
1.通过中序+后序遍历求二叉树:递归的写法,完全应用树递归式的定义
int inOrder[maxn],postOrder[maxn],n;
int lchild[maxn],rchild[maxn];
int buildTree(int Li,int Ri,int Lp,int Rp){//i:inOrder p:postOrder
if(Li > Ri) return 0;
int root = postOrder[Rp];
int mid;
for(mid=Li;inOrder[mid]!=root;++mid);
int Lnum = mid - Li;
lchild[root] = buildTree(Li,mid-1,Lp,Lp+Lnum-1);
rchild[root] = buildTree(mid+1,Ri,Lp+Lnum,Rp-1);
return root;
}
2.dfs计算权值和
void dfsFind(int u,int sum){
sum += u; //加上当前根节点权值
if(!lchild[u] && !rchild[u]){ //遇到叶结点,计算最终结果,结束这一程序分支
if(sum < Wmin || sum == Wmin && u < Nmin){
Nmin = u;
Wmin = sum;
}
}
//没遇到叶结点,向左右子树分支
if(lchild[u]) dfsFind(lchild[u],sum);
if(rchild[u]) dfsFind(rchild[u],sum);
}

