Longest Palindromic Substring

Longest Palindromic Substring

---

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.
Example 2:

Input: "cbbd"
Output: "bb"

---

在学习动态规划时刷到的一道题，题目求的是给定字符串中最长的回文字符串序列，算是非常经典的一道题了。本题有许多解法，在此只列举两种。

1. 动态规划

既然其在LeetCode属于动态规划题目，自然免不了动态规划的方法，首先定义一个bool二维数组dp[i][j]代表的是从第i个字符到第j个字符之间的字符串是否是回文字符串，自然状态方程很容易得到如下：

 

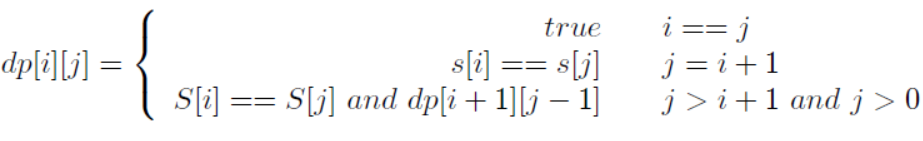
 对应代码如下：

class Solution {
public:
    string longestPalindrome(string s) {
        if(s.length() < 2) return s;
        int max_len = 0;
        string max_len_str = "";
        vector<vector<int>> dp(s.length(), vector<int>(s.length()));
        
        for(int j = 0; j < s.length(); j++){
            dp[j][j] = 1;
            if(max_len == 0) {max_len = 1; max_len_str = s.substr(j, 1);} // case 1 
            for(int i = 0; i < j; i++){
                if(s[i] == s[j] && (j - i < 2 || (j > 0 && dp[i + 1][j - 1] == 1))){ // case 2 and 3
                    dp[i][j] = 1;
                    if(dp[i][j] == 1 && j - i + 1 > max_len){
                        max_len = j - i + 1;
                        max_len_str = s.substr(i, j - i + 1);
                    }
                }
            }
        }
        return max_len_str;
    }
};

2. 中心扩展算法　

class Solution {
public:
    string center_expand(string s, int left, int right){
        while(left >= 0 && right < s.length() && s[left] == s[right]){
            left--; right++;
        }
        return s.substr(left + 1, right - left - 1);
    }
    string longestPalindrome(string s) {
        if(s.length() < 2) return s;
        string max_len_str = "", tmp_even_str = "", tmp_odd_str = "";
        for(int i = 0; i < s.length(); i++){
            tmp_even_str = center_expand(s, i, i + 1);
            tmp_odd_str = center_expand(s, i, i);
            if(tmp_odd_str.length() > max_len_str.length()) max_len_str = tmp_odd_str;
            if(tmp_even_str.length() > max_len_str.length()) max_len_str = tmp_even_str;
        }
        return max_len_str;
    }
};