题解：AT_diverta2019_f Edge Ordering

图是借用官方题解的。考虑钦定一个最小生成树的加边顺序。

黑色边是一颗生成树。对于 \(7\) 号边，对他最紧的限制是其权值一定大于 \(3\) 号边。对每一条限制连有向边，那么最后形成的一定是一个拓扑图。

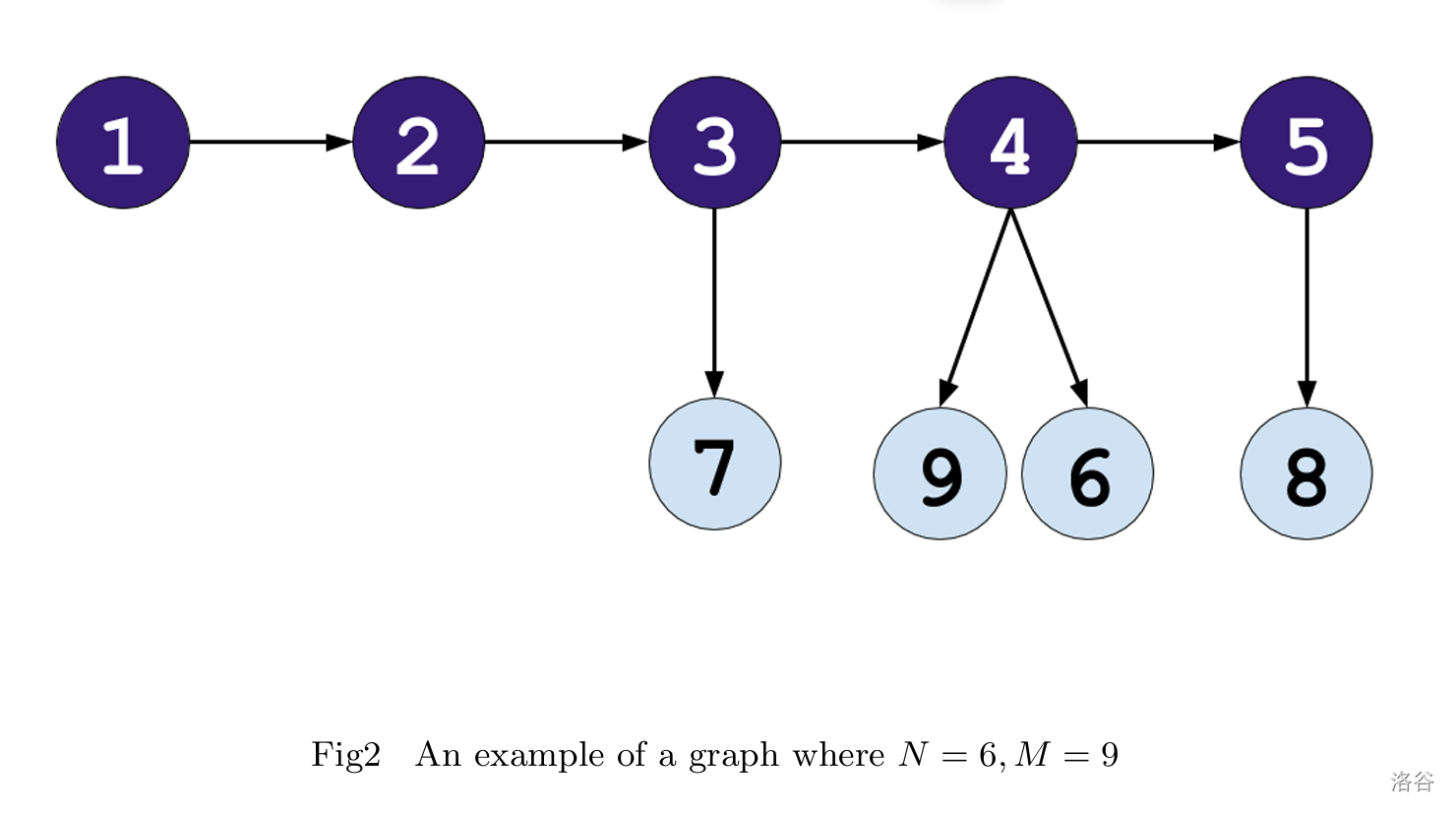
考虑算他的贡献，从后往前加边，先加非树边再加树边，例如以上这个图的加边顺序为 \(\text{8,5,6,9,4,7,3,2,1}\)。钦定了这样的顺序后，非树边可以任意选择权值，而树边只能成为当前序列的最小值。

用四元组 \((n,b,c,s)\) 描述现在的状态，意义为有 \(n\) 条边，\(b\) 条树边，这样的方案数为 \(c\)，当前的总贡献和是 \(s\)。

对于转移，加入一条非树边：\((n,b,c,s)\rightarrow (n+1,b,(n+1)c,(n+2)s)\)。加入若干条非树边的代价易于计算。

加入一条树边：\((n,b,c,s)\rightarrow(n+1,b+1,c,s+(b+1)c)\)。这样你得到了一个 \(O(n!)\) 算法。

易于发现一条非树边对应了生成树的一条路径，这条非树边一定在这条路径上的树边以后加入。于是考虑设 \(f_S\) 为集合为 \(S\) 的树边固定后的四元组。枚举新加入的边即可。发现需要维护一个边集对应的非树边数，这个东西可以先搜出来后做一遍高维前缀和。复杂度即为 \(O(n2^n)\)。

#include<iostream>
#include<vector>
const int N = 500, p = 1e9 + 7;
std::vector<std::pair<int, int>> g[N];
int n, m, s, rs, f[1<<21][4], h[1<<21], fc[N], iv[N], a[N], b[N];
int qp(int a, int b){int r = 1;
    for(; b; b >>= 1, a = 1ll * a * a % p)
        if(b & 1) r = 1ll * r * a % p; return r;
}
void dfs(int x, int y, int fa, int d){
    if(x == y) return ++h[s - d], void();
    for(auto [v, w] : g[x]) if(v != fa) dfs(v, y, x, d | (1 << w));
}
int main(){
    std::cin >> n >> m; fc[0] = iv[0] = 1;
    for(int i = 1; i < N; i++)
        fc[i] = 1ll * fc[i - 1] * i % p,
        iv[i] = qp(fc[i], p - 2);
    for(int i = 1, x, y; i < n; i++)
        std::cin >> x >> y, a[i] = x, b[i] = y,
        g[x].push_back({y, i - 1}), g[y].push_back({x, i - 1});
    s = (1 << n - 1) - 1;
    for(int i = n, x, y; i <= m; i++)
        std::cin >> x >> y, dfs(x, y, 0, 0);
    for(int i = 0; i < n; i++) for(int j = (1<<n-1)-1; ~j; j--)
        if(!(j & (1 << i))) (h[j] += h[j ^ (1 << i)]) %= p;
    f[0][0] = f[0][1] = f[0][3] = 0, f[0][2] = 1;
    for(int i = 1; i <= s; i++){
        f[i][1] = __builtin_popcount(i);
        f[i][0] = f[i][1] + m - n + 1 - h[i];
        int x = i; while(x){
            int u = x & -x, v = i ^ u, l = h[v] - h[i]; x ^= u;
            (f[i][2]+=1ll*f[v][2]*iv[f[v][0]]%p*fc[f[v][0]+l]%p)%=p;
            (f[i][3]+=1ll*f[v][3]*iv[f[v][0]+1]%p*fc[f[v][0]+1+l]%p)%=p;
        } (f[i][3] += 1ll * f[i][1] * f[i][2] % p) %= p;
    } std::cout << f[s][3];
}