P6718 [CCO2018] Flop Sorting

给定长为 \(n\) 的序列 \(a\)，一次操作可以指定 \(l,r\)，将 \(a_l,a_{l+1}\cdots a_r\) 中最大值与最小值调换位置，在 \(q\) 次操作以内将 \(a\) 变为另一指定序列。

首先要发现这个东西是可逆的，意思是做两次相同的操作不会改变这个序列。也即：如果一个序列经过若干次操作后达到一个状态，将操作序列翻转可以还原到原序列。

于是考虑找到一种操作方式将原序列排序，就解决了这个问题。

至于排序方法，考虑进行一个类似归并的分治。问题在于如何合并两个已经有序的序列。

如果有两个不相交的序列，可以用这种方式来排序：先将两个序列各自翻转，拼接成为一个下降序列，然后翻转回来。代价是 \(O(n)\)。

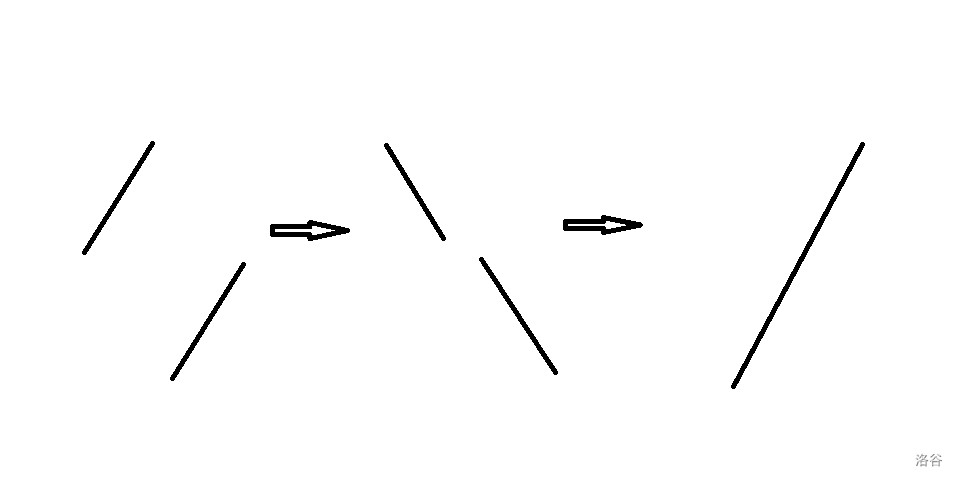
于是就可以对值域分治，过程形如这样：

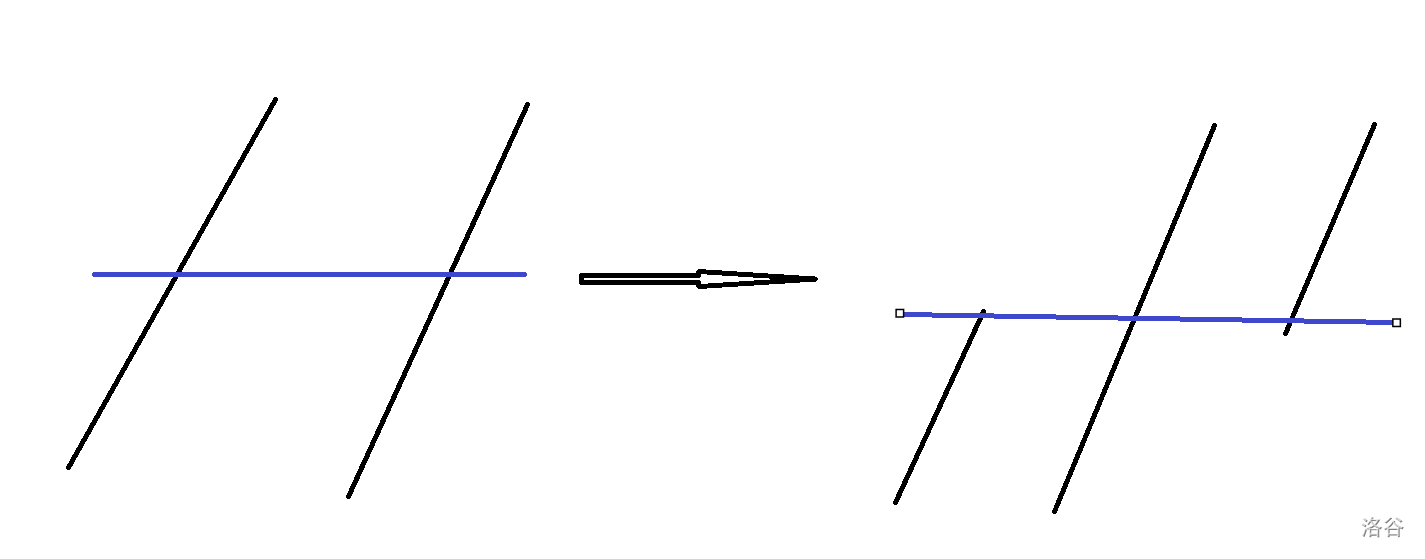
上半部分和下半部分是一个子问题。

于是就可以实现排序，分治地做下去即可。

分析一下复杂度，最外层的分治有 \(\log n\) 层，对值域分治聪明一点也是 \(\log n\) 层，合并两个不相交的序列，一层的代价总和是 \(O(n)\)，于是需要 \(O(n\log^2n)\) 次操作，能看出来常数是挺小的，可以过。

#include<iostream>
#include<algorithm>
#include<vector>
const int N = 5005; int n, a[N], b[N]; 
std::vector<std::pair<int, int>> rs, rs;
void ad(int l, int r){rs.push_back({l, r}); std::swap(a[l], a[r]);}
void mg(int l, int r){
    int f = 0, md = l, p1 = l, p2 = r;
    for(int i = l; i < r; i++) f |= (a[i] > a[i + 1]);
    if(f == 0) return; while(a[md] < a[md + 1]) md++;
    for(int i = l; i <= r; i++) b[i] = a[i];
    std::nth_element(b + l, b + md, b + r + 1);
    while(a[p1] <= b[md]) p1++; while(a[p2] > b[md]) p2--;
    for(int i = p1, j = md; i < j; i++, j--) ad(i, j);
    for(int i = md + 1, j = p2; i < j; i++, j--) ad(i, j);
    for(int i = p1, j = p2; i < j; i++, j--) ad(i, j);
    mg(l, md), mg(md + 1, r);
}
void divide(int l, int r){
    if(l == r) return; int md = l + r >> 1;
    divide(l, md), divide(md + 1, r), mg(l, r);
}
int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(0),std::cout.tie(0);
    std::cin >> n; 
    for(int i = 1; i <= n; i++) std::cin >> a[i];
    divide(1, n); rs = rs; rs.clear();
    for(int i = 1; i <= n; i++) std::cin >> a[i];
    divide(1, n); std::reverse(rs.begin(), rs.end());
    for(auto x:rs) rs.push_back(x);
    std::cout << rs.size() << '\n';
    for(auto [l, r] : rs) std::cout << l << ' ' << r << '\n';
}