一套模板搞定二叉树算法题--二叉树算法讲解001

1、二叉树定义

2、二叉树存储结构

2.1、经典题目代码构建

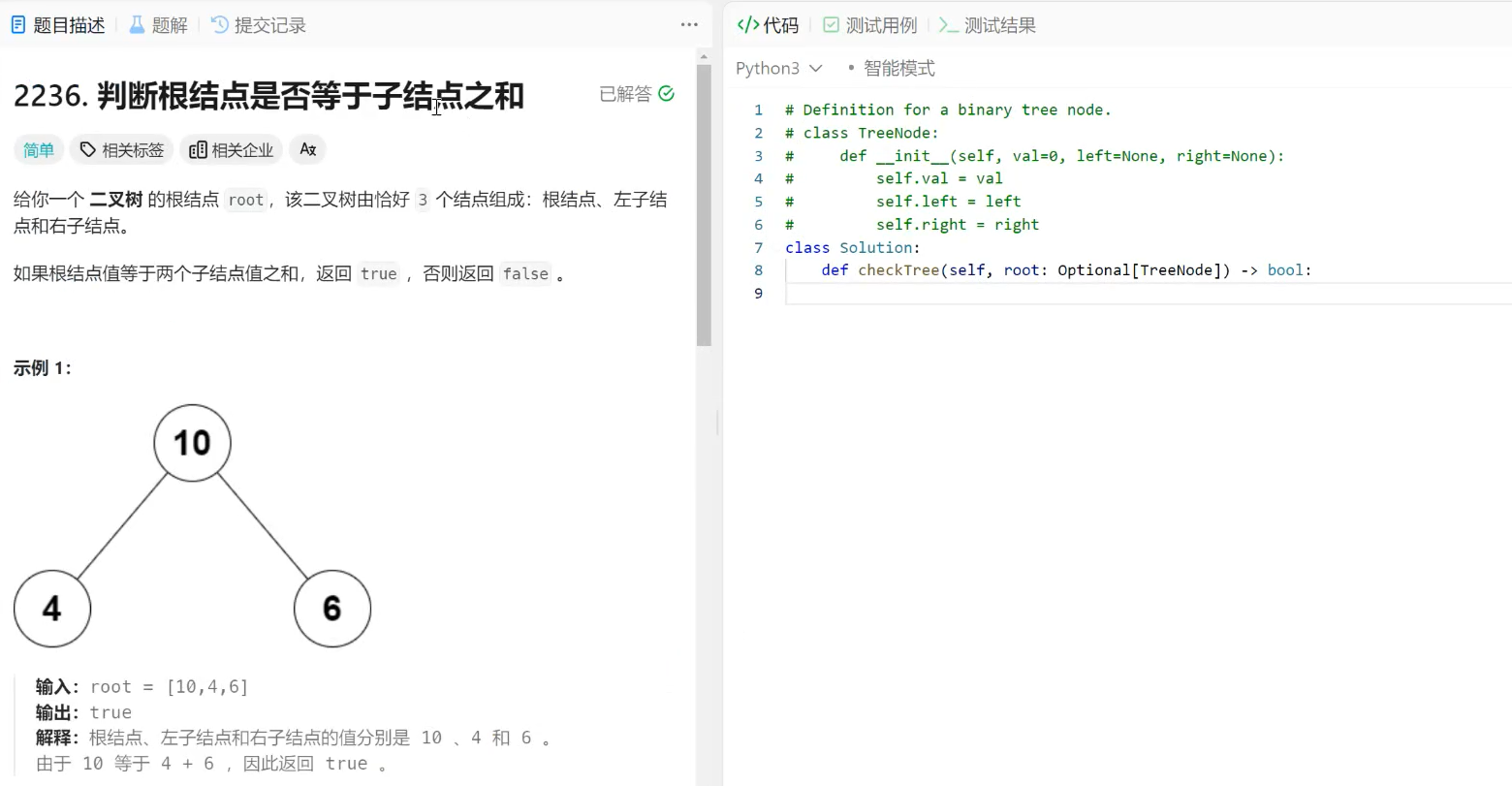
代码构建：

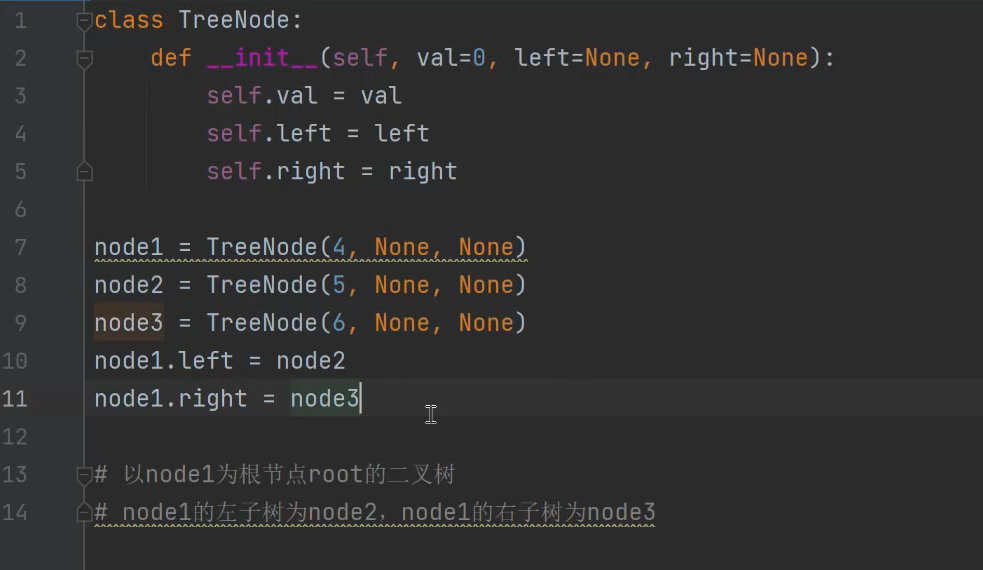
代码对应的二叉树的图：

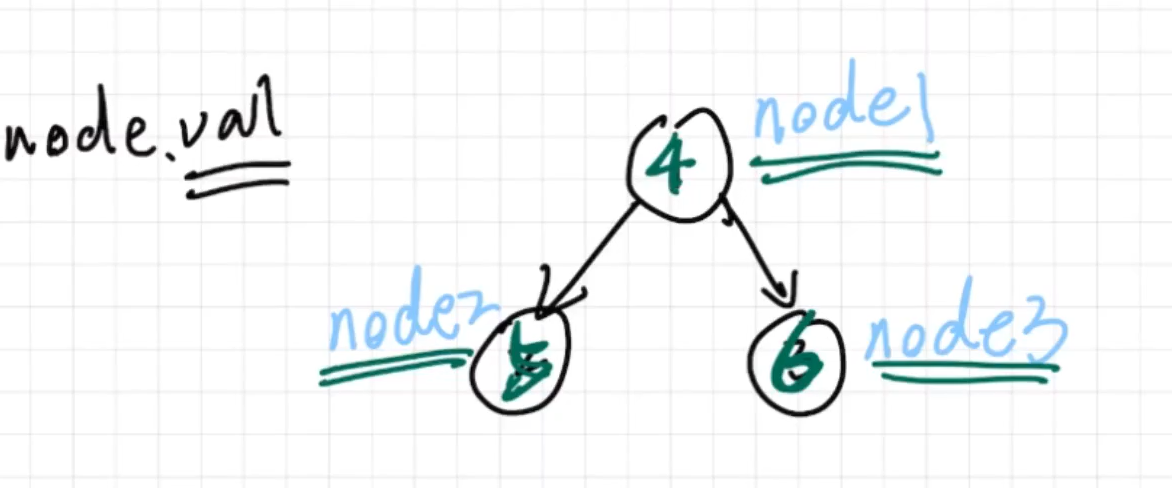
一行代码搞定lettcode2236，运行通过；就是考察对二叉树结构的理解：

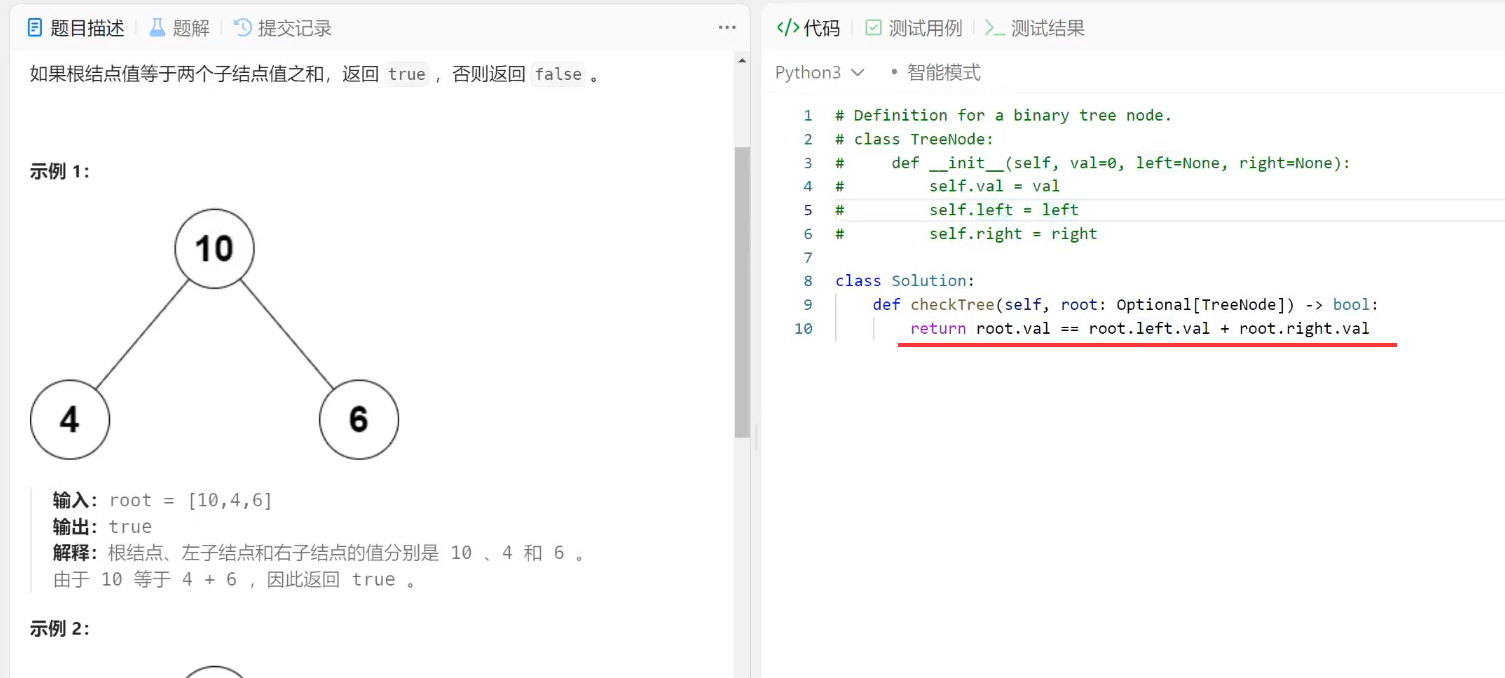
3、深度优先遍历DFS和广度优先遍历BFS概念

3.1、深入讲解广度优先遍历BFS

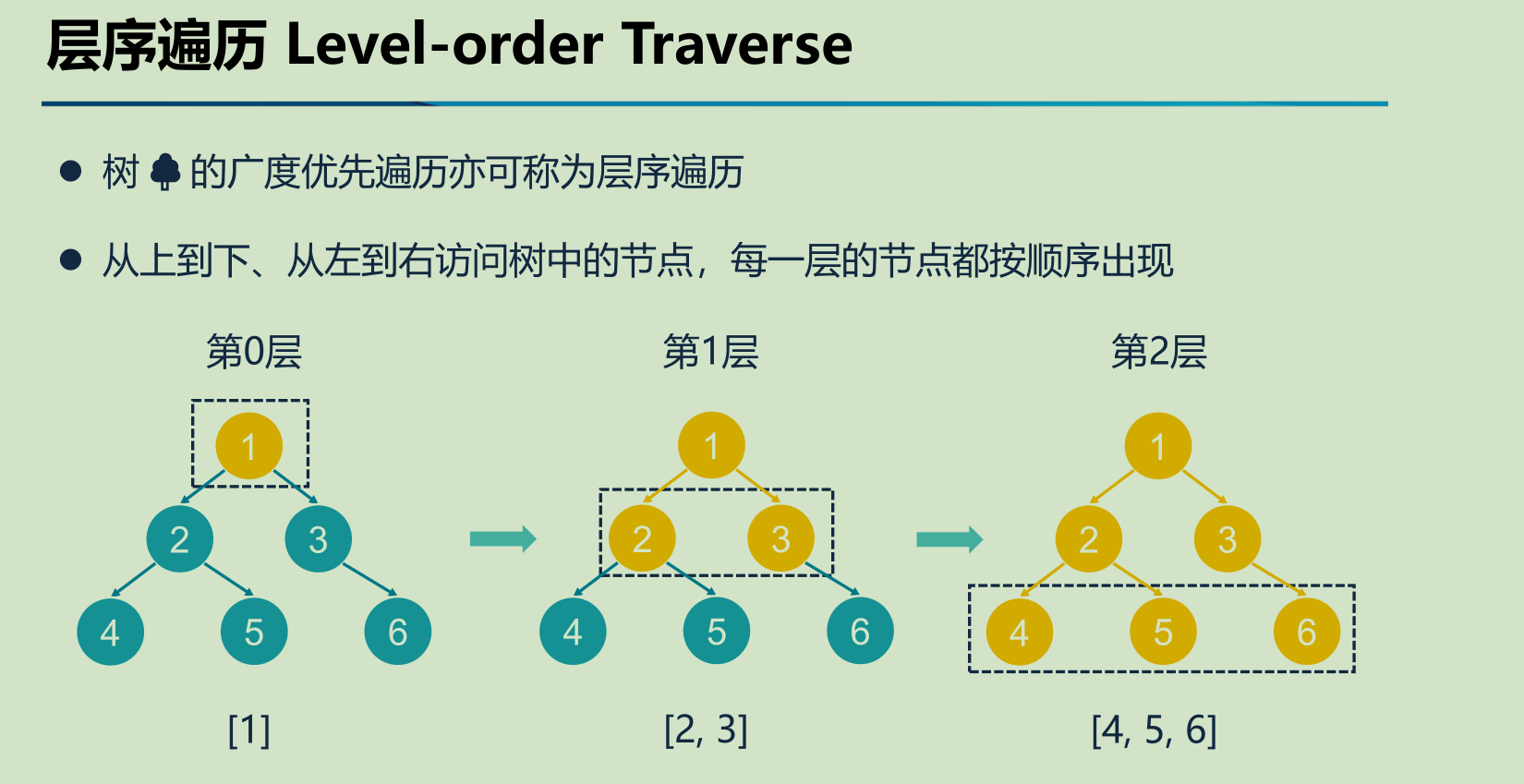
树的 广度优先遍历BFS 也可以称之为层序遍历

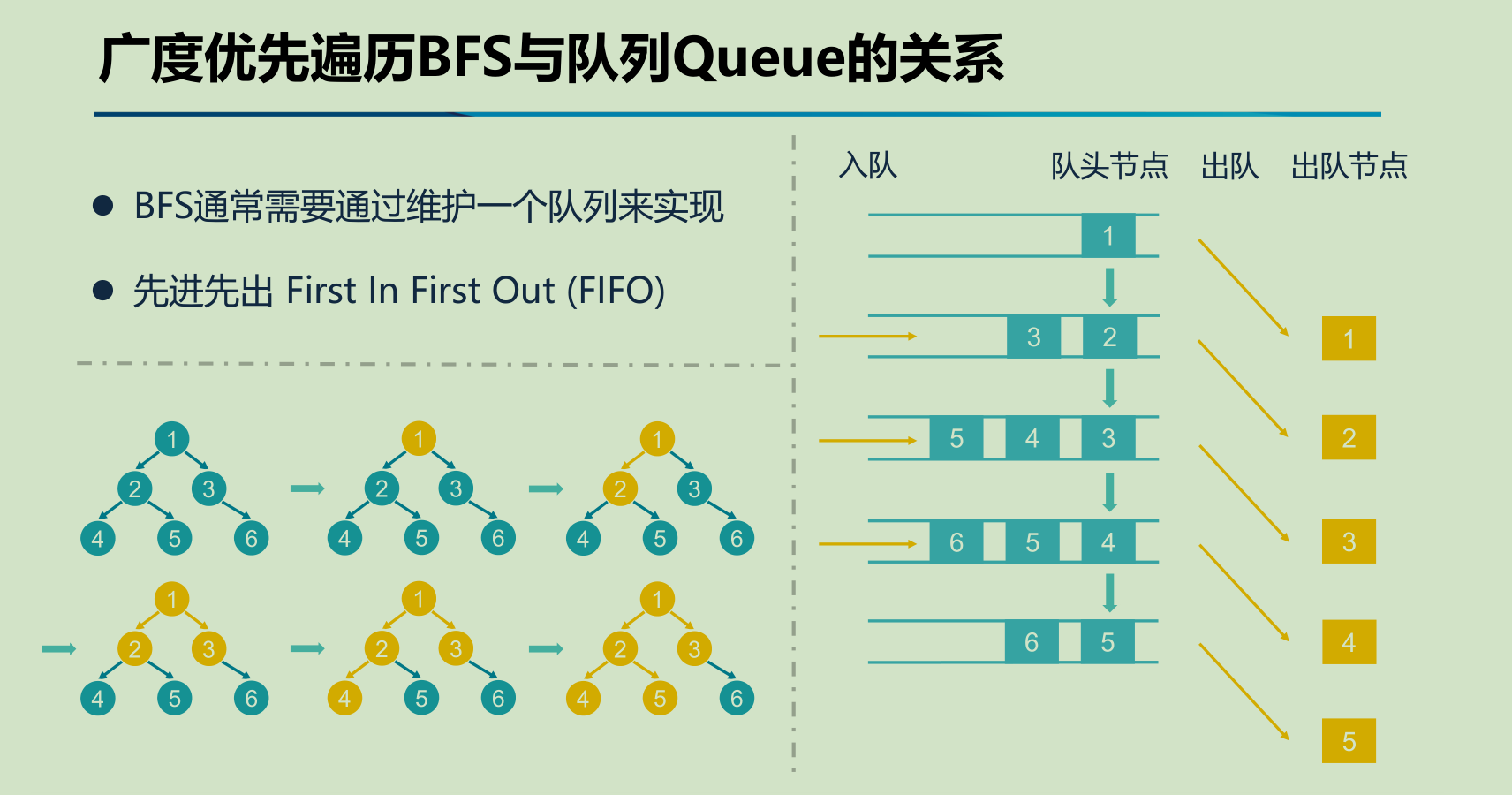
广度优先遍历BFS与队列Queue的关系图：

队列基础知识

结合队列基础知识中对于popleft()函数的讲解，会发现上面的 广度优先遍历BFS与队列Queue的关系图
在绘制时，左右方向上可能搞反了，不太容易理解。

所以重新绘制一个左右方向容易理解的版本的广度优先遍历BFS与队列Queue的关系图 :

4、万能模板经典题

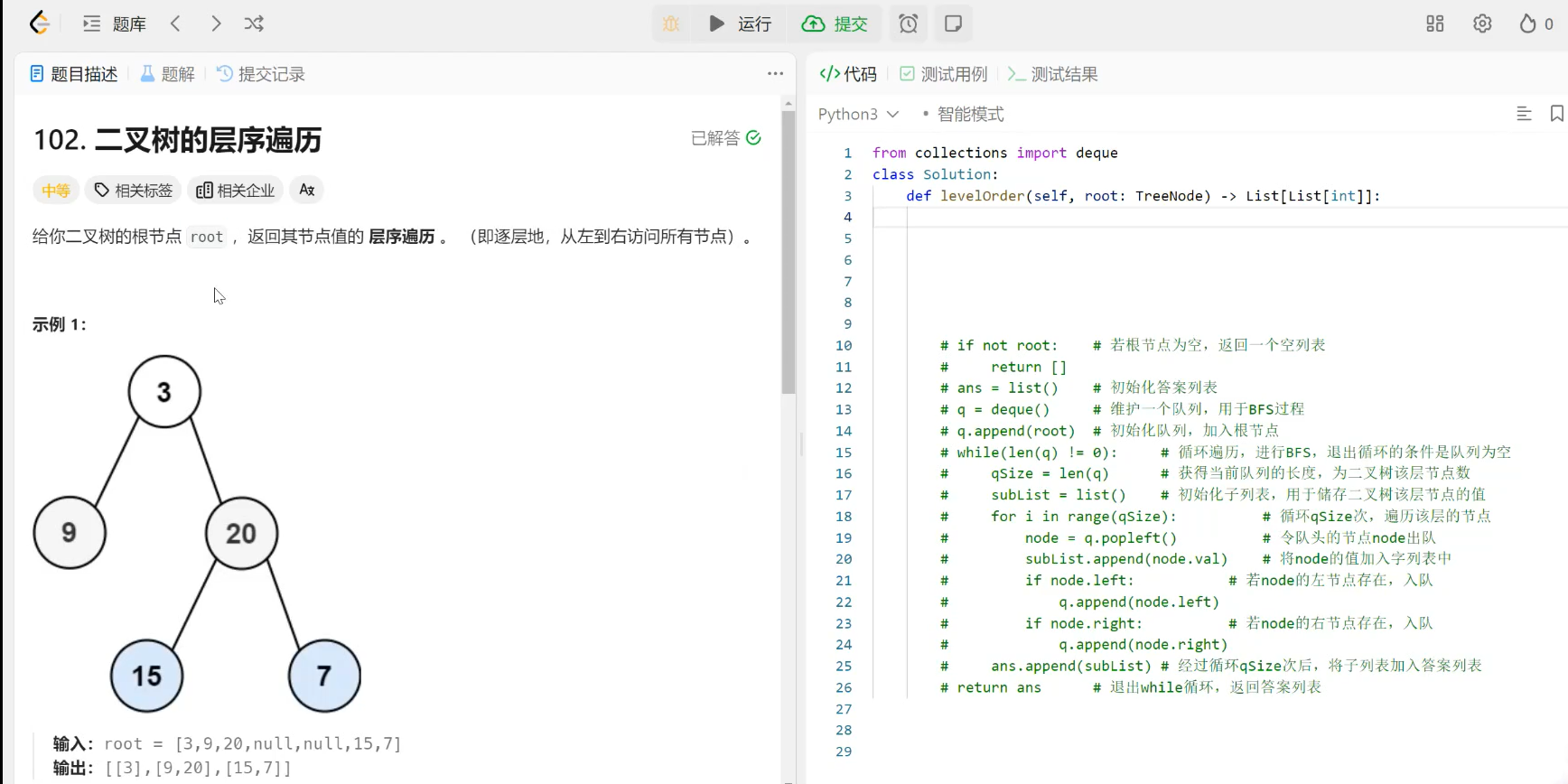
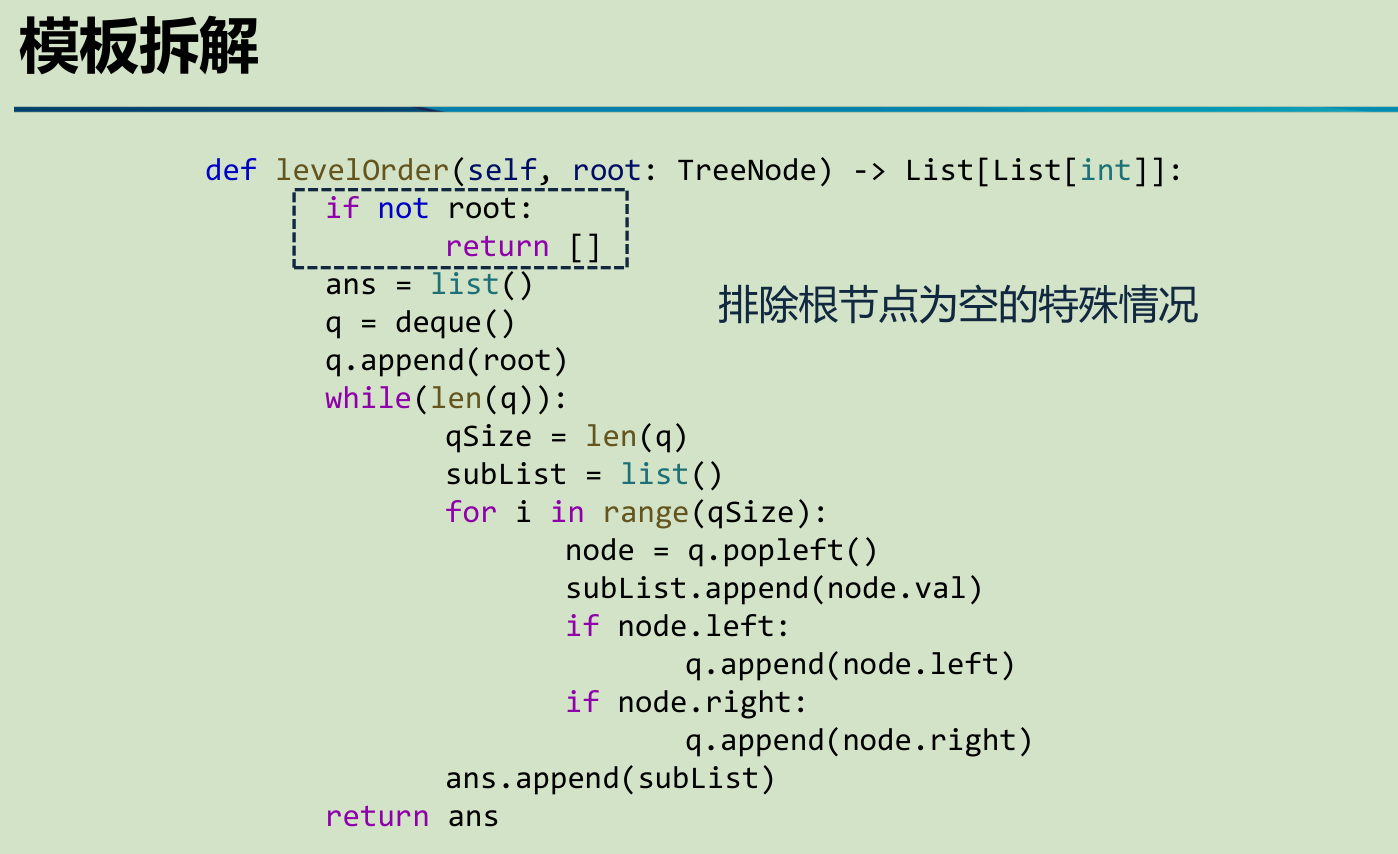
4.1、LeetCode102

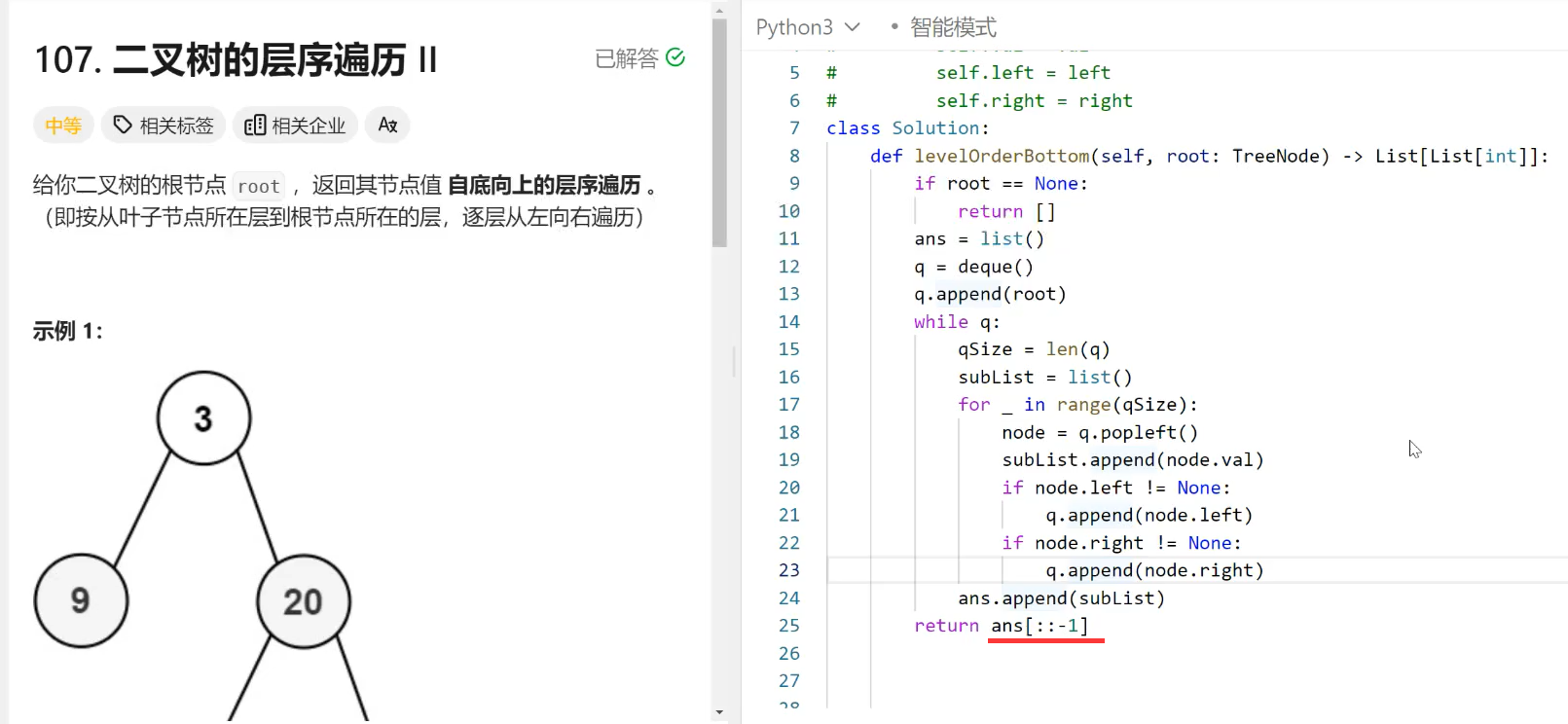
4.2、LeetCode107

和102题相同的模板，代码几乎相同，只需要在最后一行用切片的写法做一个反转即可：

4.3、LeetCode103

题目：

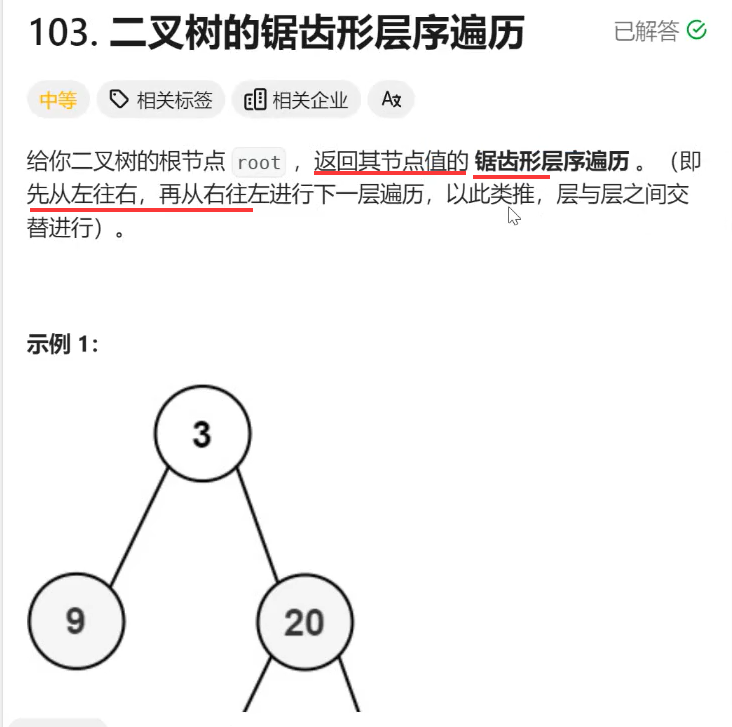
题意：

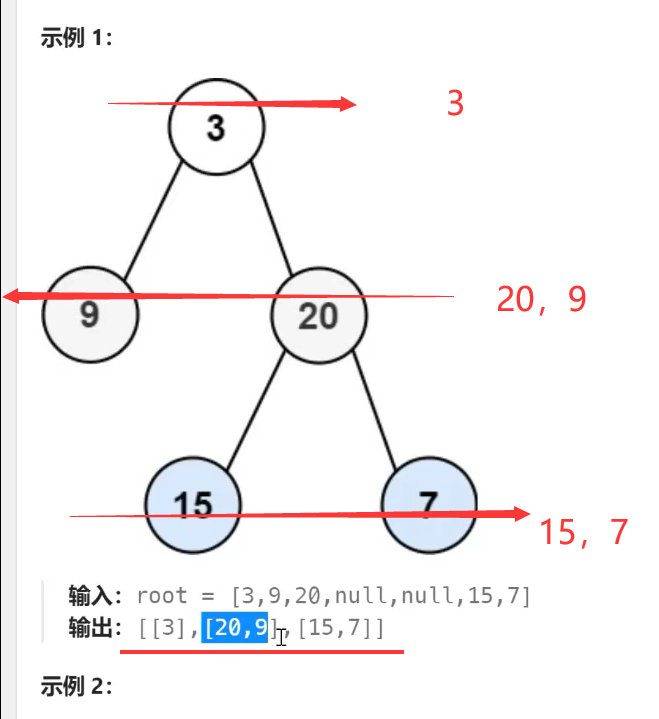
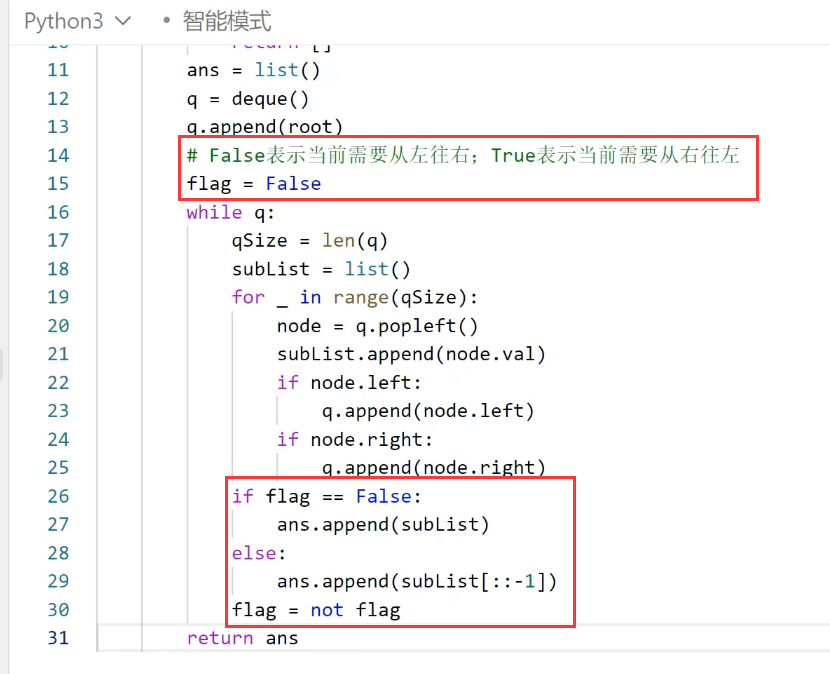
题解：
只需要在模板的基础上，添加一个Flag标志，标记从左往右或者从右往左即可。

4.4、LeetCode637

这连续几道题，都提到二叉树的 层 的概念，就可以很明显的考虑到是要用层序遍历 来做。
题目：

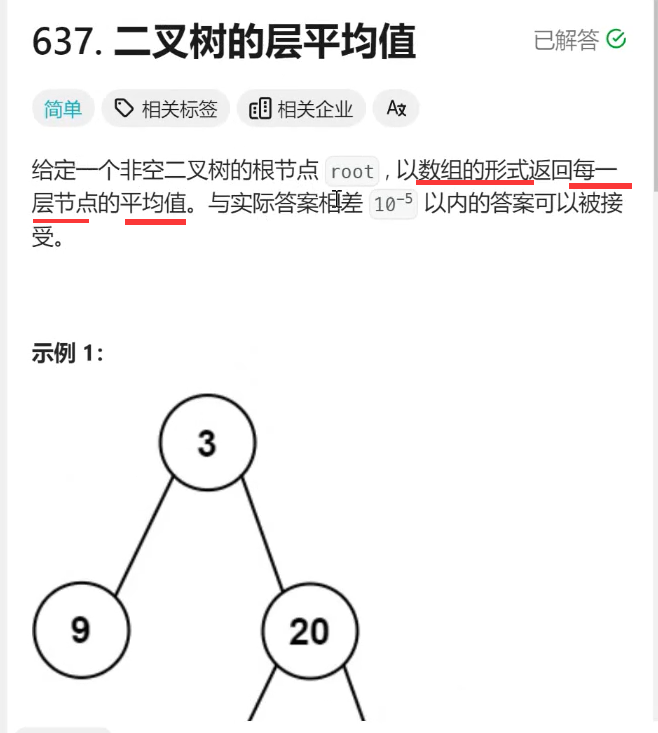
题意：

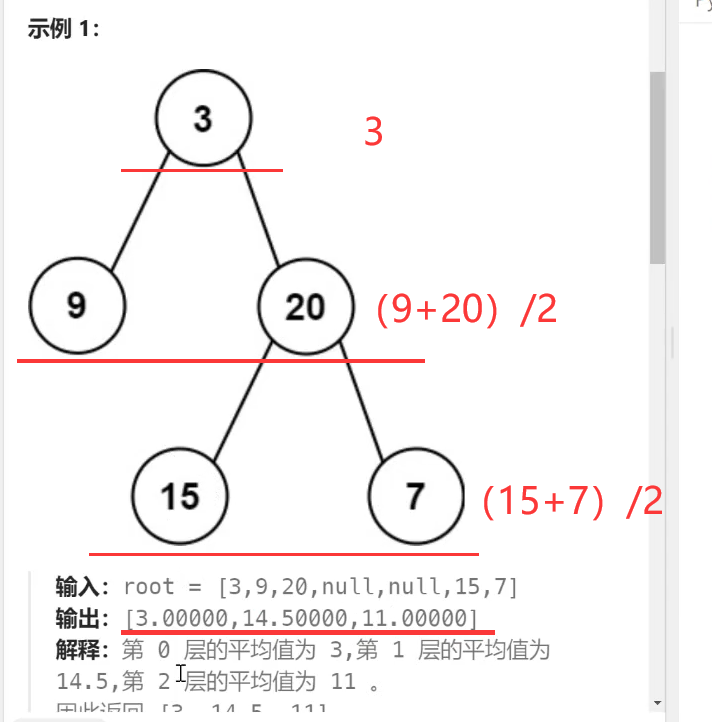
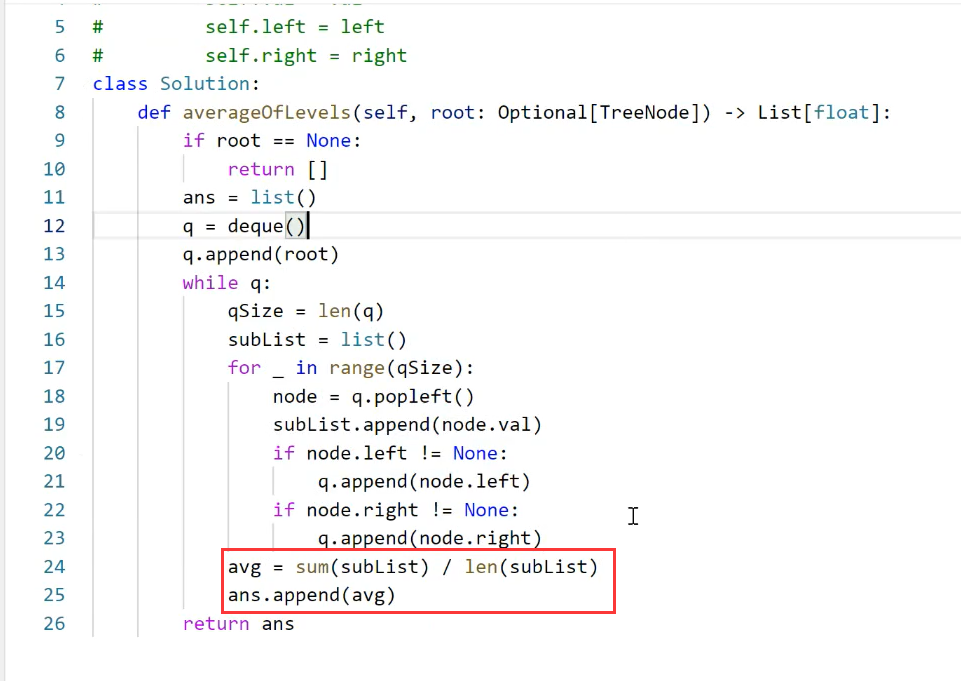
题解：
基于模板，最后添加元素处改一下，由添加层列表，即（每一层的所有节点），改为添加每一层所有节点的平均值即可。

4.5、LeetCode199

题目：

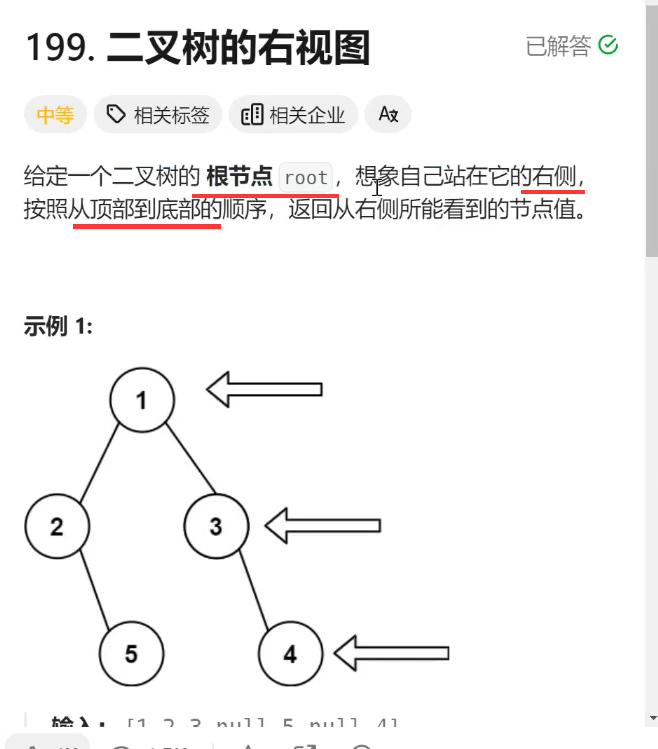
题意：

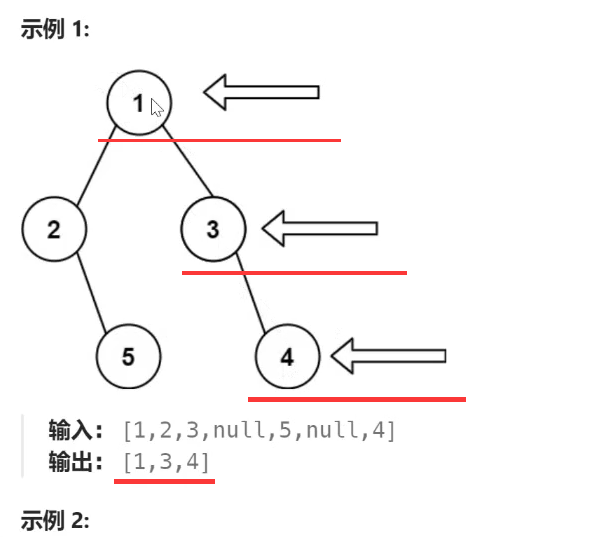
题解：
根据题意，实际上这道题问的是每一层 的最右边的元素是什么？
所以还是涉及到层 的概念，还是要用层序遍历 来做。然后再每一层取出最右边的元素即可。

基于模板，只改一下最后的添加，由添加层列表，改为添加每一层的最后一个元素即可。

如果不用模板，不用层列表sublist，也可以修改为如下代码：

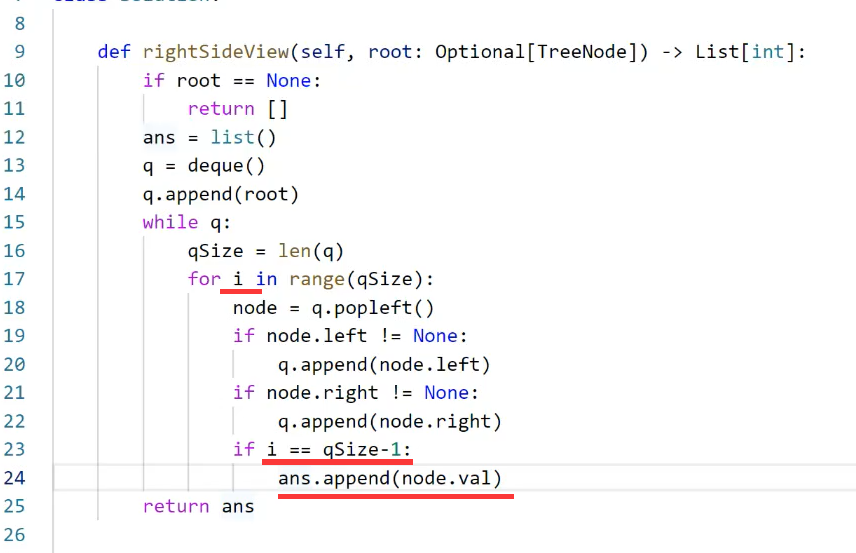
这样就不用额外的空间去存每一层的所有节点。只在每一层的最后一个节点去判断，然后添加最后一个节点到总的列表。

这道题，不是一个明显的层序遍历的题，但是仔细分析题意，思路转换，还是能结合层序遍历模板来解题的。

4.6、LeetCode513

题目和题意：

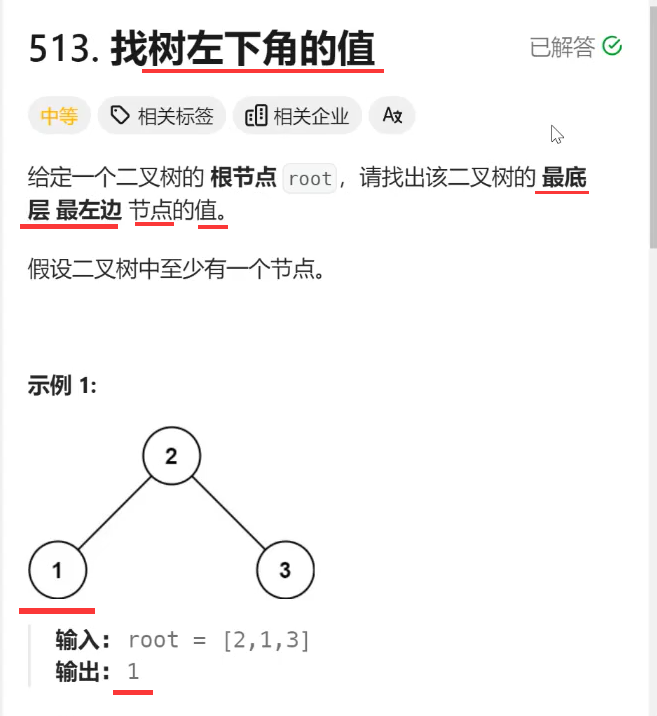
题解：
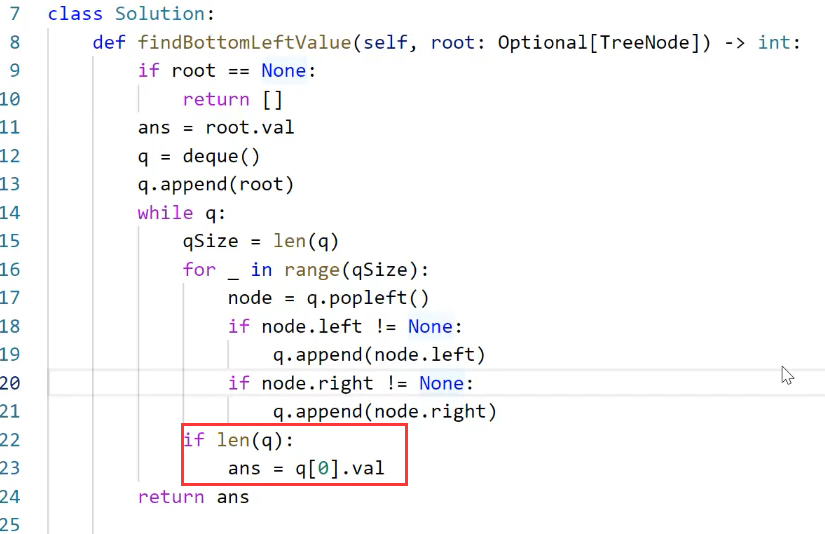
基于模板，只需要改动最终的返回ans，ans的初始化由初始化为list改为初始化为root.val，即初始化为根节点的值。
ans的返回由添加层列表，改为添加层的左侧第一个元素的值。

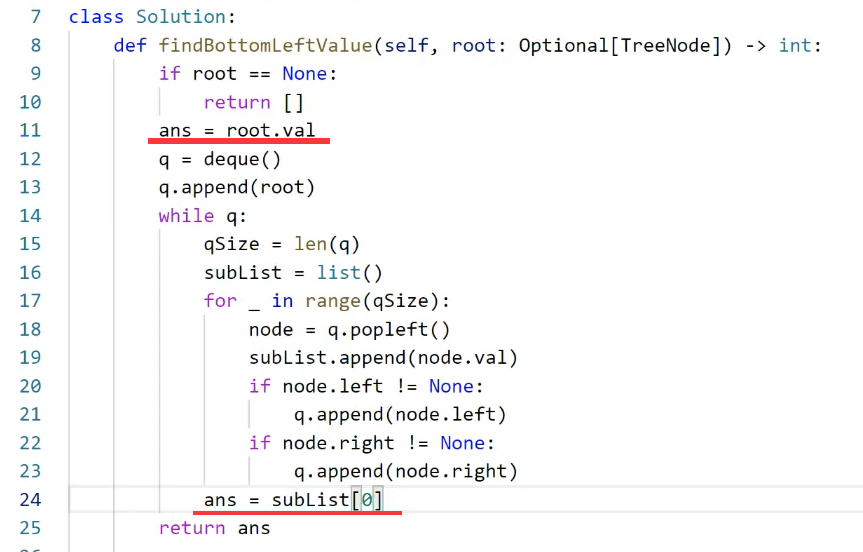
考虑内存空间的情况，可以进一步优化为如下代码：
1和2都可以解决问题
1、

2、

4.7、LeetCode515

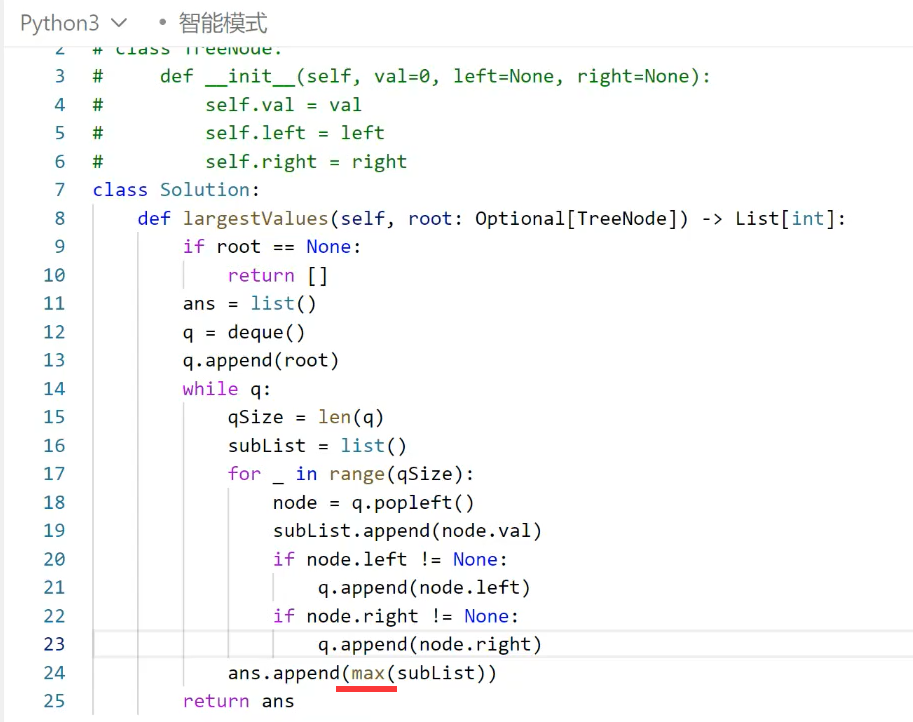
题目和题意：

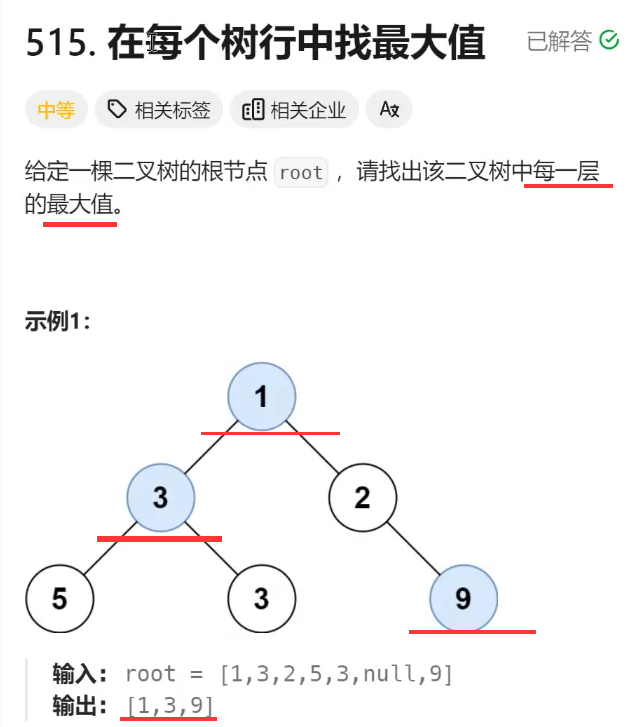
题解：
模板改最后一行添加层列表的最大值即可。

4.8、LeetCode1161

题目和题意：
这个题目还是需要仔细读一下的：

题解：
1、先解决层号的问题，输出层号

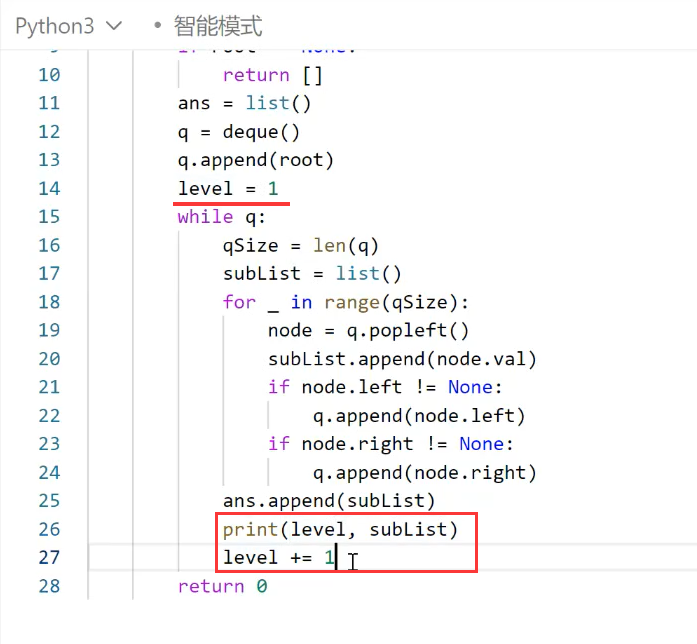
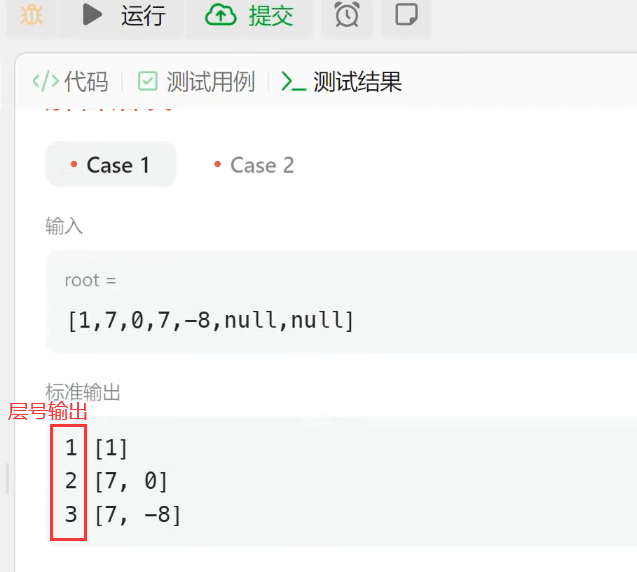
2、题解完成：

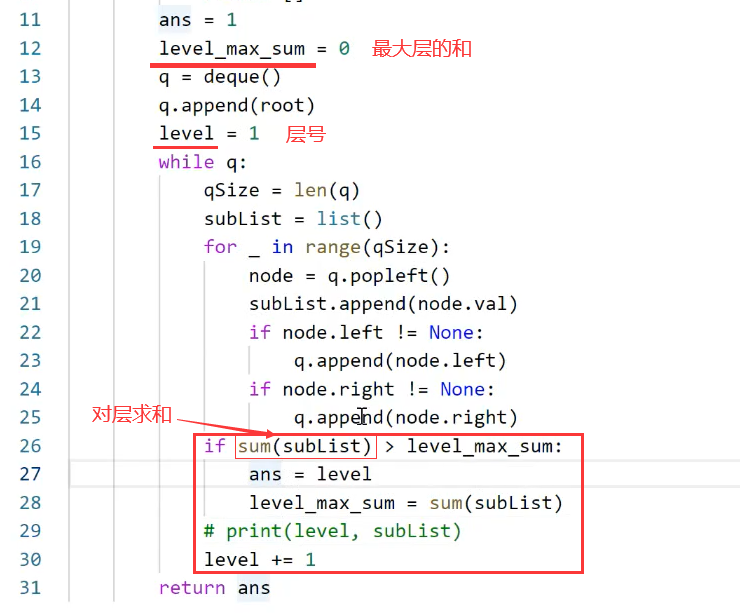
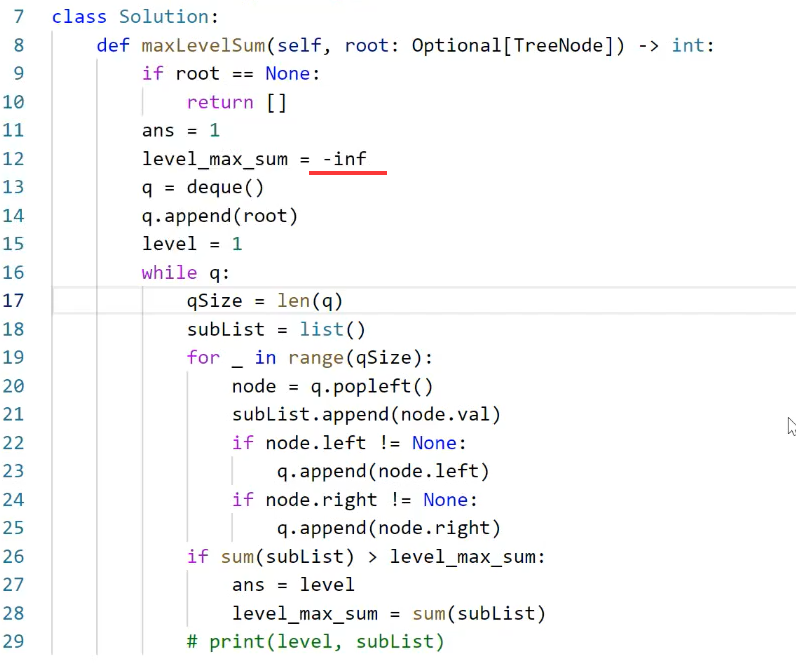
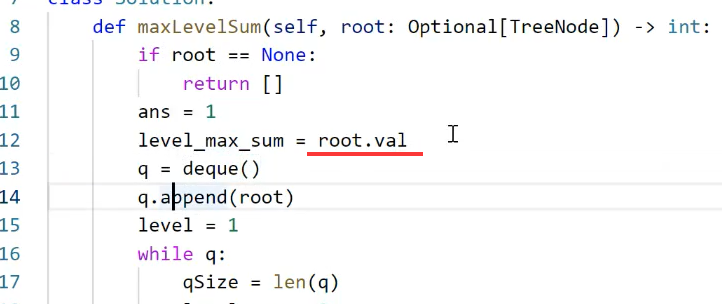
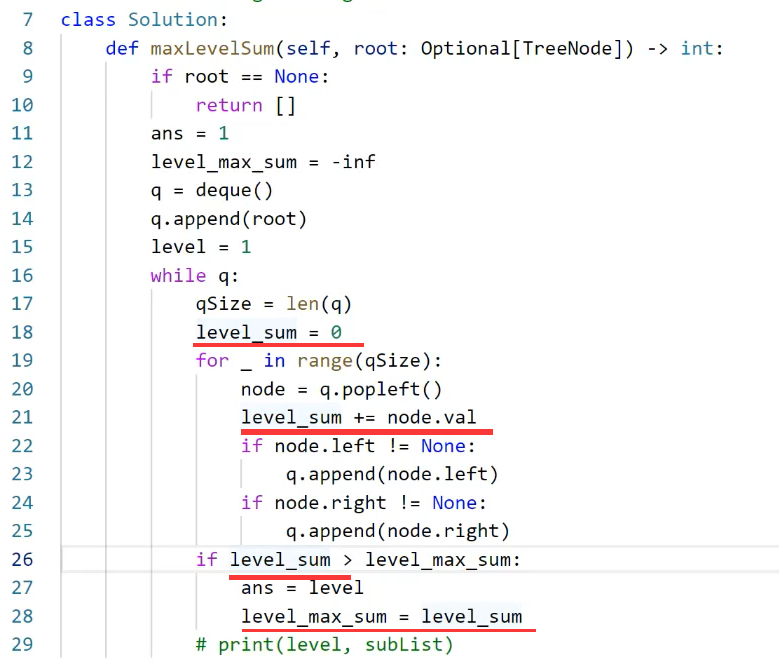
考虑到节点值可能为负数的情况，最大层的和level_max_sum的初始化，由初始化为0改为初始化为负无穷-inf或者初始化为第一层的值root.val

对题解优化，尽量不要用标准sum函数api，因为它每次也要全部遍历，比较耗时。
不用sum函数的修改版：

4.9、LeetCode101

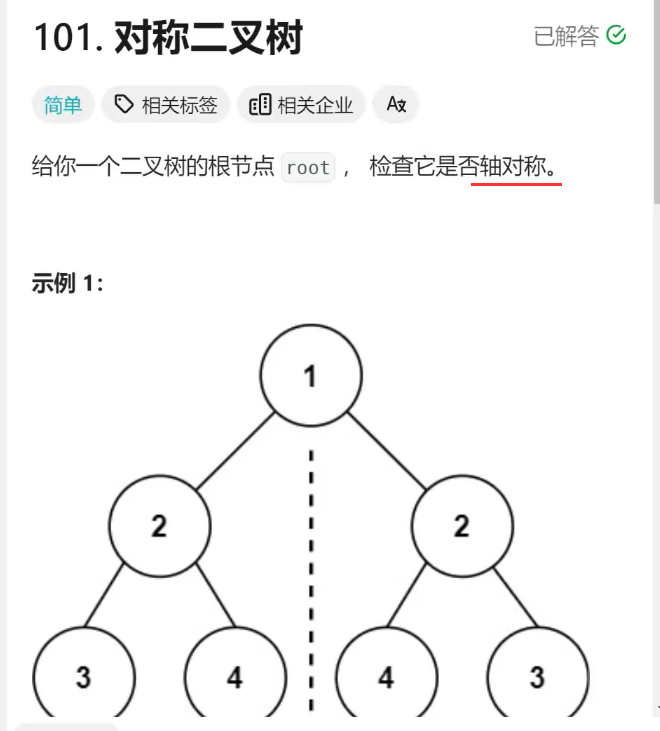
题目和题意：
示例1

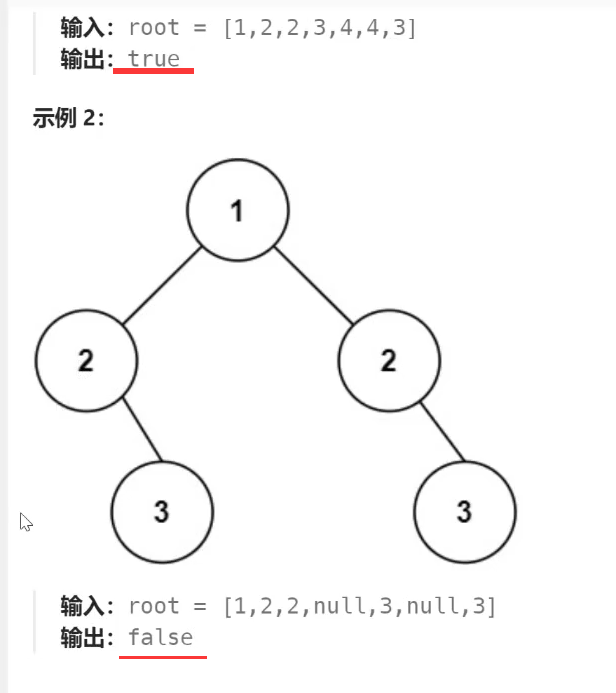
示例2

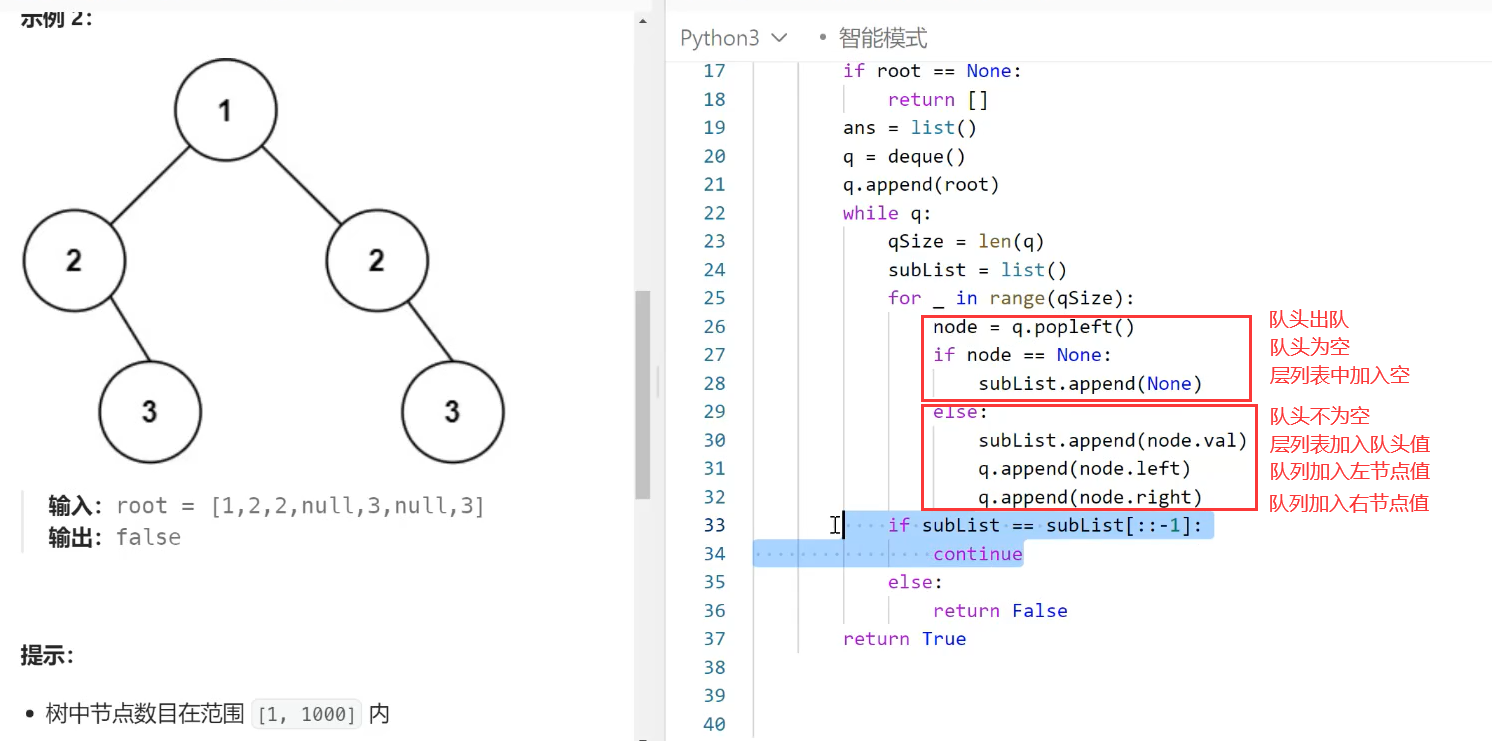
题解:
1、

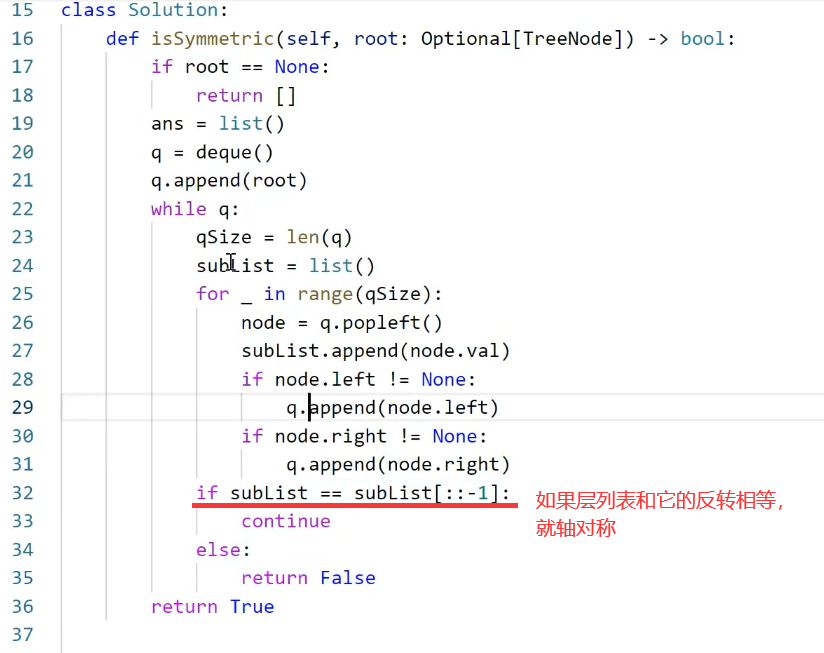
2、题解1中还是有问题，满足示例1图的情况，但是不满足示例2；
修改为如下代码后，同时满足示例1和示例2

4.10、LeetCode1302

题目：

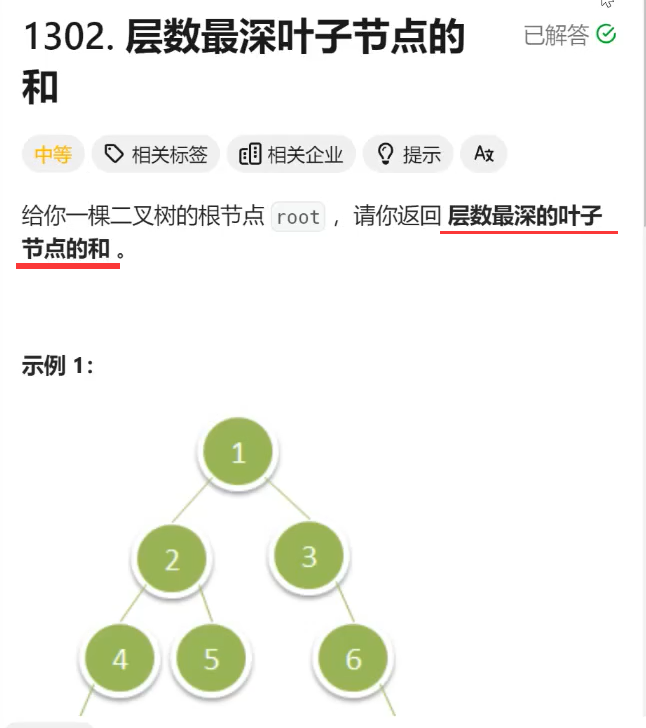
题意：
最深的那层这里就是第四层的7和8、最深的那层的节点就一定是叶子节点。

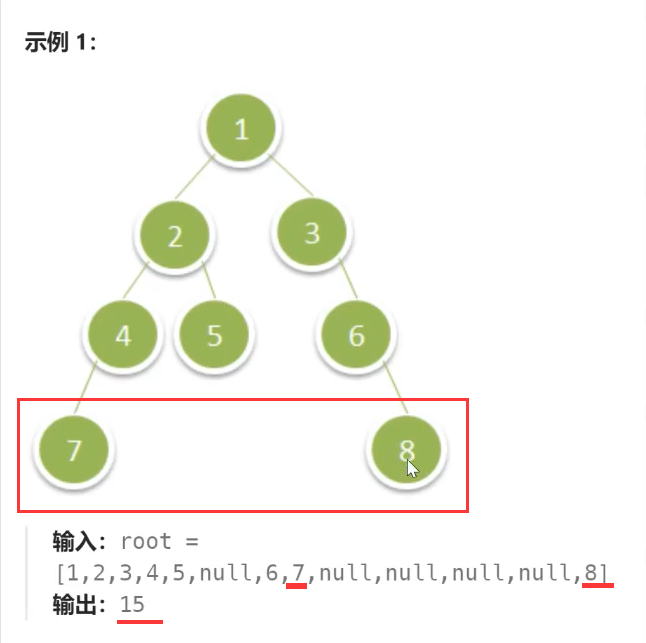
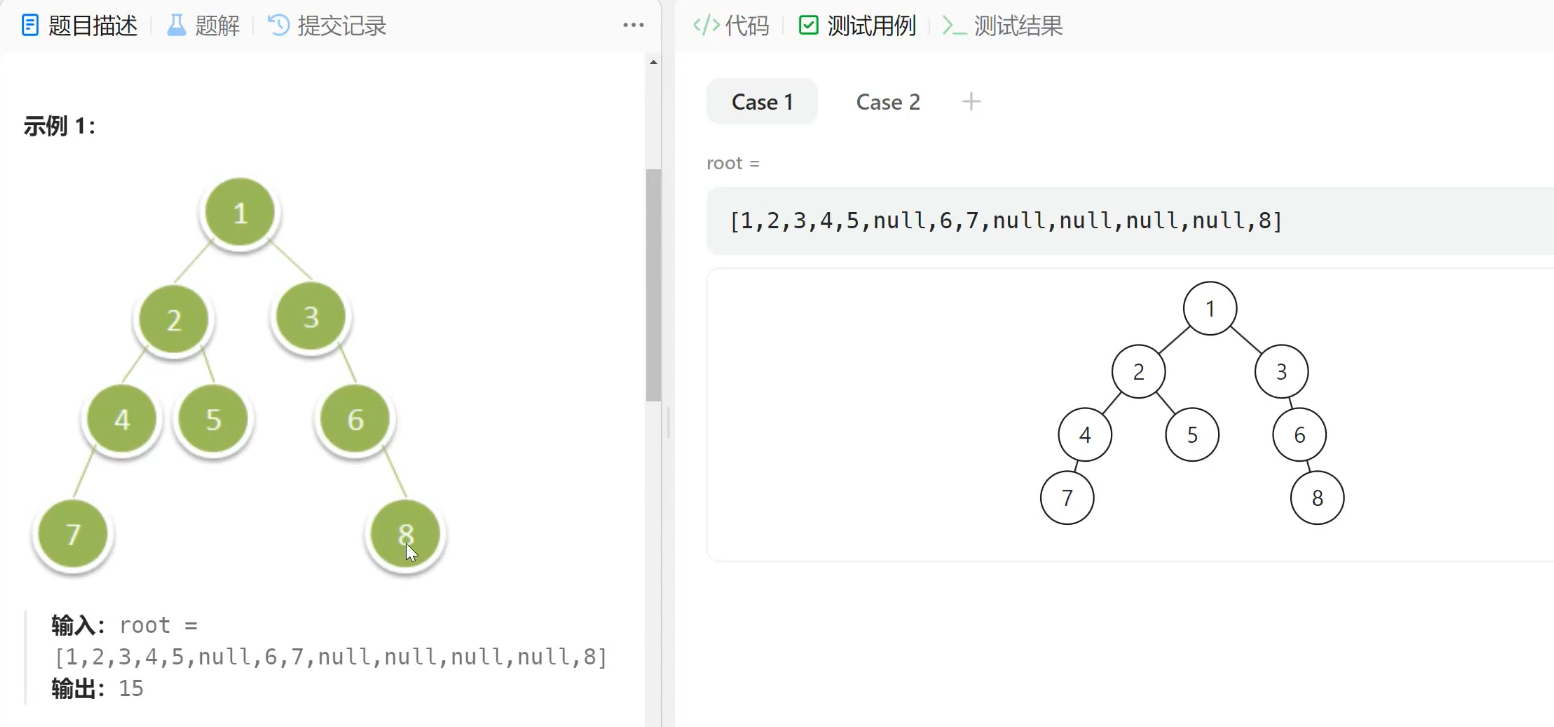
题解：
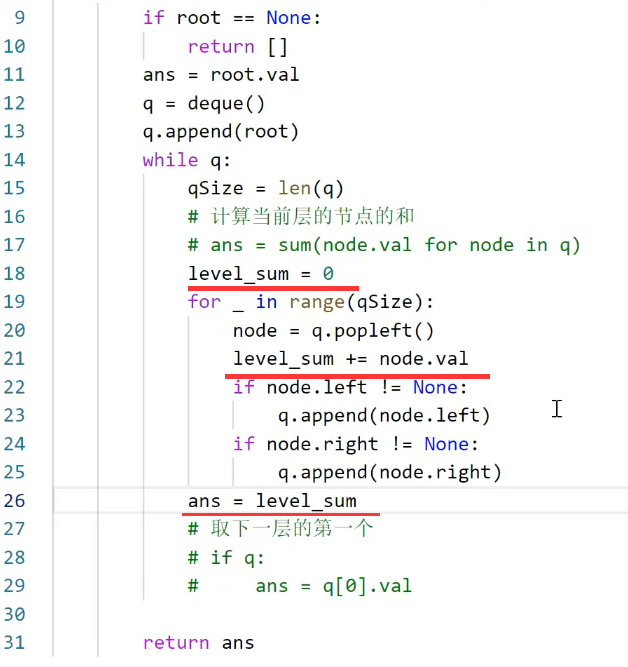
修改 4.6、LeetCode513 中的代码，将找左下角节点的值，改为求和即可。

不用sum函数的优化版：

5、总结

最核心知识点：
BFS与队列的关系

leetcode102题引申出的万能模板：

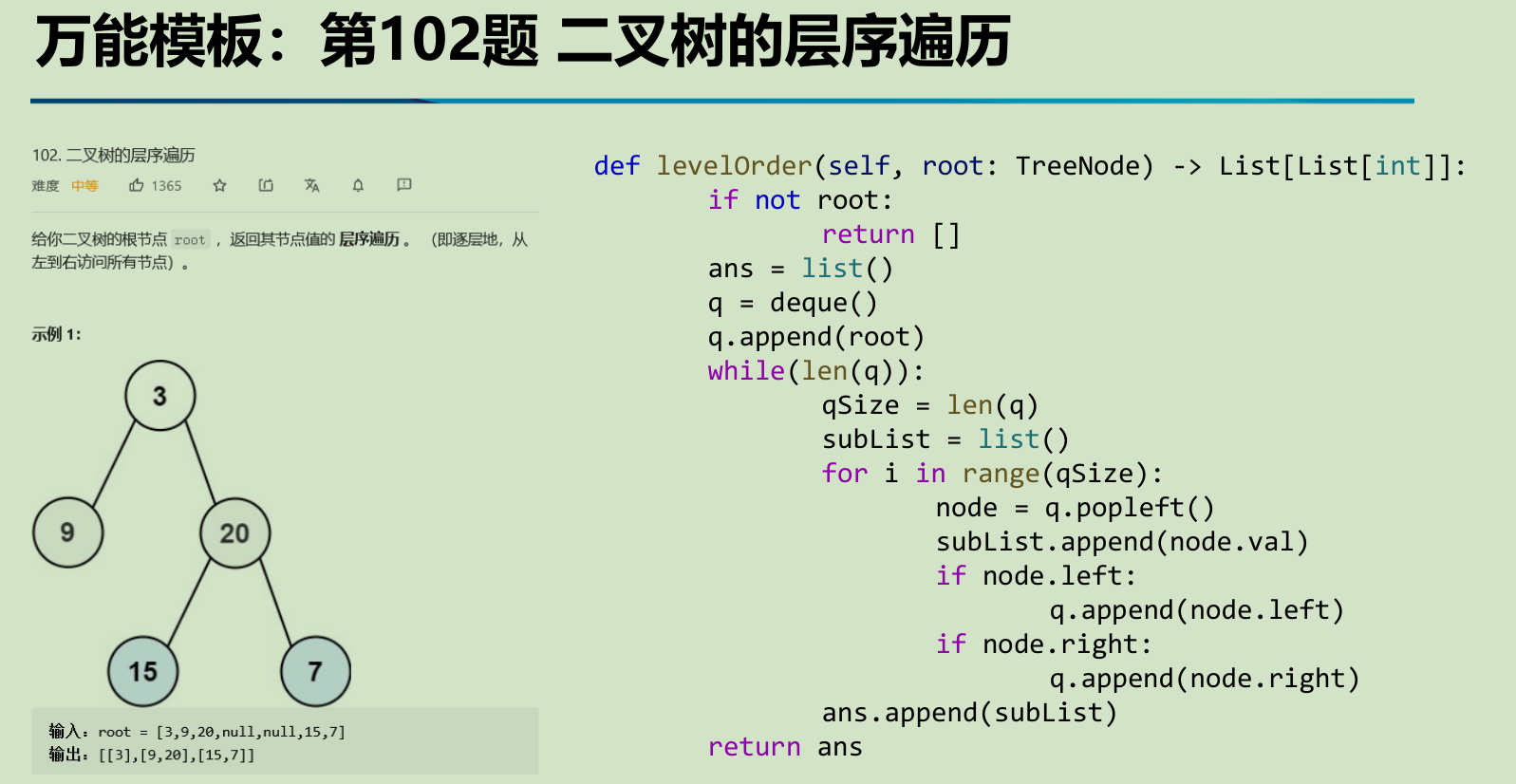
模板代码及测试

from collections import deque
from typing import List

class TreeNode:
def init(self,val=0,left=None,right=None):
self.val = val
self.left = left
self.right = right

def levelOrder(root) -> List[List[int]]:
# if root is None:
# if root == None:
if not root:
return []
ans = list()
q = deque()
q.append(root)
# while len(q) > 0:
# while len(q):
while q:
qSize = len(q)
subList = list()
# for i in range(qSize):
for _ in range(qSize):
node = q.popleft()
subList.append(node.val)
# if node.left != None:
if node.left:
q.append(node.left)
# if node.right != None:
if node.right:
q.append(node.right)
ans.append(subList)
return ans

if name == 'main':
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.left = TreeNode(6)
root.right.right = TreeNode(7)
root.left.left.left = TreeNode(8)
result = levelOrder(root)

打印结果

print(result)

6、练习题

---

注：
文中截图源自大佬： 闭着眼睛学数理化 课程内容