数据结构和算法:树型数组

1. 前言

什么是树型数组? 顾名思义,树型数组就是用数组来模拟树形结构.
有什么用? 可以解决大部分基于区间上的更新以及求和问题 : 比如求一个数组的1~m之间的和,多次操作,它的复杂度在O(mn),这个问题使用树型数组就更高效.

2. 树型数组介绍

介绍树型数组之前,需要先介绍树型数组中最重要的一个lowbit概念.

2.1 lowbit

程序员经常会碰到一个面试题: 如何得到一个数它的二进制位中1的个数. 一个很优的解法是利用销位(x&(x-1))能够将最右边的1置0.
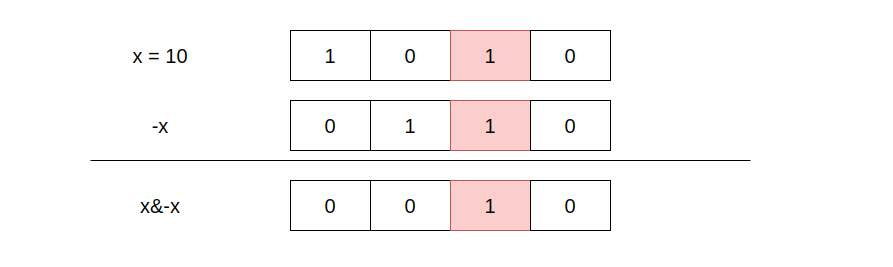
lowbit和这个解法相似,它的定义是:二进制表达式中最右边的1所对应的值. 比如, 10的二进制是0x1010, 那么lowbit(10) = 0x10 = 2. 计算公式是:

lowbit(x) = x & -x

计算机中整数采用补码表示,-x实际上是x按位取反再加1, 原本最右边的1变成0, 它右边的0变成1, 再加1后,因为进位,所以-x最右边的1的位置不会变,它右边的0也都不变,变的只有它左边都取反了 ; x和-x按位相与后, 最后只有x最右边的1保持为1,其他全为0.

lowbit在树型数组中非常重要.

2.2 树型数组的构建

先给出树型数组的构建规则, 对于一个长度为n的数组,A数组是原始数组,C数组是我们将要将A改造成树型数组的数组:

每个C[i]都管辖一定数量的元素,下表为i的数所管辖的元素个数为2^k个(k为i的二进制的末尾0的个数),如i=8(0x1000)时,末尾有3个0, C[8]管辖的个数是2^3=8个;
假设C[i]管辖的元素为m个,那么C[i] = A[i-m+1] + A[i-m] + .... + A[i]

很容易知道,所有奇数位的元素都只负责自己,因为它们的二进制位末尾没有0.

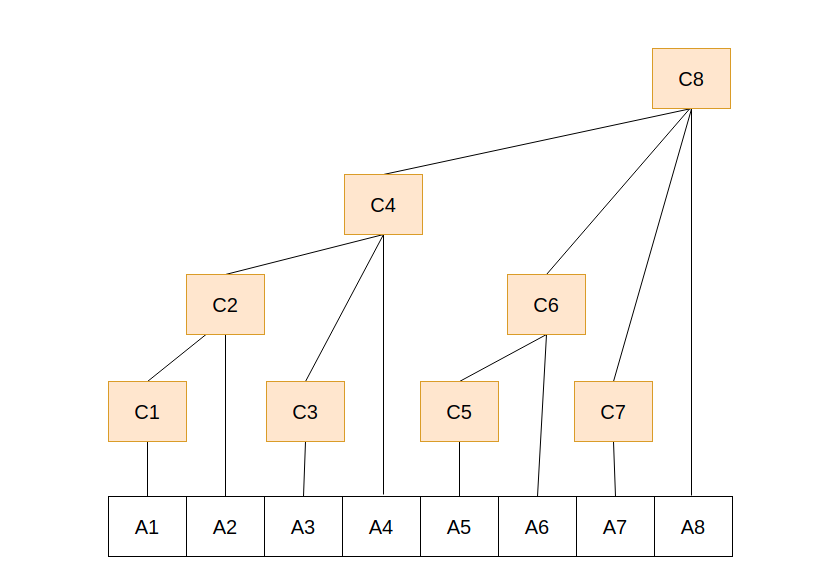
那么根据规则, 对于一个长度为8的数组,A数组是原始数组,C数组是我们将要将A改造成树型数组的数组. 这样构建C:

C1 = A1
C2 = C1 + A2 = A1 + A2
C3 = A3
C4 = C2 + C3 + A4 = A1 + A1 + A3 + A4
C5 = A5
C6 = C5 + A6 = A5 + A6
C7 = A7
C8 = C4 + C6 + C7 + A8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
....

建立起这个树型数组有什么用? 假设我们要求A1~Am的和Sum(m),且树型数组C已建立, 该怎么做呢?

观察一下:

sum(8) = C[8]  // 8 = 0x1000
sum(7) = C[7] + C[6] + C[4]  // 7 = 0x111
sum(6) = C[6] + C[4]  // 6 = 0x110
sum(5) = C[5] + C[4]  // 5 = 0x101
....

不知道大家发现没有,sum(m)和m的二进制形式关系很大,也就是它里面1的个数.

问题的关键是我们得知道对于m,用C中哪几个元素可以表示A1~Am的和呢?这里就要用到lowbit了:

    m = m - lowbit(m); //不断对m的二进制末尾的1进行消除,直到m==0 . 中间得到的m即为我们需要用到的C[m]

也即求数组A的前缀和Sum(m):

int sum(int m){
    int ans = 0;
    while(m > 0){
        ans += C[m];
        m -= lowbit(m);
    }
    return ans;
}

比如sum(8) = C[8](8清1位直接变0), sum(7)=C[7] + C[6] + C[4] (111 清0需要清两次: 110, 100).
还有一个问题就是进行数值更新,更新也是一样的,我们更新A[i]的话,对应就是更新C[i],但是C[i]的父节点也是一样要更新的,求它的父节点就和上面的过程反过来:

    m = m + lowbit(m);//不断使最后一位的1进位,直到m大于n即个数,中间产生的m都是我们需要修改的C[m]

更新代码如下:

void add(int x, int value){
    //注意这里是add,如果是update的话,value要转化成差值
    A[x] += value;    //继续维护原数组
    while(x <= n){
        C[x] += value;
        x += lowbit(x);
    }
}

实际上在第一次建立树型数组时,就可以按照更新的逻辑,当然前提是整个C数组要清零.

3. 总结

求和操作,使用lowbit(m)不断查找所关联的C数组元素;
更新操作,使用lowbit(m)不断查找自己的C数组父节点元素;
查询操作,如果保存原数组并维护,那么直接查原数组更方便,如果不保存,就比较麻烦,通过sum(m)-sum(m-1)得到是一种思路.
树型数组执行前缀和操作的单次效率是O(logn), 多次效率是O(mlogn);更新效率也一样;查询效率借助原数组的话可以是O(1),如果为了节省空间不是有原数组,那么就比较麻烦,需要使用sum(m)-sum(m-1)得到.

注意: 数组下标要从1开始.

主要就是add和sum操作,建立树的过程我们都不用关心,非常方便.

4. 代码

最后给出一个完整代码:

#ifndef SRC_BASE_ARRAY_TREE_ARRAY_H_
#define SRC_BASE_ARRAY_TREE_ARRAY_H_

#include <vector>

namespace base {

// Note: Index of array is from 1 to size()
template <typename T>
class TreeArray {
 public:
  TreeArray(const int size)
      : origin_data_(size + 1, 0), tree_data_(size + 1, 0), size_(size) {}

  ~TreeArray() = default;

  // Note: Start from 1
  T sum(int index) {
    int res = 0;

    while (index > 0) {
      res += tree_data_[index];
      index -= lowbit(index);
    }

    return res;
  }

  void add(int index, T data) {
    origin_data_[index] += data;

    while (index <= size_) {
      tree_data_[index] += data;
      index += lowbit(index);
    }
  }

  void set(int index, T data) { add(index, data - origin_data_[index]); }

  T get(int index) { return origin_data_[index]; }

  int size() { return size_; }

 private:
  int lowbit(const int num) { return num & (-num); }

  std::vector<T> origin_data_;
  std::vector<T> tree_data_;
  int size_;
};

}  // namespace base

#endif  // SRC_BASE_ARRAY_TREE_ARRAY_H_

测试代码:

base::TreeArray<int> tree(100);
for(int i = 1; i <= 100; i++) {
    tree.set(i, i);
}

LOG(WARNING) << "-----0-------" << tree.get(50);
LOG(WARNING) << "-----1-------" << tree.get(100);
LOG(WARNING) << "-----2-------" << tree.sum(50);
LOG(WARNING) << "-----3-------" << tree.sum(100);
tree.add(50, 1);
LOG(WARNING) << "-----0-------" << tree.get(50);
LOG(WARNING) << "-----4-------" << tree.sum(50);
LOG(WARNING) << "-----5-------" << tree.sum(100);
tree.set(50, 50);
LOG(WARNING) << "-----0-------" << tree.get(50);
LOG(WARNING) << "-----6-------" << tree.sum(50);
LOG(WARNING) << "-----7-------" << tree.sum(100);

运行结果:

[1150:1150:0527/170551.372410:WARNING:thread_test.cc(201)] -----0-------50
[1150:1150:0527/170551.372463:WARNING:thread_test.cc(202)] -----1-------100
[1150:1150:0527/170551.372481:WARNING:thread_test.cc(203)] -----2-------1275
[1150:1150:0527/170551.372501:WARNING:thread_test.cc(204)] -----3-------5050
[1150:1150:0527/170551.372519:WARNING:thread_test.cc(206)] -----0-------51
[1150:1150:0527/170551.372537:WARNING:thread_test.cc(207)] -----4-------1276
[1150:1150:0527/170551.372556:WARNING:thread_test.cc(208)] -----5-------5051
[1150:1150:0527/170551.372573:WARNING:thread_test.cc(210)] -----0-------50
[1150:1150:0527/170551.372591:WARNING:thread_test.cc(211)] -----6-------1275
[1150:1150:0527/170551.372608:WARNING:thread_test.cc(212)] -----7-------5050

posted @ 2020-05-27 17:30 星星,风,阳光阅读(377) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

星星,风,阳光