算法导论(第三版)练习 2.3-1 ~ 2.3-7
2.3-1
【31,41】,52,26,38,57,9,49
31,41,【26,52】,38,57,9,49
【26,31,41,52】,38,57,9,49
26,31,41,52,【38,57】,9,49
26,31,41,52,38,57,【9,49】
26,31,41,52,【9,38,49,57】
【9,26,31,38,41,49,52,57】
2.3-2
js代码:
static merge2(arr, start, mid, end) { let left = arr.slice(start, mid); // arr[mid] is excluded let right = arr.slice(mid, end); let i = 0, j = 0; // index of left and right let k = start; // index of arr while(i < left.length && j < right.length) { arr[k++] = left[i] < right[j] ? left[i++] : right[j++]; } if (i == left.length) { left = right; i = j; } else { i = i; } while (k < end) { arr[k++] = left[i++]; } }
2.3-3


证明 T(n) = nlgn ↓ 当 n = 2^1时,T(2) = 2 = 2 * lg2 成立, 假设当 n = 2^k 时,T(2^k) = 2^k * lg(2^k) = 2^k * k 成立, 当 n = 2^(k+1)时,T(2^(k+1)) = 2 * (2^k * k) + 2^(k+1) = 2^(k+1) * (k+1) 因此 T(n) = nlgn 成立。
2.3-4
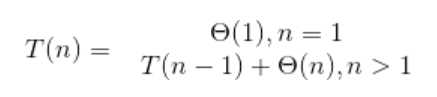
js代码:

class InsertSort { static sort(arr, start, end) { if (end - start > 1) { InsertSort.sort(arr, start, end - 1); let key = arr[end - 1]; let i = end - 2; // point to the number which 'key' prepare to compare while (i >= start && arr[i] > key) { arr[i + 1] = arr[i]; i--; } arr[i + 1] = key; } else { return; } } static run(data) { // convert a string to a numeric array data = CommonUtil.handleData(data); InsertSort.sort(data, 0, data.length); console.log(data); } }
2.3-5
js代码:
static find(x, arr, start, end) { if (start > end) return { success: false}; let mid = Math.floor((start + end) / 2); if (arr[mid] == x) { return { success: true, index: mid}; } else if (arr[mid] < x) { return BinarySearch.find(x, arr, mid + 1, end); } else { return BinarySearch.find(x, arr, start, mid - 1); } }
最坏情况就是找不到,二分查找的递归式:

根据书上的递归树得到总代价为clgn + c,因此最坏情况运行时间是theta lgn
2.3-6
换一种数据结构也许可以,采用数组做不到(查找位置lgn插入时间n,总时间还是n^2)。
附加:二叉搜索树(平均情况nlgn,最坏n^2) VS. 插入排序(n^2),两万数据实测↓
重复排序100次:
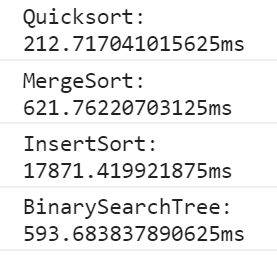
2.3-7
js代码描述:
class IntegerSum { static searchSum(arr, start, end, x) { if (end - start <= 1) return false; let sum = arr[start] + arr[end - 1]; if (sum < x) { return IntegerSum.searchSum(arr, start + 1, end, x); } else if (sum > x) { return IntegerSum.searchSum(arr, start, end - 1, x); } else { console.log(arr[start], arr[end - 1]); return true; } } static run(data) { data = CommonUtil.handleData(data); // cn MergeSort.sort(data, 0, data.length); // cnlgn // let x = Number(prompt("please enter the value of x :")); let x = Math.floor(Math.random() * 40); console.log("data=" + data); console.log("x=" + x); let end = -1; while (data[++end] <= x); // cn let result; let max = data[end - 1] + data[end - 2]; let min = data[0] + data[1]; if (max < x || min > x) { // deal with special situations result = false; } else if (max == x || min == x) { result = true; } else { result = IntegerSum.searchSum(data, 0, end, x); // cn } console.log(result); } }

