Google's Machine Learning Crash Course #03# Reducing Loss
Goal of training a model is to find a set of weights and biases that have low loss, on average, across all examples. —— Descending into ML: Training and Loss
注释:教程中的 loss ≠ 平均方差,而是指单个 labeled example 的方差(也就是误差 loss ),这里的 reducing loss 是指减小整体的误差(就是 MSE 了)
An Iterative Approach
我们的最终目的就得到一个较好的 model(假设 feature 只有一个,那么这个 model 很可能是一条直线),这个 model 可以比较准确地帮助我们推断、预测。
那么什么是比较好的 model 呢?具有总体低 loss 的 model 就是好的 model ,问题在于,如何计算总体 loss 以及怎样减小总体 loss 以逼近我们想要的 model ,在上一节已经谈到,我们经常用平均方差来判断一个 model 的好坏,平均方差大的就是总体 loss 大的,说明 model 不好,平均方差越趋近于零,则 model 越完美。
可以想象这样一个过程:
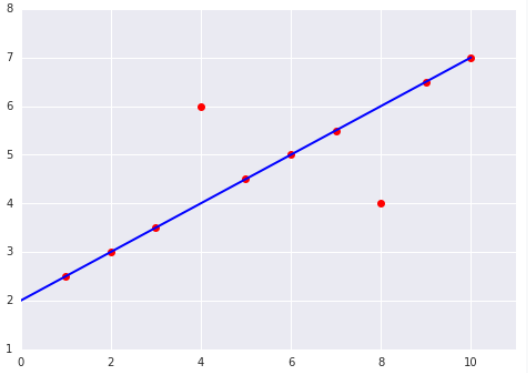
我们先随便画一条直线,然后计算它的 loss (假设已经一个这样的函数,例如 getLoss 什么的),上面 MSE算出来是 8 ,发现好大 ,这个时候我们微调直线的斜率 w 以及 y轴截距 b 得到一条新的直线,就像下面这样,MSE 是 4 ,发现更小了, 于是我们继续 ......
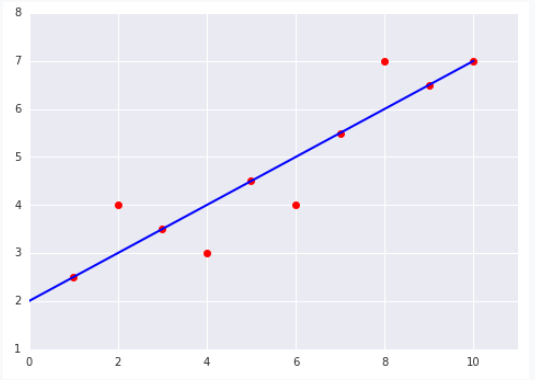
就这样循环往复: 微调斜率w 和截距b → 计算 loss → 微调斜率w 和截距b → 计算 loss → 微调斜率w 和截距b → ...
直到 loss 减小到几乎不再变化(术语叫做模型已经收敛),我们就成功了,整个过程可以用下面这张图描述:
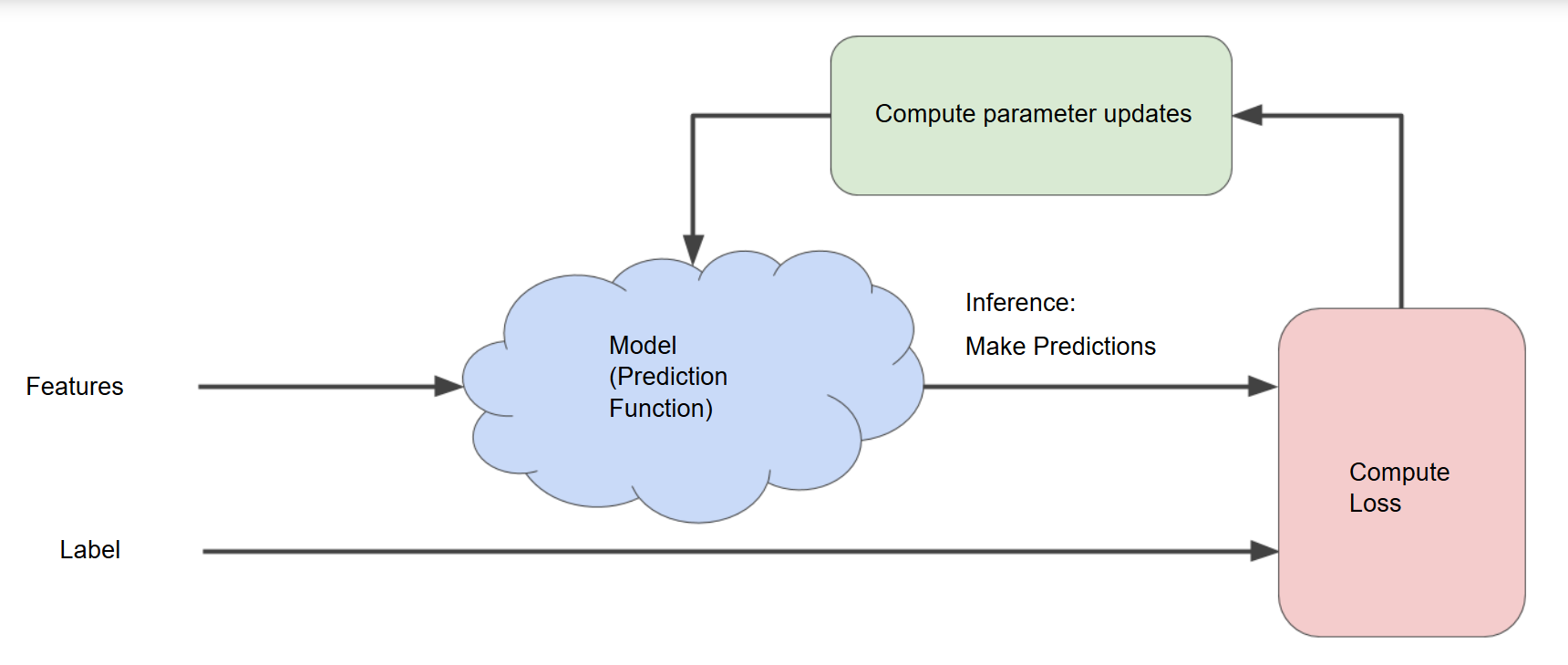
Gradient Descent
这一小节讲述具体如何“微调斜率w ”。
假设我们有足够的时间和计算资源对每一个w的可能取值计算 loss ,那么我们一定会得到一个这样的图像:
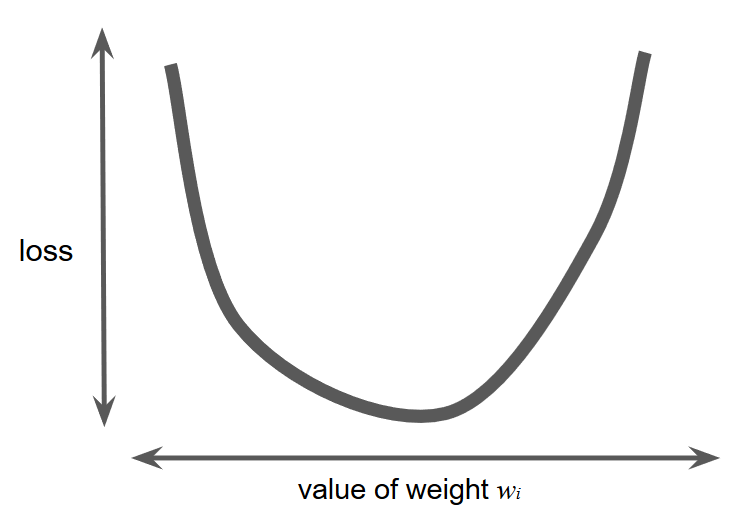
收敛问题只有一个最小值,就像图像上看到的,仅有一个地方的斜率为 0 .
如果我们真有那么多的时间和计算资源,像上面那样做就可以很直观、容易地得到最恰当的 w 了,不幸地是,现实中我们可没有那么多时间,“对每个可能的 w 在整个数据集上计算 loss ”这一做法效率太低了。有一种更好地方式来找最低点,它在机器学习中非常流行,叫“梯度下降法”。
这种方式的第一步是随机取一个点(随机定下一个 w),很多算法都直接取 0 ,取哪一点都是无关紧要的。
之后,梯度下降算法计算这一点的斜率(导数),如果有多个权重 w ,那么梯度就是这一点关于各个 w的偏导数构成的向量。
记住,梯度是一个向量,因此它具有方向和大小。因此,梯度下降算法朝着负梯度迈出一步(step),以便尽快的减少 loss . 它将梯度大小的一部分加到起点处得到下一个点,并不断重复上述步骤,越来越接近最小值。
Learning Rate
As noted, the gradient vector has both a direction and a magnitude. Gradient descent algorithms multiply the gradient by a scalar known as the learning rate (also sometimes called step size) to determine the next point. For example, if the gradient magnitude is 2.5 and the learning rate is 0.01, then the gradient descent algorithm will pick the next point 0.025 away from the previous point.
很多程序员都花费大量的时间调整学习速率,学习速率太小,那么整个学习过程会非常漫长,但是,如果学习速率太大,你甚至可能永远得不到最终的结果(点总是在最低点的两端来回弹跳)。
每一个回归问题都有一个比较恰当的学习速率,它取决于函数的平缓程度。如果你知道 loss-权重 函数的梯度很小,就可以放心地用大的学习速率尝试。(因为下一点的距离是学习速率 * 梯度,梯度小的话,学习速率大一点也无妨,并不容易因为前进太多而错过最低点)
PS. The Goldilocks learning rate 代表着最佳学习速率,实践中,找到完美的学习速率并非必要的,我们只需要找到一个“足够大又不过大”的学习速率就好了。
Stochastic Gradient Descent 随机梯度下降
full-batch iteration 每次迭代都用整个数据集
Stochastic gradient descent (SGD) 每次迭代随机仅仅选择 1 个 example
Mini-batch stochastic gradient descent (mini-batch SGD) 每次迭代随机选择 10 ~ 1000 个 example

 浙公网安备 33010602011771号
浙公网安备 33010602011771号