Google's Machine Learning Crash Course #02# Descending into ML
INDEX
How do we know if we have a good line
So as we said before, our model is something that we learned from data.
And there are lots of complicated model types and lots of interesting ways we can learn from data.
But we're gonna start with something very simple and familiar.
This will open the gateway to more sophisticated methods.
Let's train a first little model from data.
So here we've got a small data set.
On the X axis, we've got our input feature, which is showing housing square footage.
On our Y axis, we've got the target value that we're trying to predict of housing price.
So we're gonna try and create a model that takes in housing square footage as an input feature and predicts housing price as an output feature.
Here we've got lots of little labeled examples in our data set.
And I'm go ahead and channel our inner ninth grader to fit a line.
It can maybe take a look at our data set and fit a line that looks about right here. Maybe something like this.
And this line is now a model that predicts housing price given an input.
We can recall from algebra one that we can define this thing as Y = WX + B.
Now in high school algebra we would have said MX, here we say W because it's machine learning.
And this is referring to our weight vectors.
Now you'll notice that we've got a little subscript here because we might be in more than one dimension.
This B is a bias.
and the W gives us our slope.
How do we know if we have a good line?
Well, we might wanna think of some notion of loss here.
Loss is showing basically how well our line is doing at predicting any given example.
So we can define this loss by looking at the difference between the prediction for a given X value
and the true value for that example.
So this guy has some moderate size loss.
This guy has near-zero loss.
Here we've got exactly zero loss.
Here we probably have some positive loss.
Loss is always on a zero through positive scale.
How might we define loss? Well, that's something that we'll need to think about in a slightly more formal way.
So let's think about one convenient way to define loss for regression problems.
Not the only loss function, but one useful one to start out with.
We call this L2 loss, which is also known as squared error.
And it's a loss that's defined for an individual example by taking the square of the difference between our model's prediction and the true value.
Now obviously as we get further and further away from the true value, the loss that we suffer increases with a square.
Now, when we're training a model we don't care about minimizing loss on just one example, we care about minimizing loss across our entire data set.
Linear Regression
如何由 labeled examples 得到一个线性关系?(model)
假设我们要给温度(y)和蟋蟀每分钟的叫声(x)建立模型。可以这么做:
- 利用已有的数据作出散点图
- 画一条简单的直线近似两者的关系
- 利用直线的方程,写出线性表达式,例如 y = wx + b
这里的 y 就是我们试图预测的东西,w 是直线的坡度, b 是 y 轴的截距, x 是特征(feature)
如果想要预测一个尚未发生的情况,只需要把 feature 代入模型就可以了。一个复杂的模型依赖更多的 feature ,每个 feature 都有独立的权重:
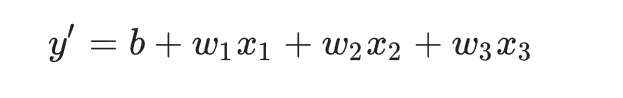
Training and Loss
训练一个模型仅仅意味着得到一条好的直线(这需要好的权重 w 和偏差 b)。
在监督学习中,机器学习算法检查很多的 example 并找到一个具有最小 loss 的模型,这个过程叫做 empirical risk minimization
loss 是一个数字,表明模型的预测在单个 example 上有多糟糕,如果模型的预测是完美的,那么 loss 为零; 否则,loss 更大。
训练模型的目标是找到一组对于整体数据而言、具有低 loss 的权重 w 和偏差 b 。
一种比较流行的计算 loss 的方式就是 squared loss (也被叫做L2 loss):
Mean square error (MSE) 是每个 example 的平均 squared loss
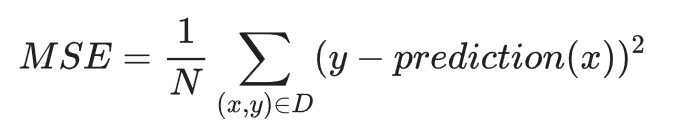
现在我们知道训练模型的目标了:找到具有低 loss 的直线,怎样才算低 loss 呢?平均方差最小的就是了,接下来的问题是,我们如何逼近这条直线?

 浙公网安备 33010602011771号
浙公网安备 33010602011771号