C++ 电路布线/最短路径问题

问题描述

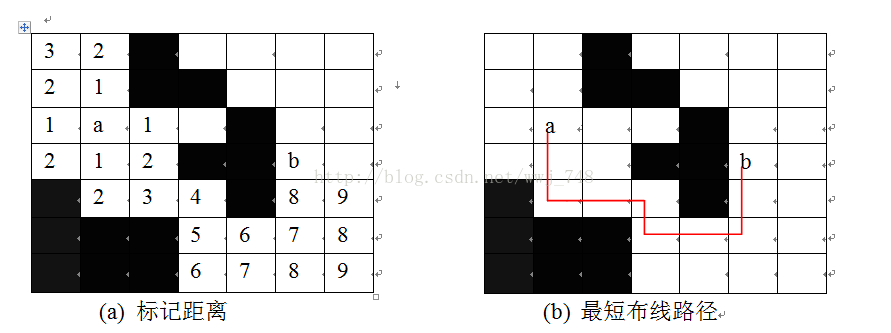
用二维数组表示地图，若值为 1 则表示有障碍物，若值为 0 则表示可以通行。

输入： m*n 的二维数组，布线起点坐标，布线终点坐标。

输出： 最短布线距离以及对应的布线路径。

 

问题分析

从起点开始布线，将起点标记为 0 ，把四周可布线的位置标记为 起点标记值 + 1 ，同时将这些点插进队列 Q （插到队尾）。

从 Q 中取出一个点（队首元素）重复布线动作，将可布线位置标记为 取出点标记值 + 1 ，并插进 Q 。不断重复上一个动作，直到找到终点，此时终点的标记值即最短布线距离。

为什么终点的标记值会等于最短布线距离呢？

事实上对于每一点这个结论都是成立的（某点的标记值=该点到起点的最短距离）。

（方块表示起点，椭圆表示终点）

在布线的过程中，始终遵循的规则是：标记值越小的越先布线。（越先入队的越先布线）

我们假设对于标记值为 n 的点该结论成立，我们只需要证明从标记值为 n 的点出发，找到的标记值为 n+1 的点确实最短就可以了。

我们考察标记值 n 周围的可布线点，可以分为两类：已布线点和未布线点。

对于未布线的点：由布线规则可知，所有标记值 < n 点都已经布线完毕，点未被布线的唯一原因是任何一个标记值 < n 的点都无法与它相邻（到不了或者需要付出更大的代价才能到），所以该点只能通过点 n 或者相邻的标记值同样为 n 的点与起点联通，从而取得最小值，故对标记值为 n+1 的点结论同样成立。

因此该结论对于任意标记值的点都成立。

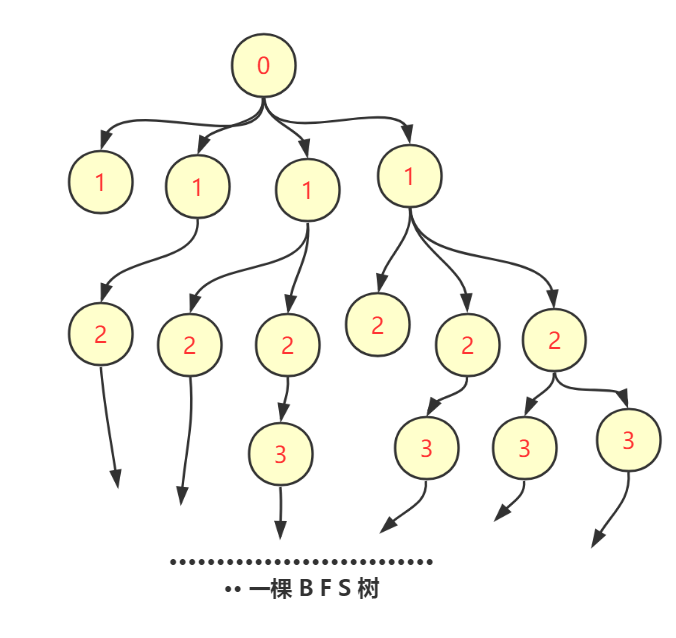
或者，一句话说就是迷宫格子形成了一颗BFS树，事实上我们已经把所有更短的路径都search出来了。所以不可能有更短的。

 

C++ 代码

#include <stdio.h>
#include <cstdlib>
#include <iostream>
#include <queue>
  
using namespace std;
#define MAX 6

struct Point {
    int x;
    int y;
    int len;
    Point* pre;

    Point(): len(0), pre(0) {}
    Point(int x, int y): x(x), y(y), len(0), pre(0) {}
    void setPoint(int x, int y) {
        this->x = x;
        this->y = y;
    }
};


queue<Point> mark;
void test(Point (*p)[MAX]);

bool work(Point& q, Point& e, int (*map)[MAX], Point (*p)[MAX]) {
    int x, y;
    // up 
    if ((x=q.x-1) >= 0 && map[x][y=q.y] != 1 && p[x][y].len == 0) {
        p[x][y].len = q.len + 1;
        p[x][y].pre = &q;
        if (x == e.x && y == e.y) {
            return true;
        } else {
            mark.push(p[x][y]);
        }
    }
    // down 
    if ((x=q.x+1) < MAX && map[x][y=q.y] != 1 && p[x][y].len == 0) {
        p[x][y].len = q.len + 1;
        p[x][y].pre = &q;
        if (x == e.x && y == e.y) {
            return true;
        } else {
            mark.push(p[x][y]);
        }
    }
    // left 
    if ((y=q.y-1) >= 0 && map[x=q.x][y] != 1 && p[x][y].len == 0) {
        p[x][y].len = q.len + 1;
        p[x][y].pre = &q;
        if (x == e.x && y == e.y) {
            return true;
        } else {
            mark.push(p[x][y]);
        }
    }
    // right 
    if ((y=q.y+1) < MAX && map[x=q.x][y] != 1 && p[x][y].len == 0) {
        p[x][y].len = q.len + 1;
        p[x][y].pre = &q;
        if (x == e.x && y == e.y) {
            return true;
        } else {
            mark.push(p[x][y]);
        }
    }
    return false;
}

void f(int (*map)[MAX], Point& s, Point& e, bool& k, Point (*p)[MAX]) {
    mark.push(s);
    int flag = false;
    while (mark.size() != 0 && !flag) { // 终止条件：找遍所有点都没找到终点&找到终点
        flag = work(mark.front(), e, map, p);
        mark.pop();
        test(p); // 输出布线情况
    }
    k = flag;
}

void test(Point (*p)[MAX]) { // 输出布线情况
    for (int i = 0; i != MAX; ++i) {
        for (int j = 0; j != MAX; ++j) {
            printf("%d ", p[i][j].len);
        }
        cout << endl;
    }    
    cout << endl;
}

void printPath(Point& end) {
    if (end.pre == 0) {
        printf("[%d][%d]\n", end.x, end.y);
        return;
    } else {
        printPath(*(end.pre));
        printf("[%d][%d]\n", end.x, end.y);
    }
}

int main()
{
    int map[MAX][MAX] = { 0, 0, 0, 0, 0, 1,
                          0, 0, 0, 0, 1, 0,
                          0, 0, 0, 0, 0, 1,
                          0, 0, 0, 1, 0, 1,
                          0, 1, 0, 0, 0, 0,
                          1, 1, 0, 1, 1, 1 };

    Point s(1, 1);
    Point e(4, 4);
    
    bool k = false;
    Point p[MAX][MAX];
    p[s.x][s.y].len = 1;
    for (int i = 0; i != MAX; ++i) {
        for (int j = 0; j != MAX; ++j) {
            p[i][j].setPoint(i, j);
        }
    } // 初始化
    
    f(map, s, e, k, p);
    if (k) {
        printf("MIN=%d\n", p[e.x][e.y].len);
        printPath(p[e.x][e.y]);
    } else {
        printf("ERROR\n"); // 起点与终点不连通
    }
    
    return 0;
}

 

附件：迷宫问题

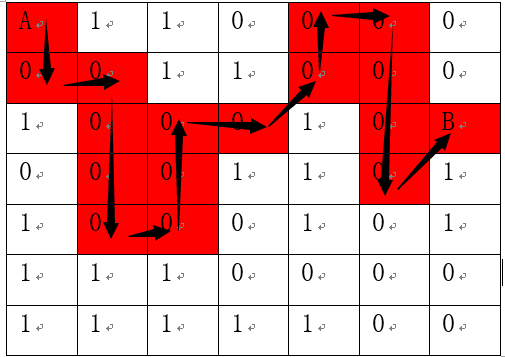
上面那道题用队列，这道用栈。

#include <stdio.h>
#define MAX 7

struct Point {
    int x;
    int y;
    bool mark;
    Point(): x(0), y(0), mark(false) {}
    Point(int x, int y): x(x), y(y) {}
    void setPosition(int x, int y) {
        this->x = x;
        this->y = y;
    }
};

Point p[MAX][MAX];
bool seekPath(int (*map)[MAX], Point& s, Point& e) {
    p[s.x][s.y].mark = true;
    if (s.x == e.x && s.y == e.y) {
        printf("MAP[%d][%d]\n", e.x, e.y);
        return true;
    }

    //printf("seekPath:1\n");
    if (s.x+1 < MAX && map[s.x+1][s.y] != 1 && !p[s.x+1][s.y].mark && seekPath(map, p[s.x+1][s.y], e)) {
            printf("MAP[%d][%d]\n", s.x, s.y);
            return true;
    }
    //printf("seekPath:2\n");
    if (s.x-1 >= 0 && map[s.x-1][s.y] != 1 && !p[s.x-1][s.y].mark && seekPath(map, p[s.x-1][s.y], e)) {
            printf("MAP[%d][%d]\n", s.x, s.y);
            return true;
    }
    //printf("seekPath:3\n");
    if (s.y+1 < MAX && map[s.x][s.y+1] != 1 && !p[s.x][s.y+1].mark && seekPath(map, p[s.x][s.y+1], e)) {
            printf("MAP[%d][%d]\n", s.x, s.y);
            return true;
    }
    //printf("seekPath:4\n");
    if (s.y-1 >= 0 && map[s.x][s.y-1] != 1 && !p[s.x][s.y-1].mark && seekPath(map, p[s.x][s.y-1], e)) {
            printf("MAP[%d][%d]\n", s.x, s.y);
            return true;
    }
    //printf("seekPath:5\n");
    if (s.x+1 < MAX && s.y+1 < MAX && map[s.x+1][s.y+1] != 1 && !p[s.x+1][s.y+1].mark && seekPath(map, p[s.x+1][s.y+1], e)) {
            printf("MAP[%d][%d]\n", s.x, s.y);
            return true;
    }
    //printf("seekPath:6\n");
    if (s.x+1 < MAX && s.y-1 >= 0 && map[s.x+1][s.y-1] != 1 && !p[s.x+1][s.y-1].mark && seekPath(map, p[s.x+1][s.y-1], e)) {
            printf("MAP[%d][%d]\n", s.x, s.y);
            return true;
    }
    //printf("seekPath:7\n");
    if (s.x-1 >= 0 && s.y+1 < MAX && map[s.x-1][s.y+1] != 1 && !p[s.x-1][s.y+1].mark && seekPath(map, p[s.x-1][s.y+1], e)) {
            printf("MAP[%d][%d]\n", s.x, s.y);
            return true;
    }
    //printf("seekPath:8\n");
    if (s.x-1 >= 0 && s.y-1 >= 0 && map[s.x-1][s.y-1] != 1 && !p[s.x-1][s.y-1].mark && seekPath(map, p[s.x-1][s.y-1], e)) {
            printf("MAP[%d][%d]\n", s.x, s.y);
            return true;
    }
    return false;
}

void f(int (*map)[MAX], Point& s, Point& e) {
    // chushihua
    for (int i = 0; i != MAX; ++i) {
        for (int j = 0; j != MAX; ++j) {
            p[i][j].setPosition(i, j);
        }
    }

    // work
    if (!seekPath(map, s, e)) {
        printf("ERROR!\n");
    }
    //printf("f:runnable\n");
}

int main()
{
    int map[MAX][MAX] = { 0, 1,    1, 0, 0, 0,    0,
                          0, 0, 1, 1, 0, 0, 0,
                          1, 0, 0, 0, 1, 0, 0,
                          0, 0, 0, 1, 1, 0, 1,
                          1, 0, 0, 0, 1, 0, 1,
                          1, 1, 1, 0, 0, 0, 0,
                          1, 1, 1, 1, 1, 0, 0 };
    Point s(0, 0);
    Point e(2, 6);    
    f(map, s, e);
    //printf("main:runnable\n");
    return 0;
}

留着备用。