线代笔记 #09# 点积(标量积、数量积、内积)
饮水思源:线性代数的本质 - 点积与对偶性
概念
向量间的一种运算。
用途
通过这种运算可以检验两个向量的指向是否相同(计算结果为正则相同,负则不同)。
内积与顺序无关
用对称性解释。就是先假设两向量是等长的(关于某条直线对称),那么就无所谓谁投影都谁上面。然后去改变其中一个向量大小的比例,发现其改变的比例会如实地反映到内积值上。例如,将其中一个向量的大小放大2倍,结果内积值也会放大2倍,这一点并不会因为谁投影到谁上面而改变,所以,内积与顺序无关。
对偶性
1 * n 的矩阵和 n 维向量间存在着某种神奇的联系。
每当你看到某个从 n 维空间到 1 维数轴的线性变换
就一定可以在那个 n 维空间中找到唯一的一个 n 维向量(称作这个变换的对偶向量,并且,形式上看,表示线性变换的那个矩阵和那个 n 维向量恰好就是转置的关系),使得
对该空间下另一 n 维向量应用此线性变换的计算结果与
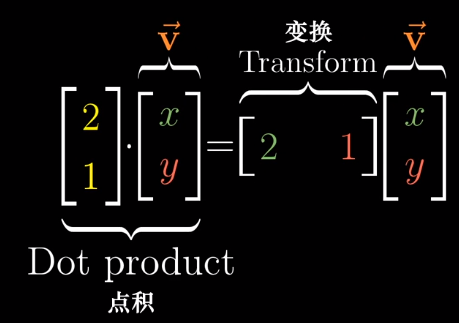
和对应的对偶向量进行点乘的计算结果一致。如下图所示