Craking the Interview-1
1.6
90度旋转NxN矩阵
Given an image represented by an NxN matrix, where each pixel in the image is 4 bytes, write a method to rotate the image by 90 degrees. Can you do this in place?
SOLUTION
The rotation can be performed in layers, where you perform a cyclic swap on the edges on each layer. In the first for loop, we rotate the first layer (outermost edges). We rotate the edges by doing a four-way swap first on the corners, then on the element clockwise from the edges, then on the element three steps away. Once the exterior elements are rotated, we then rotate the interior region’s edges.
Java代码:
package Question1_6; import CareerCupLibrary.*; public class Question { public static void rotate(int[][] matrix, int n) { for (int layer = 0; layer < n / 2; ++layer) { int first = layer; int last = n - 1 - layer; for(int i = first; i < last; ++i) { int offset = i - first; int top = matrix[first][i]; // save top // left -> top matrix[first][i] = matrix[last-offset][first]; // bottom -> left matrix[last-offset][first] = matrix[last][last - offset]; // right -> bottom matrix[last][last - offset] = matrix[i][last]; // top -> right matrix[i][last] = top; // right <- saved top } } } public static void main(String[] args) { int[][] matrix = AssortedMethods.randomMatrix(10, 10, 0, 9); AssortedMethods.printMatrix(matrix); rotate(matrix, 10); System.out.println(); AssortedMethods.printMatrix(matrix); } }
C++代码:
template <class T> void matrix_rotate(T**M,int N){ if(M==0||N<=0) return ; for(int k=0;k<N/2;k++){ for(int i=k;i<N-1-k;i++){ T top=M[k][i]; M[k][i]=M[N-1-i][k]; M[N-1-i][k]=M[N-1-k][N-1-i]; M[N-1-k][N-1-i]=M[i][N-1-k]; M[i][N-1-k]=top; } } } template <class T> T**matrix_alloc(int r,int c){ if(r<=0||c<=0) return 0; int header=r*sizeof(T*); int data=r*c*sizeof(T); T** rbuf=(T**)malloc(header+data); T* dbuf=(T*)(rbuf+r); for(int i=0;i<r;i++){ rbuf[i]=(T*)(dbuf+i*c); } return rbuf; } template <class T> void matrix_print(T**M,int r,int c){ for(int i=0;i<r;i++){ for(int j=0;j<c;j++) cout<<M[i][j]<<' '; cout<<endl; } } int main(){ int N=4; char** M=matrix_alloc<char>(N,N); for(int i=0;i<N;i++) for(int j=0;j<N;j++){ M[i][j]='A'+i*N+j; } matrix_print(M,N,N); matrix_rotate(M,N); cout<<"================"<<endl; matrix_print(M,N,N); free(M); }
1.7
如果矩阵的一个值为0, 那么就将其所在行和列的所有值都置为0
Write an algorithm such that if an element in an MxN matrix is 0, its entire row and column is set to 0.
SOLUTION
At first glance, this problem seems easy: just iterate through the matrix and every time we see a 0, set that row and column to 0. There’s one problem with that solution though: we will “recognize” those 0s later on in our iteration and then set their row and column to zero. Pretty soon, our entire matrix is 0s!
One way around this is to keep a second matrix which flags the 0 locations. We would then do a second pass through the matrix to set the zeros. This would take O(MN) space. Do we really need O(MN) space? No. Since we’re going to set the entire row and column to zero, do we really need to track which cell in a row is zero? No. We only need to know that row 2, for example, has a zero.
The code below implement this algorithm. We keep track in two arrays all the rows with zeros and all the columns with zeros. We then make a second pass of the matrix and set a cell to zero if its row or column is zero.
C++代码如下:
void matrix_setZeros(int**M,int r,int c){ if(M==0||r<=0||c<=0) return; int *row=new int[r](); int *col=new int[c](); for(int i=0;i<r;i++){ for(int j=0;j<c;j++) { if(M[i][j]==0) row[i]=1,col[j]=1; } } for(int i=0;i<r;i++){ if(row[i]==1){ for(int j=0;j<c;j++) M[i][j]=0; } } for(int j=0;j<c;j++) if(col[j]==1) for(int i=0;i<r;i++) M[i][j]=0; delete[] row; delete[] col; } int main(){ int r=5,c=4; int **M=matrix_alloc<int>(r,c); for(int i=0;i<r;i++) for(int j=0;j<c;j++){ int t=rand()%10; M[i][j]=t; } matrix_print(M,r,c); cout<<"=============\n"; matrix_setZeros(M,r,c); matrix_print(M,r,c); free(M); }
2.1
删除链表中重复的元素
Write code to remove duplicates from an unsorted linked list.
FOLLOW UP
How would you solve this problem if a temporary buffer is not allowed?
SOLUTION
If we can use a buffer, we can keep track of elements in a hashtable and remove any dups:
Without a buffer, we can iterate with two pointers: “current” does a normal iteration, while “runner” iterates through all prior nodes to check for dups. Runner will only see one dup per node, because if there were multiple duplicates they would have been removed already.
Java代码:
public class Question { public static void deleteDups(LinkedListNode n) { Hashtable table = new Hashtable(); LinkedListNode previous = null; while (n != null) { if (table.containsKey(n.data)) { previous.next = n.next; } else { table.put(n.data, true); previous = n; } n = n.next; } } public static void deleteDups2(LinkedListNode head) { if (head == null) return; LinkedListNode previous = head; LinkedListNode current = previous.next; while (current != null) { // Look backwards for dups, and remove any that you see. LinkedListNode runner = head; while (runner != current) { if (runner.data == current.data) { LinkedListNode tmp = current.next; previous.next = tmp; current = tmp; /* We know we cant have more than one dup preceding * our element since it would have been removed * earlier. */ break; } runner = runner.next; } /* If runner == current, then we didnt find any duplicate * elements in the previous for loop. We then need to * increment current. * If runner != current, then we must have hit the break * condition, in which case we found a dup and current has * already been incremented.*/ if (runner == current) { previous = current; current = current.next; } } } public static void main(String[] args) { LinkedListNode head = AssortedMethods.randomLinkedList(10, 0, 10); System.out.println(head.printForward()); deleteDups2(head); System.out.println(head.printForward()); } }
2.4
You have two numbers represented by a linked list, where each node contains a single digit. The digits are stored in reverse order, such that the 1’s digit is at the head of the list. Write a function that adds the two numbers and returns the sum as a linked list.
EXAMPLE
Input: (3 -> 1 -> 5), (5 -> 9 -> 2)
Output: 8 -> 0 -> 8
SOLUTION
We can implement this recursively by adding node by node, just as we would digit by digit.
1. result.data = (node1 + node2 + any earlier carry) % 10
2. if node1 + node2 > 10, then carry a 1 to the next addition.
3. add the tails of the two nodes, passing along the carry.
Java 代码如下:
public class Question { private static LinkedListNode addLists(LinkedListNode l1, LinkedListNode l2, int carry) { LinkedListNode result = new LinkedListNode(carry, null, null); int value = carry; if (l1 != null) { value += l1.data; } if (l2 != null) { value += l2.data; } result.data = value % 10; if (l1 != null || l2 != null || value >= 10) { LinkedListNode more = addLists(l1 == null ? null : l1.next, l2 == null ? null : l2.next, value >= 10 ? 1 : 0); result.setNext(more); } return result; } public static int linkedListToInt(LinkedListNode node) { int value = 0; if (node.next != null) { value = 10 * linkedListToInt(node.next); } return value + node.data; } public static void main(String[] args) { LinkedListNode list1 = AssortedMethods.randomLinkedList(5, 0, 9); LinkedListNode list2 = AssortedMethods.randomLinkedList(5, 0, 9); LinkedListNode list3 = addLists(list1, list2, 0); System.out.println(" " + list1.printForward()); System.out.println("+ " + list2.printForward()); System.out.println("= " + list3.printForward()); int l1 = linkedListToInt(list1); int l2 = linkedListToInt(list2); int l3 = linkedListToInt(list3); System.out.print(l1 + " + " + l2 + " = " + l3 + "\n"); System.out.print(l1 + " + " + l2 + " = " + (l1 + l2)); } }
2.5
判断链表中是否存在环, 并且找到环的开始点
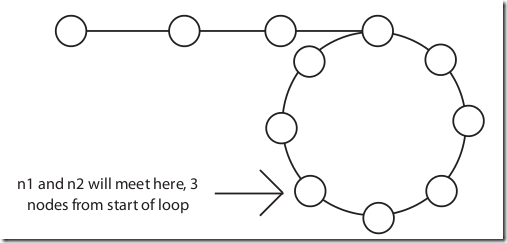
Given a circular linked list, implement an algorithm which returns node at the beginning of the loop.
DEFINITION
Circular linked list: A (corrupt) linked list in which a node’s next pointer points to an earlier node, so as to make a loop in the linked list.
EXAMPLE
Input: A -> B -> C -> D -> E -> C [the same C as earlier]
Output: C
SOLUTION
If we move two pointers, one with speed 1 and another with speed 2, they will end up meet- ing if the linked list has a loop. Why? Think about two cars driving on a track—the faster car will always pass the slower one! The tricky part here is finding the start of the loop. Imagine, as an analogy, two people racing around a track, one running twice as fast as the other. If they start off at the same place, when will they next meet? They will next meet at the start of the next lap.
Now, let’s suppose Fast Runner had a head start of k meters on an n step lap. When will they next meet? They will meet k meters before the start of the next lap. (Why? Fast Runner would have made k + 2(n - k) steps, including its head start, and Slow Runner would have made n - k steps. Both will be k steps before the start of the loop.)
Now, going back to the problem, when Fast Runner (n2) and Slow Runner (n1) are moving around our circular linked list, n2 will have a head start on the loop when n1 enters. Specifically, it will have a head start of k, where k is the number of nodes before the loop. Since n2 has a head start of k nodes, n1 and n2 will meet k nodes before the start of the loop.
So, we now know the following:
1. Head is k nodes from LoopStart (by definition).
2. MeetingPoint for n1 and n2 is k nodes from LoopStart (as shown above).
Thus, if we move n1 back to Head and keep n2 at MeetingPoint, and move them both at the same pace, they will meet at LoopStart.
C++代码如下:
struct node{ int data; node* next; }; node* lnklist_create(int* arr,int N){ if(arr==0||N<=0) return 0; node* head=new node; head->data=arr[0]; node* p=head; for(int i=1;i<N;i++) { node* t=new node; t->data=arr[i]; p->next=t; p=t; } p->next=0; return head; } void lnklist_destroy(node* head){ while(head!=0){ node* t=head; head=head->next; delete t; } } template <class T> void arr_print(T* arr,int N){ if(arr==0||N<=0) return; for(int i=0;i<N;i++) cout<<arr[i]<<' '; cout<<endl; } template <class T> void lnklist_print(node* head){ while(head!=0) { cout<<head->data<<' '; head=head->next; } cout<<endl; } node* find_beginning(node* head){ if(head==0) return 0; node* p1,*p2; p1=head,p2=head; while(p2->next!=0){ p1=p1->next; p2=p2->next->next; if(p1==p2) break; } if(p2->next==0) return 0; p1=head; while(p1!=p2){ p1=p1->next; p2=p2->next; } return p2; } int main(){ const int N=10; int arr[N]; for(int i=0;i<N;i++) arr[i]=rand()%100; arr_print(arr,N); node* head=lnklist_create(arr,N); node* p=head; while(p->next!=0) p=p->next; p->next=head->next->next->next; printf("%d %p\n",p->next->data,p->next); node* q=find_beginning(head); printf("%d %p\n",q->data,q); p->next=0; lnklist_destroy(head); }
3.1
利用一个数组去实现3个栈.
Describe how you could use a single array to implement three stacks.
SOLUTION
Approach 1:
将数组划分为大小相等的三块, 分别给3个栈去使用
Divide the array in three equal parts and allow the individual stack to grow in that limited space (note: “[“ means inclusive, while “(“ means exclusive of the end point).
»» for stack 1, we will use [0, n/3)
»» for stack 2, we will use [n/3, 2n/3)
»» for stack 3, we will use [2n/3, n)
This solution is based on the assumption that we do not have any extra information about the usage of space by individual stacks and that we can’t either modify or use any extra space. With these constraints, we are left with no other choice but to divide equally.
Approach 2:
In this approach, any stack can grow as long as there is any free space in the array. We sequentially allocate space to the stacks and we link new blocks to the previous block. This means any new element in a stack keeps a pointer to the previous top element of that particular stack.
In this implementation, we face a problem of unused space. For example, if a stack deletes some of its elements, the deleted elements may not necessarily appear at the end of the array. So, in that case, we would not be able to use those newly freed spaces.
To overcome this deficiency, we can maintain a free list and the whole array space would be given initially to the free list. For every insertion, we would delete an entry from the free list.
In case of deletion, we would simply add the index of the free cell to the free list. In this implementation we would be able to have flexibility in terms of variable space utilization but we would need to increase the space complexity.
方案2的C++代码如下:
const int stackSize=300; int stackNum[3]={-1,-1,-1}; struct stackNode{ int value; int prev; stackNode(int v=0,int p=-1):value(v),prev(p){} }; stackNode buff[3*stackSize]; int indx_used=0; bool isFull(int no=0){ return indx_used==3*stackSize; } bool isEmpty(int no){ return stackNum[no]==-1; } void push(int no,int value){ if(no<0||no>2) return; if(indx_used==3*stackSize) return; int prev=stackNum[no]; buff[indx_used]=stackNode(value,prev); stackNum[no]=indx_used; indx_used++; } void pop(int no){ if(no<0||no>2) return; if(stackNum[no]==-1) return; int inx=stackNum[no]; stackNum[no]=buff[inx].prev; buff[inx]=buff[indx_used]; indx_used--; } int top(int no){ if(no<0||no>2||stackNum[no]==-1) exit(-1); return buff[stackNum[no]].value; } int main(){ int N=20; for(int i=0;i<N;i++){ int t=rand()%100; push(t%3,t); } cout<<stackNum[0]<<' ' <<stackNum[1]<<' ' <<stackNum[2]<<endl; for(int i=0;i<N;i++){ cout<<'<'<<buff[i].value<<',' <<buff[i].prev<<"> "; } cout<<endl; }
3.6
对栈进行升序排列
Write a program to sort a stack in ascending order. You should not make any assumptions about how the stack is implemented. The following are the only functions that should be used to write this program: push | pop | peek | isEmpty.
SOLUTION
Sorting can be performed with one more stack. The idea is to pull an item from the original stack and push it on the other stack. If pushing this item would violate the sort order of the new stack, we need to remove enough items from it so that it’s possible to push the new item. Since the items we removed are on the original stack, we’re back where we started. The algorithm is O(N^2) and appears below.
C++代码如下:
template <class T> void stack_sort(stack<T>& s1){ stack<T> s2; while(!s1.empty()) { T t=s1.top(); s1.pop(); while(!s2.empty()&&t>s2.top()){ s1.push(s2.top()); s2.pop(); } s2.push(t); } s1=s2; } int main(){ const int N=20; stack<int> s; for(int i=0;i<N;i++){ int v=rand()%100; s.push(v); cout<<v<<' '; } cout<<endl; stack_sort(s); while(!s.empty()) cout<<s.top()<<' ',s.pop(); cout<<endl; }
4.3
利用一个排序(升序)数组构建一个二叉树, 该二叉树具有最小的高度.
Given a sorted (increasing order) array, write an algorithm to create a binary tree with minimal height.
SOLUTION
We will try to create a binary tree such that for each node, the number of nodes in the left subtree and the right subtree are equal, if possible.
Algorithm:
1. Insert into the tree the middle element of the array.
2. Insert (into the left subtree) the left subarray elements
3. Insert (into the right subtree) the right subarray elements
4. Recurse
Java代码如下:
private static TreeNode addToTree(int arr[], int start, int end){ if (end < start) { return null; } int mid = (start + end) / 2; TreeNode n = new TreeNode(arr[mid]); n.setLeftChild(addToTree(arr, start, mid - 1)); n.setRightChild(addToTree(arr, mid + 1, end)); return n; } public static TreeNode createMinimalBST(int array[]) { return addToTree(array, 0, array.length - 1); }
4.4
给定一个二叉树, 为其每个高度的节点创建一个链表.
Given a binary search tree, design an algorithm which creates a linked list of all the nodes at each depth (eg, if you have a tree with depth D, you’ll have D linked lists).
SOLUTION
We can do a simple level by level traversal of the tree, with a slight modification of the breath-first traversal of the tree.
In a usual breath first search traversal, we simply traverse the nodes without caring which level we are on. In this case, it is critical to know the level. We thus use a dummy node to indicate when we have finished one level and are starting on the next.
Java代码如下:
public class Question { public static ArrayList<LinkedList<TreeNode>> findLevelLinkList(TreeNode root) { int level = 0; ArrayList<LinkedList<TreeNode>> result = new ArrayList<LinkedList<TreeNode>>(); LinkedList<TreeNode> list = new LinkedList<TreeNode>(); list.add(root); result.add(level, list); while (true) { list = new LinkedList<TreeNode>(); for(int i = 0; i < result.get(level).size(); i++){ TreeNode n = (TreeNode) result.get(level).get(i); if(n != null) { if(n.left != null) list.add(n.left); if(n.right!= null) list.add(n.right); } } if (list.size() > 0) { result.add(level + 1, list); } else { break; } level++; } return result; } public static void printResult(ArrayList<LinkedList<TreeNode>> result){ int depth = 0; for(LinkedList<TreeNode> entry : result) { Iterator<TreeNode> i = entry.listIterator(); System.out.print("Link list at depth " + depth + ":"); while(i.hasNext()){ System.out.print(" " + ((TreeNode)i.next()).data); } System.out.println(); depth++; } } public static void main(String[] args) { int[] nodes_flattened = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; TreeNode root = AssortedMethods.createTreeFromArray(nodes_flattened); ArrayList<LinkedList<TreeNode>> list = findLevelLinkList(root); printResult(list); } }
4.5
查找出二叉排序树的中序遍历的下一个节点.
Write an algorithm to find the ‘next’ node (e.g., in-order successor) of a given node in a binary search tree where each node has a link to its parent.
SOLUTION
We approach this problem by thinking very, very carefully about what happens on an in-order traversal. On an in-order traversal, we visit X.left, then X, then X.right.
So, if we want to find X.successor(), we do the following:
1. If X has a right child, then the successor must be on the right side of X (because of the order in which we visit nodes). Specifically, the left-most child must be the first node visited in that subtree.
2. Else, we go to X’s parent (call it P).
2.a. If X was a left child (P.left = X), then P is the successor of X
2.b. If X was a right child (P.right = X), then we have fully visited P, so we call successor(P).
Java代码如下:
public class Question { public static TreeNode inorderSucc(TreeNode e) { if (e != null) { TreeNode p; // Found right children -> return 1st inorder node on right if (e.parent == null || e.right != null) { p = leftMostChild(e.right); } else { // Go up until we抮e on left instead of right (case 2b) while ((p = e.parent) != null) { if (p.left == e) { break; } e = p; } } return p; } return null; } public static TreeNode leftMostChild(TreeNode e) { if (e == null) return null; while (e.left != null) e = e.left; return e; } public static void main(String[] args) { int[] array = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; TreeNode root = TreeNode.createMinimalBST(array); for (int i = 0; i < array.length; i++) { TreeNode node = root.find(array[i]); TreeNode next = inorderSucc(node); if (next != null) { System.out.println(node.data + "->" + next.data); } else { System.out.println(node.data + "->" + null); } } } }
4.7
判断T1是否为T2的子树
You have two very large binary trees: T1, with millions of nodes, and T2, with hundreds of nodes. Create an algorithm to decide if T2 is a subtree of T1.
SOLUTION
Note that the problem here specifies that T1 has millions of nodes—this means that we should be careful of how much space we use. Let’s say, for example, T1 has 10 million nodes—this means that the data alone is about 40 mb. We could create a string representing the inorder and preorder traversals. If T2’s preorder traversal is a substring of T1’s preorder traversal, and T2’s inorder traversal is a substring of T1’s inorder traversal, then T2 is a sub- string of T1. We can check this using a suffix tree. However, we may hit memory limitations because suffix trees are extremely memory intensive. If this become an issue, we can use an alternative approach.
Alternative Approach: The treeMatch procedure visits each node in the small tree at most once and is called no more than once per node of the large tree. Worst case runtime is at most O(n * m), where n and m are the sizes of trees T1 and T2, respectively. If k is the number of occurrences of T2’s root in T1, the worst case runtime can be characterized as O(n + k * m).
Java代码如下:
public class Question { public static boolean containsTree(TreeNode t1, TreeNode t2) { if (t2 == null) return true; // The empty tree is a subtree of every tree. else return subTree(t1, t2); } /* Checks if the binary tree rooted at r1 contains the binary tree * rooted at r2 as a subtree somewhere within it. */ public static boolean subTree(TreeNode r1, TreeNode r2) { if (r1 == null) return false; // big tree empty & subtree still not found. if (r1.data == r2.data) { if (matchTree(r1,r2)) return true; } return (subTree(r1.left, r2) || subTree(r1.right, r2)); } /* Checks if the binary tree rooted at r1 contains the * binary tree rooted at r2 as a subtree starting at r1. */ public static boolean matchTree(TreeNode r1, TreeNode r2) { if (r2 == null && r1 == null) return true; // nothing left in the subtree if (r1 == null || r2 == null) return false; // big tree empty & subtree still not found if (r1.data != r2.data) return false; // data doesn抰 match return (matchTree(r1.left, r2.left) && matchTree(r1.right, r2.right)); } public static void main(String[] args) { // t2 is a subtree of t1 int[] array1 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}; int[] array2 = {2, 4, 5, 8, 9, 10, 11}; TreeNode t1 = AssortedMethods.createTreeFromArray(array1); TreeNode t2 = AssortedMethods.createTreeFromArray(array2); if (containsTree(t1, t2)) System.out.println("t2 is a subtree of t1"); else System.out.println("t2 is not a subtree of t1"); // t4 is not a subtree of t3 int[] array3 = {1, 2, 3}; TreeNode t3 = AssortedMethods.createTreeFromArray(array1); TreeNode t4 = AssortedMethods.createTreeFromArray(array3); if (containsTree(t3, t4)) System.out.println("t4 is a subtree of t3"); else System.out.println("t4 is not a subtree of t3"); } }
4.8
打印出节点之和为某一个值的路径
You are given a binary tree in which each node contains a value. Design an algorithm to print all paths which sum up to that value. Note that it can be any path in the tree - it does not have to start at the root.
SOLUTION
Let’s approach this problem by simplifying it. What if the path had to start at the root? In that case, we would have a much easier problem: Start from the root and branch left and right, computing the sum thus far on each path.
When we find the sum, we print the current path. Note that we don’t stop just because we found the sum. Why? Because we could have the following path (assume we are looking for the sum 5): 2 + 3 + –4 + 3 + 1 + 2. If we stopped once we hit 2 + 3, we’d miss several paths (2 + 3 + -4 + 3 + 1 and 3 + -4 + 3 + 1 + 2). So, we keep going along every possible path.
Now, what if the path can start anywhere? In that case, we make a small modification. On every node, we look “up” to see if we’ve found the sum. That is—rather than asking “does this node start a path with the sum?,” we ask “does this node complete a path with the sum?”
What is the time complexity of this algorithm? Well, if a node is at level r, we do r amount of work (that’s in the looking “up” step). We can take a guess at O(n lg n) (n nodes, doing an average of lg n amount of work on each step), or we can be super mathematical:
There are 2^r nodes at level r.
1*2^1 + 2*2^2 + 3*2^3 + 4*2^4 + ... d * 2^d = sum(r * 2^r, r from 0 to depth)
= 2 (d-1) * 2^d + 2
n = 2^d ==> d = lg n
NOTE: 2^lg(x) = x
O(2 (lg n - 1) * 2^(lg n) + 2) = O(2 (lg n - 1) * n ) = O(n lg n)
Following similar logic, our space complexity is O(n lg n).
Java代码如下:
public class Question { public static void findSum(TreeNode head, int sum, ArrayList<Integer> buffer, int level) { if (head == null) { return; } int tmp = sum; buffer.add(head.data); for (int i = level;i >- 1; i--){ tmp -= buffer.get(i); if (tmp == 0) { print(buffer, i, level); } } ArrayList<Integer> c1 = (ArrayList<Integer>) buffer.clone(); ArrayList<Integer> c2 = (ArrayList<Integer>) buffer.clone(); findSum(head.left, sum, c1, level + 1); findSum(head.right, sum, c2, level + 1); } private static void print(ArrayList<Integer> buffer, int level, int i2) { for (int i = level; i <= i2; i++) { System.out.print(buffer.get(i) + " "); } System.out.println(); } public static void main(String [] args){ TreeNode root = new TreeNode(5); root.left = new TreeNode(3); root.right = new TreeNode(1); root.left.left = new TreeNode(4); root.left.right = new TreeNode(8); root.right.left = new TreeNode(2); root.right.right = new TreeNode(6); findSum(root, 8, new ArrayList<Integer>(), 0); } }
5.1
将N中的某些位设置为M
You are given two 32-bit numbers, N and M, and two bit positions, i and j. Write a method to set all bits between i and j in N equal to M (e.g., M becomes a substring of N located at i and starting at j).
EXAMPLE:
Input: N = 10000000000, M = 10101, i = 2, j = 6
Output: N = 10001010100
SOLUTION
This code operates by clearing all bits in N between position i and j, and then ORing to put M in there.
Java 代码如下:
public class Question { public static int updateBits(int n, int m, int i, int j) { int max = ~0; /* All 1抯 */ // 1抯 through position j, then 0抯 int left = max - ((1 << j) - 1); // 1抯 after position i int right = ((1 << i) - 1); // 1抯, with 0s between i and j int mask = left | right; // Clear i through j, then put m in there return (n & mask) | (m << i); } public static void main(String[] args) { int a = 103217; System.out.println(AssortedMethods.toFullBinaryString(a)); int b = 13; System.out.println(AssortedMethods.toFullBinaryString(b)); int c = updateBits(a, b, 4, 7); System.out.println(AssortedMethods.toFullBinaryString(c)); } }
5.3
Given an integer, print the next smallest and next largest number that have the same number of 1 bits in their binary representation.
SOLUTION
The Brute Force Approach:
An easy approach is simply brute force: count the number of 1’s in n, and then increment (or decrement) until you find a number with the same number of 1’s. Easy - but not terribly interesting. Can we do something a bit more optimal? Yes!
Number Properties Approach for Next Number
Observations:
»» If we “turn on” a 0, we need to “turn off” a 1
»» If we turn on a 0 at bit i and turn off a 1 at bit j, the number changes by 2^i - 2^j.
»» If we want to get a bigger number with the same number of 1s and 0s, i must be bigger than j.
Solution:
1. Traverse from right to left. Once we’ve passed a 1, turn on the next 0. We’ve now increased the number by 2^i. Yikes! Example: xxxxx011100 becomes xxxxx111100
2. Turn off the one that’s just to the right side of that. We’re now bigger by 2^i - 2^(i-1)
Example: xxxxx111100 becomes xxxxx101100
3. Make the number as small as possible by rearranging all the 1s to be as far right as possible: Example: xxxxx101100 becomes xxxxx100011
To get the previous number, we do the reverse.
1. Traverse from right to left. Once we’ve passed a zero, turn off the next 1. Example: xxxxx100011 becomes xxxxx000011.
2. Turn on the 0 that is directly to the right. Example: xxxxx000011 becomes xxxxx010011.
3. Make the number as big as possible by shifting all the ones as far to the left as possible. Example: xxxxx010011 becomes xxxxx011100 .
And now, for the code. Note the emphasis on pulling common code out into a reusable function. Your interviewer will look for “clean code” like this.
C++代码:
int get_bit(int n,int pos){ return (n&(1<<pos)); } void set_bit0(int& n,int pos){ n&=(~(1<<pos)); } void set_bit1(int& n,int pos){ n|=(1<<pos); } int get_nextNP(int n){ int pos=0; int cnt=0; while(!get_bit(n,pos)) pos++; while(get_bit(n,pos)) pos++,cnt++; set_bit1(n,pos); pos--; set_bit0(n,pos); cnt--; for(int i=pos-1;i>=cnt;i--) set_bit0(n,i); for(int i=cnt-1;i>=0;i--) set_bit1(n,i); return n; } int get_prevNP(int n){ int pos=0; int cnt=0; while(get_bit(n,pos)) pos++; while(!get_bit(n,pos)) pos++,cnt++; set_bit0(n,pos); pos--; set_bit1(n,pos); cnt--; for(int i=pos-1;i>=cnt;i--) set_bit1(n,i); for(int i=cnt-1;i>=0;i--) set_bit0(n,i); return n; } void print_bin(int n){ static char* hex2bin[]={ "0000","0001","0010","0011", "0100","0101","0110","0111", "1000","1001","1010","1011", "1100","1101","1110","1111", }; static int mask[]={ 0xf0000000, 0x0f000000, 0x00f00000, 0x000f0000, 0x0000f000, 0x00000f00, 0x000000f0, 0x0000000f, }; for(int i=0;i<8;i++) { printf("%s",hex2bin[(n&mask[i])>>((7-i)*4)]); } printf("\n"); } int main(){ const int N=10; for(int i=0;i<N;i++){ int v=rand()%100+1; int n1=get_nextNP(v); int n2=get_prevNP(v); print_bin(v); print_bin(n1); print_bin(n2); printf("=====================\n"); } }
5.6
交换奇数位与偶数位
Write a program to swap odd and even bits in an integer with as few instructions as possible (e.g., bit 0 and bit 1 are swapped, bit 2 and bit 3 are swapped, etc).
SOLUTION
Mask all odd bits with 10101010 in binary (which is 0xAA), then shift them left to put them in the even bits. Then, perform a similar operation for even bits. This takes a total 5 instructions.
Java 代码如下:
public static int swapOddEvenBits(int x) { return ( ((x & 0xaaaaaaaa) >> 1) | ((x & 0x55555555) << 1) ); }
5.7
找出数组中缺少的数
An array A[1...n] contains all the integers from 0 to n except for one number which is missing. In this problem, we cannot access an entire integer in A with a single operation. The elements of A are represented in binary, and the only operation we can use to access them is “fetch the jth bit of A[i]”, which takes constant time. Write code to find the missing integer. Can you do it in O(n) time?
SOLUTION
Picture a list of binary numbers between 0 to n. What will change when we remove one number? We’ll get an imbalance of 1s and 0s in the least significant bit. That is, before removing the number k, we have this list of least significant bits (in some order):
0 0 0 0 0 1 1 1 1 1 OR 0 0 0 0 0 1 1 1 1
Suppose we secretly removed either a 1 or a 0 from this list. Could we tell which one was removed?
Note that if 0 is removed, we always wind up with count(1) >= count(0). If 1 is removed, we wind up with count(1) < count(0). Therefore, we can look at the least significant bit to figure out in O(N) time whether the missing number has a 0 or a 1 in the least significant bit (LSB). If LSB(missing) == 0, then we can discard all numbers with LSB = 1. If LSB(missing) == 1, we can discard all numbers with LSB = 0.
What about the next iteration, with the second least significant bit (SLSB)? We’ve discarded all the numbers with LSB = 1, so our list looks something like this (if n = 5, and missing = 3):
Our SLSBs now look like 0 0 1 0 1 0. Using the same logic as we applied for LSB, we can figure out that the missing number must have SLSB = 1. Our number must look like xxxx11.
Third iteration, discarding numbers with SLSB = 0:
We can now compute that count(TLSB = 1) = 1 and count(TLSB = 1) = 1. Therefore, TLSB = 0. We can recurse repeatedly, building our number bit by bit:
What is the run-time of this algorithm? On the first pass, we look at O(N) bits. On the second pass, we’ve eliminated N/2 numbers, so we then look at O(N/2) bits. On the third pass, we have eliminated another half of the numbers, so we then look at O(N/4) bits. If we keep going, we get an equation that looks like:
O(N) + O(N/2) + O(N/4) + O(N/8) + ... = O(2N) = O(N)
Our run-time is O(N).
Java代码如下:
public static int findMissing(ArrayList<BitInteger> array) { return findMissing(array, BitInteger.INTEGER_SIZE - 1); } private static int findMissing(ArrayList<BitInteger> input, int column) { if (column < 0) { // Base case and error condition return 0; } ArrayList<BitInteger> oddIndices = new ArrayList<BitInteger>(input.size()/2); ArrayList<BitInteger> evenIndices = new ArrayList<BitInteger>(input.size()/2); for (BitInteger t : input) { if (t.fetch(column) == 0) { evenIndices.add(t); } else { oddIndices.add(t); } } if (oddIndices.size() >= evenIndices.size()) { return (findMissing(evenIndices, column - 1)) << 1 | 0; } else { return (findMissing(oddIndices, column - 1)) << 1 | 1; } }
6.2
残缺棋盘的覆盖
There is an 8x8 chess board in which two diagonally opposite corners have been cut off. You are given 31 dominos, and a single domino can cover exactly two squares. Can you use the 31 dominos to cover the entire board? Prove your answer (by providing an example, or showing why it’s impossible).
SOLUTION
Impossible. Here’s why: The chess board initially has 32 black and 32 white squares. By removing opposite corners (which must be the same color), we’re left with 30 of one color and 32 of the other color. Let’s say, for the sake of argument, that we have 30 black and 32 white squares.
When we lay down each domino, we’re taking up one white and one black square. Therefore, 31 dominos will take up 31 white squares and 31 black squares exactly. On this board, however, we must have 30 black squares and 32 white squares. Hence, it is impossible.
答案是不可能。国际象棋的棋盘原本是32格白色,32格黑色,现将对角线的两块格子切去它们颜色肯定是一样(假设切去的两格是白色)。那么我们现在就有30个白格和32个黑格。根据题意,骨牌恰好能覆盖两个格子。而棋盘上一个骨牌要对应一白格和一个黑格。但是棋盘上白格和黑格的数目不相等,所以肯定不能完成覆盖。
6.5
There is a building of 100 floors. If an egg drops from the Nth floor or above it will break. If it’s dropped from any floor below, it will not break. You’re given 2 eggs. Find N, while minimizing the number of drops for the worst case.
SOLUTION
Observation: Regardless of how we drop Egg1, Egg2 must do a linear search. i.e., if Egg1 breaks between floor 10 and 15, we have to check every floor in between with the Egg2
The Approach:
A First Try: Suppose we drop an egg from the 10th floor, then the 20th, ...
»» If the first egg breaks on the first drop (Floor 10), then we have at most 10 drops total.
»» If the first egg breaks on the last drop (Floor 100), then we have at most 19 drops total (floors 10, 20, ...,90, 100, then 91 through 99).
»» That’s pretty good, but all we’ve considered is the absolute worst case. We should do some “load balancing” to make those two cases more even.
Goal: Create a system for dropping Egg1 so that the most drops required is consistent,
whether Egg1 breaks on the first drop or the last drop.
1. A perfectly load balanced system would be one in which Drops of Egg1 + Drops of Egg2 is always the same, regardless of where Egg1 broke.
2. For that to be the case, since each drop of Egg1 takes one more step, Egg2 is allowed one fewer step.
3. We must, therefore, reduce the number of steps potentially required by Egg2 by one drop each time. For example, if Egg1 is dropped on Floor 20 and then Floor 30, Egg2 is potentially required to take 9 steps. When we drop Egg1 again, we must reduce potential Egg2 steps to only 8. That is, we must drop Egg1 at floor 39.
4. We know, therefore, Egg1 must start at Floor X, then go up by X-1 floors, then X-2, ..., until it gets to 100.
5. Solve for X+(X-1)+(X-2)+...+1 = 100. X(X+1)/2 = 100 -> X = 14 We go to Floor 14, then 27, then 39, ... This takes 14 steps maximum.
有一个100层的高楼。假设有种鸡蛋从第N层和第N层以上掉下来的话,它就会碎;如果从以下的楼层掉的话,就不会碎。现在给你2个这样的鸡蛋,通过丢鸡蛋的方法确定 N的大小,要求丢的次数最少。
解答:
分析:
先不管我们在哪个楼层丢下第一个鸡蛋的,第二个鸡蛋一定是从低的楼层开始逐层丢的来搜索。比如第一个鸡蛋是在第一次10层-没破,第二次在15层-破了,那么第二个鸡蛋会从11层开始一直尝试到14层。
假设我们以10层为间隔来丢第一个鸡蛋,先10层,再20层......
* 如果第一次扔第一个鸡蛋的时候,它就破了。那么总共需要扔10次鸡蛋。
* 如果第一个鸡蛋在第100层扔下时破了,那么总共扔了19次(10,20...90,100层各一次,91到99层的9次。)
* 上述的方法都是在最坏情况下的计算,各种情况下的次数都是不同的。我们现在做一些”负载均衡“,让每种情况下最坏情况下尝试次数都一样。
那我们的目标就是,设计一个方法,让不同情况下第一个鸡蛋和第二个鸡蛋的扔的次数的和为常数。
1. 不管第一个鸡蛋在什么阶段破掉,在最坏情况下第二个鸡蛋扔的次数和第一个鸡蛋扔的次数的和都是相同的。
2. 根据1中的限制,每多扔一次第一个鸡蛋,那么第二个鸡蛋人的次数就要相应的减少1次。
3. 也就是说每次我都需要减少两次扔第一个蛋之间的间距,以满足第2点的要求。
4. 那么假设第一次扔第一个鸡蛋的楼层为X,如果第一次扔第一个鸡蛋摔破的话,第二个鸡蛋尝试的次数就是X-1次,那如果第一个鸡蛋在第二次丢的时候摔破,继续人第二个鸡蛋的尝试次数就只能为X-2次了。也是说第二次扔第一个鸡蛋的楼层应该比第一次到X-1层。依次类推分别为X-2,X-3,...
5. 为了验证所有的楼层,那就要满足下面的式子
X+(X-1)+(X-2)+…+1 >= 100 解得 X>=14
那么我们丢第一个鸡蛋的楼层为14,27,39。。。
6.6
There are one hundred closed lockers in a hallway. A man begins by opening all one hundred lockers. Next, he closes every second locker. Then he goes to every third locker and closes it if it is open or opens it if it is closed (e.g., he toggles every third locker). After his one hundredth pass in the hallway, in which he toggles only locker number one hundred, how many lockers are open?
SOLUTION
Question: For which rounds is a door toggled (open or closed)? A door n is toggled once for each factor of n, including itself and 1. That is, door 15 is toggled on round 1, 3, 5, and 15.
Question: When would a door be left open?
Answer: A door is left open if the number of factors (x) is odd. You can think about this by pairing factors off as an open and a close. If there’s one remaining, the door will be open.
Question: When would x be odd?
Answer: x is odd if n is a perfect square. Here’s why: pair n’s factors by their complements.
For example, if n is 36, the factors are (1, 36), (2, 18), (3, 12), (4, 9), (6, 6). Note that (6, 6) only contributes 1 factor, thus giving n an odd number of factors.
Question: How many perfect squares are there?
Answer: There are 10 perfect squares. You could count them (1, 4, 9, 16, 25, 36, 49, 64, 81, 100), or you could simply realize that you can take the numbers 1 through 10 and square them (1*1, 2*2, 3*3, ..., 10*10). Therefore, there are 10 lockers open.
在一个走廊上有100扇关着的门。有个人开始做下面无聊的事情,他先打开所有的门,然后每隔一扇门的就去看一眼,如果门是关的就把它打开,如果门是开的就把它关上;接着是每隔2扇,接着是每隔3扇...他一共这样做了100次。现在问那些门是开着的?
解答:
在哪几轮某一扇门会被打开或者关掉?假设这扇门是第n扇,只有在n的因数轮第n扇门才会被动。比如第15扇门,只有在第1,15,3,5轮被动到。
哪些门会开着呢?当n的因数个数为奇数的时候,第n扇门是打开。因为一对因数作用下,门刚好是关着的。在奇数情况下,刚好有一个因数多出来,就能使得门是开着的。
在什么情况下n的因数个数是奇数的呢?当n为平方数的时候。通过成对的列出因数,比如36,那列出因数为(1,36),(2,18),(3,12),(4,9),(6,6)。但是(6,6)只能算是一个因数。因此平方数的因数恰好为奇数个。
一共有多少个平方数呢?很简单从1到10做平方运算。
那么一共更有10扇门是开着的,分别是1,4,9,16,25,36,49,64,81,100。
8.2
Imagine a robot sitting on the upper left hand corner of an NxN grid. The robot can only move in two directions: right and down. How many possible paths are there for the robot?
FOLLOW UP
Imagine certain squares are “off limits”, such that the robot can not step on them. Design an algorithm to get all possible paths for the robot.
SOLUTION
Part 1: (For clarity, we will solve this part assuming an X by Y grid)
Each path has (X-1)+(Y-1) steps. Imagine the following paths:
X X Y Y X (move right -> right -> down -> down -> right)
X Y X Y X (move right -> down -> right -> down -> right)
...
Each path can be fully represented by the moves at which we move right. That is, if I were to ask you which path you took, you could simply say “I moved right on step 3 and 4.”
Since you must always move right X-1 times, and you have X-1 + Y-1 total steps, you have to pick X-1 times to move right out of X-1+Y-1 choices. Thus, there are C(X-1, X-1+Y-1) paths (e.g., X-1+Y-1 choose X-1):
(X-1 + Y-1)! / ((X-1)! * (Y-1)!)
Part 2: Code
We can implement a simple recursive algorithm with backtracking:
Java代码如下:
public class Question { public static int[][] maze = new int[10][10]; public static boolean is_free(int x, int y) { if (maze[x][y] == 0) { return false; } else { return true; } } public static ArrayList<Point> current_path = new ArrayList<Point>(); public static boolean getPaths(int x, int y) { Point p = new Point(x, y); current_path.add(p); if (0 == x && 0 == y) { return true; // current_path; } boolean success = false; if (x >= 1 && is_free(x - 1, y)) { // Try right success = getPaths(x - 1, y); // Free! Go right } if (!success && y >= 1 && is_free(x, y - 1)) { // Try down success = getPaths(x, y - 1); // Free! Go down } if (!success) { current_path.remove(p); // Wrong way! Better stop going this way } return success; } public static void main(String[] args) { maze = AssortedMethods.randomMatrix(10, 10, 0, 4); AssortedMethods.printMatrix(maze); getPaths(9, 9); String s = AssortedMethods.listOfPointsToString(current_path); System.out.println(s); } }
8.5
输出符合情况的括号对
Implement an algorithm to print all valid (e.g., properly opened and closed) combinations of n-pairs of parentheses.
EXAMPLE:
input: 3 (e.g., 3 pairs of parentheses)
output: ()()(), ()(()), (())(), ((()))
SOLUTION
We can solve this problem recursively by recursing through the string. On each iteration, we have the index for a particular character in the string. We need to select either a left or a right paren. When can we use left, and when can we use a right paren?
»» Left: As long as we haven’t used up all the left parentheses, we can always insert a left paren.
»» Right: We can insert a right paren as long as it won’t lead to a syntax error. When will we get a syntax error? We will get a syntax error if there are more right parentheses than left.
So, we simply keep track of the number of left and right parentheses allowed. If there are left parens remaining, we’ll insert a left paren and recurse. If there are more right parens remaining than left (eg, if there are more left parens used), then we’ll insert a right paren and recurse.
C++代码如下:
void print_par(char *str,int l,int r,int indx){ if(l<0||r<l) return; if(l==0&&r==0) { str[indx+1]='\0'; printf("%s\n",str); return; } if(l>0){ str[indx]='('; print_par(str,l-1,r,indx+1); } if(l<r){ str[indx]=')'; print_par(str,l,r-1,indx+1); } } int main(){ char s[50]; print_par(s,3,3,0); }
8.7
找零钱问题
Given an infinite number of quarters (25 cents), dimes (10 cents), nickels (5 cents) and pennies (1 cent), write code to calculate the number of ways of representing n cents.
SOLUTION
This is a recursive problem, so let’s figure out how to do makeChange(n) using prior solutions (i.e., sub-problems). Let’s say n = 100, so we want to compute the number of ways of making change of 100 cents. What’s the relationship to its sub-problems?
We know that makeChange(100):
= makeChange(100 using 0 quarters) + makeChange(100 using 1 quarter) + makeChange(100 using 2 quarter) + makeChange(100 using 3 quarter) + makeChange(100 using 4 quarter)
Can we reduce this further? Yes!
= makeChange(100 using 0 quarters) + makeChange(75 using 0 quarter) + makeChange(50 using 0 quarters) + makeChange(25 using 0 quarters) + 1
Now what? We’ve used up all our quarters, so now we can start applying our next biggest denomination: dimes.
This leads to a recursive algorithm that looks like this:
C++代码:
int make_change(int n,int demon){ int next_demon=0; switch(demon){ case 25: next_demon=10; break; case 10: next_demon=5; break; case 5: next_demon=1; break; case 1: return 1; } int way=0; for(int i=0;i*demon<n;i++) way+=make_change(n-i*demon,next_demon); return way; } int main(){ cout<<make_change(70,25)<<endl; }
8.8
八皇后问题
Write an algorithm to print all ways of arranging eight queens on a chess board so that none of them share the same row, column or diagonal.
SOLUTION
We will use a backtracking algorithm. For each row, the column where we want to put the queen is based on checking that it does not violate the required condition.
1. For this, we need to store the column of the queen in each row as soon as we have finalized it. Let ColumnForRow[] be the array which stores the column number for each row.
2. The checks that are required for the three given conditions are:
»» On same Column : ColumnForRow[i] == ColumnForRow[j]
»» On same Diagonal:
(ColumnForRow[i] - ColumnForRow[j] ) == ( i- j) or
(ColumnForRow[j] - ColumnForRow[i]) == (i - j)
Java 代码:
public class Question { static int columnForRow[] = new int [8]; static boolean check(int row) { for (int i = 0; i < row; i++) { int diff = Math.abs(columnForRow[i] - columnForRow[row]); if (diff == 0 || diff == row - i) return false; } return true; } static void printBoard() { System.out.println("-----------------"); for(int i = 0; i < 8; i++){ System.out.print("|"); for(int j = 0; j < 8; j++){ if (columnForRow[i] == j) System.out.print("Q|"); else System.out.print(" |"); } System.out.println("\n-----------------"); } System.out.println(""); } static void PlaceQueen(int row){ if (row == 8) { printBoard(); return; } for (int i = 0; i < 8; i++) { columnForRow[row]=i; if(check(row)){ PlaceQueen(row+1); } } } public static void main(String[] args) { PlaceQueen(0); } }
9.1
合并两个排序数组
You are given two sorted arrays, A and B, and A has a large enough buffer at the end to hold B. Write a method to merge B into A in sorted order.
SOLUTION
This code is a part of the standard merge-sort code. We merge A and B from the back, by comparing each element.
Java代码:
public static void merge(int[] a, int[] b, int n, int m) { int k = m + n - 1; // Index of last location of array b int i = n - 1; // Index of last element in array b int j = m - 1; // Index of last element in array a // Start comparing from the last element and merge a and b while (i >= 0 && j >= 0) { if (a[i] > b[j]) { a[k--] = a[i--]; } else { a[k--] = b[j--]; } } while (j >= 0) { a[k--] = b[j--]; } }
9.3
在旋转数组中查找一个数
Given a sorted array of n integers that has been rotated an unknown number of times, give an O(log n) algorithm that finds an element in the array. You may assume that the array was originally sorted in increasing order.
EXAMPLE:
Input: find 5 in array (15 16 19 20 25 1 3 4 5 7 10 14)
Output: 8 (the index of 5 in the array)
SOLUTION
We can do this with a modification of binary search.
What about duplicates? You may observe that the above function doesn’t give you an efficient result in case of duplicate elements. However, if your array has duplicate entries then we can’t do better than O(n) which is as good as linear search.
For example, if the array is [2,2,2,2,2,2,2,2,3,2,2,2,2,2,2,2,2,2,2], there is no way to find element 3 until you do a linear search.
public static int search(int a[], int l, int u, int x) { while (l <= u) { int m = (l + u) / 2; if (x == a[m]) { return m; } else if (a[l] <= a[m]) { if (x > a[m]) { l = m+1; } else if (x >=a [l]) { u = m-1; } else { l = m+1; } } else if (x < a[m]) u = m-1; else if (x <= a[u]) l = m+1; else u = m - 1; } return -1; }
9.4
If you have a 2 GB file with one string per line, which sorting algorithm would you use to sort the file and why?
SOLUTION
When an interviewer gives a size limit of 2GB, it should tell you something - in this case, it suggests that they don’t want you to bring all the data into memory. So what do we do? We only bring part of the data into memory..
Algorithm:
How much memory do we have available? Let’s assume we have X MB of memory available.
1. Divide the file into K chunks, where X * K = 2 GB. Bring each chunk into memory and sort the lines as usual using any O(n log n) algorithm. Save the lines back to the file.
2. Now bring the next chunk into memory and sort.
3. Once we’re done, merge them one by one.
The above algorithm is also known as external sort. Step 3 is known as N-way merge The rationale behind using external sort is the size of data. Since the data is too huge and we can’t bring it all into memory, we need to go for a disk based sorting algorithm.
9.5
Given a sorted array of strings which is interspersed with empty strings, write a method to find the location of a given string.
Example: find “ball” in [“at”, “”, “”, “”, “ball”, “”, “”, “car”, “”, “”, “dad”, “”, “”] will return 4
Example: find “ballcar” in [“at”, “”, “”, “”, “”, “ball”, “car”, “”, “”, “dad”, “”, “”] will return -1
SOLUTION
Use ordinary binary search, but when you hit an empty string, advance to the next nonempty string; if there is no next non-empty string, search the left half.
Java 代码:
public static int search(String[] strings, String str, int first, int last) { while (first <= last) { // Ensure there is something at the end while (first <= last && strings[last] == "") { --last; } if (last < first) { return -1; // this block was empty, so fail } int mid = (last + first) >> 1; while (strings[mid] == "") { ++mid; // will always find one } int r = strings[mid].compareTo(str); if (r == 0) return mid; if (r < 0) { first = mid + 1; } else { last = mid - 1; } } return -1; } public static int search(String[] strings, String str) { if (strings == null || str == null) { return -1; } if (str == "") { for (int i = 0; i < strings.length; i++) { if (strings[i] == "") { return i; } } return -1; } return search(strings, str, 0, strings.length - 1); }
10.4 Write a method to implement *, - , / operations. You should use only the + operator.
SOLUTION
With an understanding of what each operation (minus, times, divide) does, this problem can be approached logically.
»» Subtraction should be relatively straightforward, as we all know that a - b is the same thing as a + (-1)*b.
»» Multiplication: we have to go back to what we learned in grade school: 21 * 3 = 21 + 21 + 21. It’s slow, but it works.
»» Division is the trickiest, because we usually think of 21 / 3 as something like “if you divide a 21 foot board into 3 pieces, how big is each piece?” If we think about it the other way around, it’s a little easier: “I divided a 21 foot board in x pieces and got pieces of 3 feet each, how many pieces were there?” From here, we can see that if we continuously sub- tract 3 feet from 21 feet, we’ll know how many pieces there are. That is, we continuously subtract b from a and count how many times we can do that.
Java 代码如下:
public class Question { /* Flip a positive sign to negative, or a negative sign to pos */ public static int FnNegate(int a) { int neg = 0; int d = a < 0 ? 1 : -1; while (a != 0) { neg += d; a += d; } return neg; } /* Subtract two numbers by negating b and adding them */ public static int FnMinus(int a, int b) { return a + FnNegate(b); } /* Check if a and b are different signs */ public static boolean DifferentSigns(int a, int b) { return ((a < 0 && b > 0) || (a > 0 && b < 0)) ? true : false; } /* Return absolute value */ public static int abs(int a) { if (a < 0) return FnNegate(a); else return a; } /* Multiply a by b by adding a to itself b times */ public static int FnTimes(int a, int b) { if (a < b) return FnTimes(b, a); // algo is faster if b < a int sum = 0; for (int iter = abs(b); iter > 0; --iter) sum += a; if (b < 0) sum = FnNegate(sum); return sum; } // returns 1, if a/b >= 0.5, and 0 otherwise public static int DefineAndRoundFraction(int a, int b) { if(FnTimes(abs(a), 2) >= abs(b)) return 1; else return 0; } /* Divide a by b by literally counting how many times does b go into * a. That is, count how many times you can subtract b from a until * you hit 0. */ public static int FnDivide(int a, int b) throws java.lang.ArithmeticException { if (b == 0) { throw new java.lang.ArithmeticException("ERROR: Divide by zero."); } int quotient = 0; int divisor = FnNegate(abs(b)); int divend; /* dividend */ for (divend = abs(a); divend >= abs(divisor); divend += divisor) { ++quotient; } if (DifferentSigns(a, b)) quotient = FnNegate(quotient); return quotient; } public static int randomInt(int n) { return (int) (Math.random() * n); } public static void main(String[] args) { for (int i = 0; i < 100; i++) { int a = randomInt(10); int b = randomInt(10); int ans = FnMinus(a, b); if (ans != a - b) { System.out.println("ERROR"); } System.out.println(a + " - " + b + " = " + ans); } for (int i = 0; i < 100; i++) { int a = randomInt(10); int b = randomInt(10); int ans = FnTimes(a, b); if (ans != a * b) { System.out.println("ERROR"); } System.out.println(a + " * " + b + " = " + ans); } for (int i = 0; i < 100; i++) { int a = randomInt(10) + 1; int b = randomInt(10) + 1; System.out.print(a + " / " + b + " = "); int ans = FnDivide(a, b); if (ans != a / b) { System.out.println("ERROR"); } System.out.println(ans); } } }
OBSERVATIONS AND SUGGESTIONS
»» A logical approach of going back to what exactly multiplication and division do comes in handy. Remember that. All (good) interview problems can be approached in a logical, methodical way!
»» The interviewer is looking for this sort of logical work-your-way-through-it approach.
»» This is a great problem to demonstrate your ability to write clean code—specifically, to show your ability to re-use code. For example, if you were writing this solution and didn’t put FnNegate in its own method, you should move it out once you see that you’ll use it multiple times.
»» Be careful about making assumptions while coding. Don’t assume that the numbers are all positive, or that a is bigger than b.
13.1
打印出文件的最后K行
Write a method to print the last K lines of an input file using C++.
SOLUTION
One brute force way could be to count the number of lines (N) and then print from N-10 to Nth line. But, this requires two reads of the file – potentially very costly if the file is large. We need a solution which allows us to read just once and be able to print the last K lines. We can create extra space for K lines and then store each set of K lines in the array. So, initially, our array has lines 0 through 9, then 1 through 10, then 2 through 11, etc (if K = 10). Each time that we read a new line, we purge the oldest line from the array. Instead of shifting the array each time (very inefficient), we will use a circular array. This will allow us to always find
the oldest element in O(1) time.
Example of inserting elements into a circular array:
string L[K]; int lines = 0; while (file.good()) { getline(file, L[lines % K]); // read file line by line ++lines; } // if less than K lines were read, print them all int start, count; if (lines < K) { start = 0; count = lines; } else { start = lines % K; count = K; } for (int i = 0; i < count; ++i) { cout << L[(start + i) % K] << endl; }
OBSERVATIONS AND SUGGESTIONS:
»»
Note, if you do printf(L[(index + i) % K]) when there are %’s in the string, bad things will happen.
13.2
比较Hash表和STL中的Map
Compare and contrast a hash table vs. an STL map. How is a hash table implemented? If the number of inputs is small, what data structure options can be used instead of a hash table?
SOLUTION
Compare and contrast Hash Table vs. STL map
In a hash table, a value is stored by applying hash function on a key. Thus, values are not stored in a hash table in sorted order. Additionally, since hash tables use the key to find the index that will store the value, an insert/lookup can be done in amortised O(1) time (assum- ing only a few collisions in the hashtable). One must also handle potential collisions in a hashtable.
In an STL map, insertion of key/value pair is in sorted order of key. It uses a tree to store values, which is why an O(log N) insert/lookup is required. There is also no need to handle collisions. An STL map works well for things like:
»» find min element
»» find max element
»» print elements in sorted order
»» find the exact element or, if the element is not found, find the next smallest number
How is a hash table implemented?
1. A good hash function is required (e.g.: operation % prime number) to ensure that the hash values are uniformly distributed.
2. A collision resolving method is also needed: chaining (good for dense table entries), probing (good for sparse table entries), etc.
3. Implement methods to dynamically increase or decrease the hash table size on a given criterion. For example, when the [number of elements] by [table size] ratio is greater than the fixed threshold, increase the hash table size by creating a new hash table and transfer the entries from the old table to the new table by computing the index using new hash function.
What can be used instead of a hash table, if the number of inputs is small?
You can use an STL map. Although this takes O(log n) time, since the number of inputs is small, this time is negligible.
19.4
不使用判断语句找出两个数的最大值.
Write a method which finds the maximum of two numbers. You should not use if-else or any other comparison operator.
EXAMPLE
Input: 5, 10
Output: 10
SOLUTION
Let’s try to solve this by “re-wording” the problem. We will re-word the problem until we get something that has removed all if statements.
Rewording 1: If a > b, return a; else, return b.
Rewording 2: If (a - b) is negative, return b; else, return a.
Rewording 3: If (a - b) is negative, let k = 1; else, let k = 0. Return a - k * (a - b).
Rewording 4: Let c = a - b. Let k = the most significant bit of c. Return a - k * c.
We have now reworded the problem into something that fits the requirements. The code for this is below.
int getMax(int a, int b) { int c = a - b; int k = (c >> 31) & 0x1; int max = a - k * c; return max; }
20.3 Write a method to randomly generate a set of m integers from an array of size n. Each element must have equal probability of being chosen.
SOLUTION
Our first instinct on this problem might be to randomly pick elements from the array and put them into our new subset array. But then, what if we pick the same element twice? Ideally, we’d want to somehow “shrink” the array to no longer contain that element. Shrinking is expensive though because of all the shifting required.
Instead of shrinking / shifting, we can swap the element with an element at the beginning of the array and then “remember” that the array now only includes elements j and greater. That is, when we pick subset[0] to be array[k], we replace array[k] with the first element in the array. When we pick subset[1], we consider array[0] to be “dead” and we pick a random element y between 1 and array.size(). We then set subset[1] equal to array[y], and set array[y] equal to array[1]. Elements 0 and 1 are now “dead.” Subset[2] is now chosen from array[2] through array[array.size()], and so on.
Java代码:
public static int[] pickMRandomly(int[] original, int m) { int[] subset = new int[m]; int[] array = original.clone(); for (int j = 0; j < m; j++) { int index = rand(j, array.length - 1); subset[j] = array[index]; array[index] = array[j]; // array[j] is now dead } return subset; }
20.9 Numbers are randomly generated and passed to a method. Write a program to find and maintain the median value as new values are generated.
SOLUTIONS
One solution is to use two priority heaps: a max heap for the values below the median, and a min heap for the values above the median. The median will be largest value of the max heap. When a new value arrives it is placed in the below heap if the value is less than or equal to the median, otherwise it is placed into the above heap. The heap sizes can be equal or the below heap has one extra. This constraint can easily be restored by shifting an element from one heap to the other. The median is available in constant time, so updates are O(lg n).
20.10 Given two words of equal length that are in a dictionary, write a method to transform one word into another word by changing only one letter at a time. The new word you get in each step must be in the dictionary.
EXAMPLE:
Input: DAMP, LIKE
Output: DAMP -> LAMP -> LIMP -> LIME -> LIKE
SOLUTION
Though this problem seems tough, it’s actually a straightforward modification of breadth-first-search. Each word in our “graph” branches to all words in the dictionary that are one edit away. The interesting part is how to implement this—should we build a graph as we go? We could, but there’s an easier way. We can instead use a “backtrack map.” In this backtrack map, if B[v] = w, then you know that you edited v to get w. When we reach our end word, we can use this backtrack map repeatedly to reverse our path. See the code below:
Let n be the length of the start word and m be the number of like sized words in the dictionary. The runtime of this algorithm is O(n*m) since the while loop will dequeue at most m unique words. The for loop is O(n) as it walks down the string applying a fixed number of replacements for each character.
20.13 Given a dictionary of millions of words, give an algorithm to find the largest possible rectangle of letters such that every row forms a word (reading left to right) and every column forms a word (reading top to bottom).
SOLUTION
Many problems involving a dictionary can be solved by doing some preprocessing. Where can we do preprocessing?
Well, if we’re going to create a rectangle of words, we know that each row must be the same length and each column must have the same length. So, let’s group the words of the dictionary based on their sizes. Let’s call this grouping D, where D[i] provides a list of words of length i.
Next, observe that we’re looking for the largest rectangle. What is the absolute largest rectangle that could be formed? It’s (length of largest word) * (length of largest word).
By iterating in this order, we ensure that the first rectangle we find will be the largest.
Now, for the hard part: make_rectangle. Our approach is to rearrange words in list1 into rows and check if the columns are valid words in list2. However, instead of creating, say, a particular 10x20 rectangle, we check if the columns created after inserting the first two words are even valid pre-fixes. A trie becomes handy here.