算法题-经典数学问题
14.Algorithm Gossip: 蒙地卡罗法求 PI
说明
蒙地卡罗为摩洛哥王国之首都,该国位于法国与义大利国境,以赌博闻名。蒙地卡罗的基本原理为以乱数配合面积公式来进行解题,这种以机率来解题的方式带有赌博的意味,虽然在精确度上有所疑虑,但其解题的思考方向却是个值得学习的方式。
解法
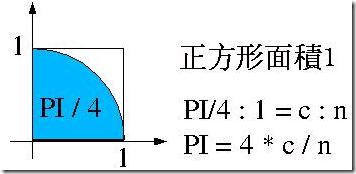
蒙地卡罗的解法适用于与面积有关的题目,例如求PI值或椭圆面积,这边介绍如何求PI值;假设有一个圆半径为1,所以四分之一圆面积就为PI,而包括此四分之一圆的正方形面积就为1,如下图所示:
如果随意的在正方形中投射飞标(点)好了,则这些飞标(点)有些会落于四分之一圆内,假设所投射的飞标(点)有n点,在圆内的飞标(点)有c点,则依比例来算,就会得到上图中最后的公式。
至于如何判断所产生的点落于圆内,很简单,令乱数产生X与Y两个数值,如果X^2+Y^2等于1就是落在圆内。
#include <stdio.h> #include <stdlib.h> #include <time.h> #define N 50000 int main(void) { int i, sum = 0; double x, y; srand(time(NULL)); for(i = 1; i < N; i++) { x = (double) rand() / RAND_MAX; y = (double) rand() / RAND_MAX; if((x * x + y * y) < 1) sum++; } printf("PI = %f\n", (double) 4 * sum / N); return 0; }
15.Algorithm Gossip: Eratosthenes筛选求质数
说明
除了自身之外,无法被其它整数整除的数称之为质数,要求质数很简单,但如何快速的求出质数则一直是程序设计人员与数学家努力的课题,在这边介绍一个着名的 Eratosthenes求质数方法。
解法
首先知道这个问题可以使用回圈来求解,将一个指定的数除以所有小于它的数,若可以整除就不是质数,然而如何减少回圈的检查次数?如何求出小于N的所有质数?
首先假设要检查的数是N好了,则事实上只要检查至N的开根号就可以了,道理很简单,假设A*B = N,如果A大于N的开根号,则事实上在小于A之前的检查就可以先检查到B这个数可以整除N。不过在程序中使用开根号会精确度的问题,所以可以使用 i*i <= N进行检查,且执行更快。
再来假设有一个筛子存放1~N,例如:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 ........ N
先将2的倍数筛去:
2 3 5 7 9 11 13 15 17 19 21 ........ N
再将3的倍数筛去:
2 3 5 7 11 13 17 19 ........ N
再来将5的倍数筛去,再来将7的质数筛去,再来将11的倍数筛去........,如此进行到最后留下的数就都是质数,这就是Eratosthenes筛选方法(Eratosthenes Sieve Method)。
检查的次数还可以再减少,事实上,只要检查6n+1与6n+5就可以了,也就是直接跳过2与3的倍数,使得程序中的if的检查动作可以减少。
实作
#include <stdio.h> #include <stdlib.h> #define N 1000 void create(int*); void filter(int*, int); int main(void) { int primes[N + 1] = {0}; create(primes); int i; for(i = 2; i < N; i++) if(primes[i]) { printf("%4d", i); } return 0; } void create(int* primes) { primes[2] = primes[3] = primes[5] = 1; int i; for(i = 1;6 * i + 5 <= N; i++) { primes[6 * i + 1] = primes[6 * i + 5] = 1; } if(6 * i + 1 <= N) { primes[6 * i + 1] = 1; } int n; for(n = 0;(6 * n + 5) * (6 * n + 5) <= N; n++) { filter(primes, 6 * n + 1); filter(primes, 6 * n + 5); } if((6 * n + 1) * (6 * n + 1) <= N) { filter(primes, 6 * n + 1); } } void filter(int* primes, int i) { if(primes[i]) { int j; for(j = 2; j * i <= N; j++) { primes[j * i] = 0; } } }
16.Algorithm Gossip: 超长整数运算(大数运算)
说明
基于记忆体的有效运用,程序语言中规定了各种不同的资料型态,也因此变数所可以表达的最大整数受到限制,例如123456789123456789这样的 整数就不可能储存在long变数中(例如C/C++等),我们称这为long数,这边翻为超长整数(避免与资料型态的长整数翻译混淆),或俗称大数运算。
解法
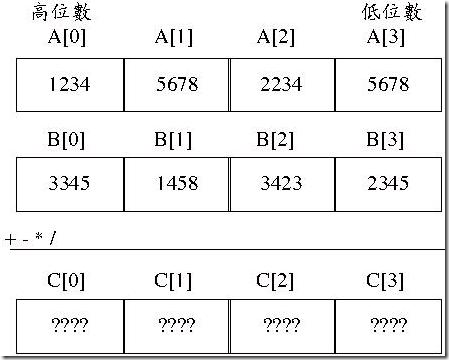
一个变数无法表示超长整数,则就使用多个变数,当然这使用阵列最为方便,假设程序语言的最大资料型态可以储存至65535的数好了,为了计算方便及符合使用十进位制的习惯,让每一个阵列元素可以储存四个位数,也就是0到9999的数,例如:
很多人问到如何计算像50!这样的问题,解法就是使用程序中的乘法函式,至于要算到多大,就看需求了。
由于使用阵列来储存数值,关于数值在运算时的加减乘除等各种运算、位数的进位或借位就必须自行定义,加、减、乘都是由低位数开始运算,而除法则是由高位数开始运算,这边直接提供加减乘除运算的函式供作参考,以下的N为阵列长度。
#include <stdio.h> #include <stdlib.h> #define N 1000 int main(void) { int i, j; int prime[N+1]; for(i = 2; i <= N; i++) prime[i] = 1; for(i = 2; i*i <= N; i++) { // 这边可以改进 if(prime[i] == 1) { for(j = 2*i; j <= N; j++) { if(j % i == 0) prime[j] = 0; } } } for(i = 2; i < N; i++) { if(prime[i] == 1) { printf("%4d ", i); if(i % 16 == 0) printf("\n"); } } printf("\n"); return 0; } void add(int *a, int *b, int *c) { int i, carry = 0; for(i = N - 1; i >= 0; i--) { c[i] = a[i] + b[i] + carry; if(c[i] < 10000) carry = 0; else { // 进位 c[i] = c[i] - 10000; carry = 1; } } } void sub(int *a, int *b, int *c) { int i, borrow = 0; for(i = N - 1; i >= 0; i--) { c[i] = a[i] - b[i] - borrow; if(c[i] >= 0) borrow = 0; else { // 借位 c[i] = c[i] + 10000; borrow = 1; } } } void mul(int *a, int b, int *c) { // b 为乘数 int i, tmp, carry = 0; for(i = N - 1; i >=0; i--) { tmp = a[i] * b + carry; c[i] = tmp % 10000; carry = tmp / 10000; } } void div(int *a, int b, int *c) { // b 为除数 int i, tmp, remain = 0; for(i = 0; i < N; i++) { tmp = a[i] + remain; c[i] = tmp / b; remain = (tmp % b) * 10000; } }
18.Algorithm Gossip: 最大公因数、最小公倍数、因式分解
说明
最大公因数使用辗转相除法来求,最小公倍数则由这个公式来求:
GCD * LCM = 两数乘积
解法
最大公因数可以使用递回与非递回求解,因式分解基本上就是使用小于输入数的数值当作除数,去除以输入数值,如果可以整除就视为因数,要比较快的解法就是求出小于该数的所有质数,并试试看是不是可以整除,求质数的问题是另一个课题,请参考 Eratosthenes 筛选求质数。
实作(最大公因数、最小公倍数)
#include <stdio.h> #include <stdlib.h> int main(void) { int m, n, r; int s; printf("輸入兩數:"); scanf("%d %d", &m, &n); s = m * n; while(n != 0) { r = m % n; m = n; n = r; } printf("GCD:%d\n", m); printf("LCM:%d\n", s/m); return 0; }
实作(因式分解)
C(不用质数表)
#include <stdio.h> #include <stdlib.h> int main(void) { int i, n; printf("請輸入整數:"); scanf("%d", &n); printf("%d = ", n); for(i = 2; i * i <= n;) { if(n % i == 0) { printf("%d * ", i); n /= i; } else i++; } printf("%d\n", n); return 0; }
C(使用质数表)
#include <stdio.h> #include <stdlib.h> #define N 1000 int prime(int*); // 求質數表 void factor(int*, int); // 求factor int main(void) { int ptable[N+1] = {0}; int count, i, temp; count = prime(ptable); printf("請輸入一數:"); scanf("%d", &temp); factor(ptable, temp); printf("\n"); return 0; } int prime(int* pNum) { int i, j; int prime[N+1]; for(i = 2; i <= N; i++) prime[i] = 1; for(i = 2; i*i <= N; i++) { if(prime[i] == 1) { for(j = 2*i; j <= N; j++) { if(j % i == 0) prime[j] = 0; } } } for(i = 2, j = 0; i < N; i++) { if(prime[i] == 1) pNum[j++] = i; } return j; } void factor(int* table, int num) { int i; for(i = 0; table[i] * table[i] <= num;) { if(num % table[i] == 0) { printf("%d * ", table[i]); num /= table[i]; } else i++; } printf("%d\n", num); }
19.Algorithm Gossip: 完美数
说明
如果有一数n,其真因数(Proper factor)的总和等于n,则称之为完美数(Perfect Number),例如以下几个数都是完美数:
6 = 1 + 2 + 3
28 = 1 + 2 + 4 + 7 + 14
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
程序基本上不难,第一眼看到时会想到使用回圈求出所有真因数,再进一步求因数和,不过若n值很大,则此法会花费许多时间在回圈测试上,十分没有效率,例如求小于10000的所有完美数。
解法
如何求小于10000的所有完美数?并将程序写的有效率?基本上有三个步骤:
求出一定数目的质数表
利用质数表求指定数的因式分解
利用因式分解求所有真因数和,并检查是否为完美数
步骤一 与 步骤二 在之前讨论过了,问题在步骤三,如何求真因数和?方法很简单,要先知道将所有真因数和加上该数本身,会等于该数的两倍,例如:
2 * 28 = 1 + 2 + 4 + 7 + 14 + 28
等式后面可以化为:
2 * 28 = (20 + 21 + 22) * (70 + 71)
所以只要求出因式分解,就可以利用回圈求得等式后面的值,将该值除以2就是真因数和了;等式后面第一眼看时可能想到使用等比级数公式来解,不过会使用到次方运算,可以在回圈走访因式分解阵列时,同时计算出等式后面的值,这在下面的实作中可以看到。
#include <stdio.h> #include <stdlib.h> #define P 10000 #define N 5000 void create(int*); // 建立質數表 void filter(int*, int); void factor(int, int*, int*); // 因數分解 int isPerfect(int, int*); // 判斷完美數 int main(void) { int primes[N + 1] = {0}; create(primes); int i; for(i = 2; i <= P; i++) if(isPerfect(i, primes)) { printf("Perfect Number%5d\n", i); } return 0; } void create(int* primes) { primes[2] = primes[3] = primes[5] = 1; int i; for(i = 1;6 * i + 5 <= N; i++) { primes[6 * i + 1] = primes[6 * i + 5] = 1; } if(6 * i + 1 <= N) { primes[6 * i + 1] = 1; } int n; for(n = 0;(6 * n + 5) * (6 * n + 5) <= N; n++) { filter(primes, 6 * n + 1); filter(primes, 6 * n + 5); } if((6 * n + 1) * (6 * n + 1) <= N) { filter(primes, 6 * n + 1); } } void filter(int* primes, int i) { if(primes[i]) { int j; for(j = 2; j * i <= N; j++) { primes[j * i] = 0; } } } void factor(int num, int* factors, int* primes) { int i, j; for(i = 2, j = 0; i * i <= num;) if(primes[i] && num % i == 0) { factors[j++] = i; num /= i; } else { i++; } factors[j] = num; } int isPerfect(int num, int* primes) { int factors[N / 2 + 1] = {0}; factor(num, factors, primes); int s = 1; int i = 0; while(factors[i] != 0) { int r = 1; int q = 1; do { r *= factors[i]; q += r; i++; } while(factors[i - 1] == factors[i]); s *= q; } return s / 2 == num; }
22.Algorithm Gossip: 中序式转后序式(前序式)
说明
平常所使用的运算式,主要是将运算元放在运算子的两旁,例如a+b/d这样的式子,这称之为中序(Infix)表示式,对于人类来说,这样的式子很容易理 解,但由于电脑执行指令时是有顺序的,遇到中序表示式时,无法直接进行运算,而必须进一步判断运算的先后顺序,所以必须将中序表示式转换为另一种表示方 法。
可以将中序表示式转换为后序(Postfix)表示式,后序表示式又称之为逆向波兰表示式(Reverse polish notation),它是由波兰的数学家卢卡谢维奇提出,例如(a+b)*(c+d)这个式子,表示为后序表示式时是ab+cd+*。
解法
用手算的方式来计算后序式相当的简单,将运算子两旁的运算元依先后顺序全括号起来,然后将所有的右括号取代为左边最接近的运算子(从最内层括号开始),最后去掉所有的左括号就可以完成后序表示式,例如:
a+b*d+c/d => ((a+(b*d))+(c/d)) -> bd*+cd/+
如果要用程序来进行中序转后序,则必须使用堆叠,算法很简单,直接叙述的话就是使用回圈,取出中序式的字符,遇运算元直接输出,堆叠运算子与左括号, ISP>ICP的话直接输出堆叠中的运算子,遇右括号输出堆叠中的运算子至左括号。
例如(a+b)*(c+d)这个式子,依算法的输出过程如下:
|
OP |
STACK |
OUTPUT |
|
( |
( |
- |
|
a |
( |
a |
|
+ |
(+ |
a |
|
b |
(+ |
ab |
|
) |
- |
ab+ |
|
* |
* |
ab+ |
|
( |
*( |
ab+ |
|
c |
*( |
ab+c |
|
+ |
*(+ |
ab+c |
|
d |
*(+ |
ab+cd |
|
) |
* |
ab+cd+ |
|
- |
- |
ab+cd+* |
如果要将中序式转为前序式,则在读取中序式时是由后往前读取,而左右括号的处理方式相反,其余不变,但输出之前必须先置入堆叠,待转换完成后再将堆叠中的 值由上往下读出,如此就是前序表示式。
实作
#include <stdio.h> #include <stdlib.h> int postfix(char*); // 中序转后序 int priority(char); // 决定运算子优先顺序 int main(void) { char input[80]; printf("输入中序运算式:"); scanf("%s", input); postfix(input); return 0; } int postfix(char* infix) { int i = 0, top = 0; char stack[80] = {'\0'}; char op; while(1) { op = infix[i]; switch(op) { case '\0': while(top > 0) { printf("%c", stack[top]); top--; } printf("\n"); return 0; // 运算子堆叠 case '(': if(top < (sizeof(stack) / sizeof(char))) { top++; stack[top] = op; } break; case '+': case '-': case '*': case '/': while(priority(stack[top]) >= priority(op)) { printf("%c", stack[top]); top--; } // 存入堆叠 if(top < (sizeof(stack) / sizeof(char))) { top++; stack[top] = op; } break; // 遇 ) 输出至 ( case ')': while(stack[top] != '(') { printf("%c", stack[top]); top--; } top--; // 不输出( break; // 运算元直接输出 default: printf("%c", op); break; } i++; } } int priority(char op) { int p; switch(op) { case '+': case '-': p = 1; break; case '*': case '/': p = 2; break; default: p = 0; break; } return p; }