奇异广告面试
应聘算法工程师
一面:
1. 两个球分别沿不同轨道往下走,哪个先到?轨道如下:
可以画出他们的v-t图像分析,左边的先到。
2. 二叉搜索树,寻找大于等于a的那个元素?(a有可能不在树里面,寻找后继)
寻找后继:
如果节点x的右子树非空,那么其右子树的最左节点即是;
如果节点x的右子树为空,且x有后继,那么其后继是它的最低祖先y,并且要满足y的左儿子也是x的祖先。
二面:
1. 写快排。时间复杂度?分析空间复杂度?partition的时候先递归短的一边,是否可以优化空间负责度?(这个可以画出递归的树状结构来分析)
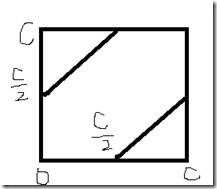
2. 一个圆上,随机选两个点,他们的连线通过圆心的概率?
概率是0,可以用测度去证明:
两个点的取值范围是[0,C],C是圆的周长。所有的取值可能组合是正方形区域,满足条件的只有两条线段。所以概率为0。
3. 2个筛子,扔的话出现的点数之和是2。。。。12,概率是不同的。如何设计这两个筛子,让点数之和出现1。。。。12的概率相同?(第2个筛子三面是0,另外3面是6)。
三面:
1. 虚函数实现机制?虚表。(每个带有虚函数的类有一个虚函数表;它的每个对象有一个虚函数指针,指向该类的虚函数表。)
2. 如何写check函数,这个是他们工程中的一个实际问题。(我的答案是定义一个局部对象,在析构函数里面abort)。
3. 写shuffle函数(实现对数组的重排,要求元素出现在各个位置等概率)
代码:
void shuffle(int *a, int n)
{
if(NULL == a || n < 1) return;
for(int i=n-1;i>=0;i--)
{
int tmp = rand()%i;
swap(a[i],a[tmp]);
}
}
证明:
第一次选一个元素,概率为1/n;
后面的类似。