Hadamard 变换中的归一化问题
2011-9-6 10:16:12
find_sad_16x16是一个比较重要的函数, 下面是其被调用过程:

在find_sad_16x16中有一个/4和/2的问题, 这其实就牵扯到hadamard变换的问题.
在H.264乐园论坛上给出的解释如下:
hadamard 变换本身就有一个 /2 的操作,因此每次变换都要对所有系数进行 /2。而 find_sad_16x16 函数执行了两次 hadamard 变换:首先对 256 个系数进行一次,其次对所有 DC 系数再做一次,因此对DC 系数应该 /4,而对 AC 系数应该 /2。find_sad_16x16 函数中的:M4[ i ][j]=M0[0][ i ][0][j]/4;就是对DC 系数 /4,而最后的:best_intra_sad2 = best_intra_sad2/2;可以认为是对 AC 系数的变相 /2。但这里相当于是对所有系数 /2,所以 DC 系数多了一次 /2。这个多的一次就不知道原因了。
下面是给出的一个比较理论的解释:
4阶hadamard变换的定义式本身就是包含了这个/2的。可以见http://en.wikipedia.org/wiki/Hadamard_transform , 这里再多解释一点
假设hadamard变换没有/2, 变换矩阵为:

这时对一个列向量v = (1, 1, 1, 1)'做变换,即用变换矩阵左乘列向量v,得到的变换后向量v' = (4, 0, 0,0)'。
现在观察v和v',在欧氏空间中,对一个向量的"大小"的衡量就是其长度,通过计算内积得到。那么
len(v) = sqrt( 1^2 + 1^2 + 1^2 + 1^2) = 2
len(v') = sqrt( 4^2 + 0^2 + 0^2 + 0^2) = 4
由此可见如果没有那个/2,变换前后,该向量的长度发生了变化。这样的变换是违背正交变换的定义的。
所以,作为正交变换的hadamard变换,必须要有这个/2的归一化。
对于DCT变换(非整数)也是归一化的, 整数变换也是正交变换,所以也一定会满足归一化的。
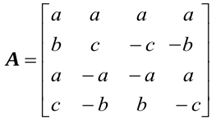
注意计算的时候必须把scaling matrix考虑进来, 下面的变换公式还没有分离出scaling matrix
取a=1/2, 可以同上进行验证.
下面参考一篇论文对h.264中的整数DCT变换再复习一下:
<<!H.264的整数DCT变换编码与量化过程>>
- 采用整数DCT变换的原因:
H.264中 的 变 换 编 码 和 以 前 各 种 标 准 中 的DCT有 所 不同, 以 前 标 准 中 直 接 采 用DCT的 定 义 进 行 变 换, 会 带 来 两个问题: 第一, 需要进行浮点数操作,从而造成系统设计及运算上的复杂性; 第二, 由于变换核都是无理数, 而有限精度的浮点数不可能精确地表示无理数, 再加上浮点数的运算可能会引入舍入误差, 这就使得在具体实现时会导致编解码的不匹配, 即反变换的输出结果和正变换的输入不一致. 为了克服这些问题, H.264采用基于 4x4 块的整数操作而不是实数运算, 使得变换操作仅用整数加减和移位操作就可以完成, 这样既降低了设计复杂度, 又避免了编解 码 误 匹 配 等 问 题, 能 够 得 到 与4x4 DCT变 化 类 似 的 编 码效果, 由此带来的编码性能的减少微乎其微.
- 具体的变换公式


- 具体处理过程

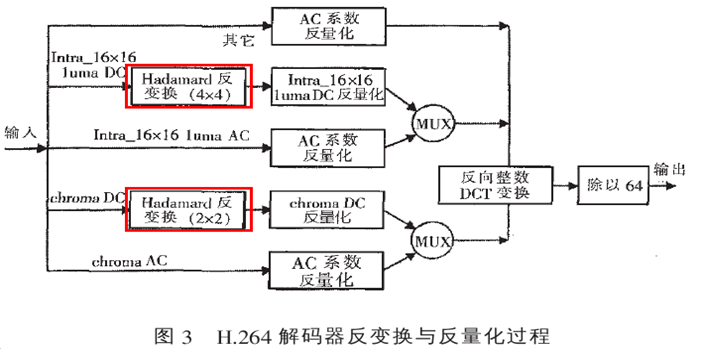
这儿有一个值得注意的问题, 之前也提过, 就是 Dc系数是先进行的反Hadamard变换, 然后才进行的反量化,
具体原因在书《H.264 And MPEG-4 Video Compression Video Coding For Next-Generation Multimedia》的第 6.4.9 小节有提到, 如下:

对应中文翻译如下:

xkfz007
2011年9月6日 13:22:45



