读书笔记之:程序员面试宝典-1
第2部分 C/C++程序设计
1. 二进制位变换
对于整型x:
x&(x-1)的结果是x最右边的1被置为0
这儿有详细介绍:http://www.cnblogs.com/xkfz007/archive/2012/06/27/2566478.html
2. 类型转换
这儿提到的类型转换主要是指,浮点型和整型之间的转换。
例如:
float x=2.5f;
则printf("%#x\n",*(int*)&x);//0x40200000
printf("%#x\n",(int&)x);//0x40200000(这个需要在C++下编译)
(int&)x效果等价于*(int*)&x,这是C++中可以编译通过(VC,g++都可以),在C中是不可以的。
下面一段程序:
int main(){
unsigned int a=0x77777777;
unsigned char i=(unsigned char)a;
char *b=(char*)&a;
char c=*(char*)&a;
printf("%#08x,%#08x,%#08x",i,*b,c);
return 0;
}
输出为:0x000077,0x000077,0x000077
若a=0x7ffffff7;
输出为:0x0000f7,0xfffffff7,0xfffffff7
若a=0x7fffff77;
输出为:0x000077,0x000077,0x000077
若a=0xffffff77;
输出为:0x000077,0x000077,0x000077
若a=0xfffffff7
输出为:0x0000f7,0xfffffff7,0xfffffff7
所以可以得出结论:i和*b和c其实都是一个字节,只是如果值为负的时候要在前面补1
3.运算符符问题
看下面代码的输出:
using namespace std;
int main(){
unsigned char a=0xA5;
unsigned char b=~a>>4+1;
printf("b=%d\n",b);
return 0;
}
这儿需要注意的是~的优先级高于+,+的优先级高于>>,所以先取反,然后求和最后移位。
正常情况下,对10100101取反得01011010,然后右移5位得到00000010,为2,但是运行后结果是0xfa(250)
解释如下:

4. x&(x-1)又一个应用实例

在分析该表达式的实现思路之前,首先说明该表达式的作用就是求两数的平均值。也就是说,像上面当 x为 729,y为271时函数的返回值是500 。下面说明该表达式的思路。
我们先了解下面几种情况:
1. 当两个数所有为 1 和为 0 的位都相同时,这两个数的平均值就是 (x & y) 。比如当 x 和 y 都等于 1100 时,x & y 的值也是 1100 ,我们也可以说此时求 x 和 y 的平均数可以用 (x & y) 来求得。
2. 当两个数中的所有对应位有且只有一个为 1 时,那么这两个数的平均值由 (x^y)>>1 表达式求得。比如当 x 为 101100 (十进制 44),y 为 010010 (十进制 18) 时,x ^ y 的值为 111110 ,然后再将 111110 向右移动 1 位后得 11111 (十进制为 31),也就是 (44 + 18)/2 = 31 。
由上面的 情况1 和 情况2 我们知道,将它们两者结合起来便可求得随意两个整数的平均值。下面以 x 等于 12, y 等于 24 为例说明:
x 的二进制数位 1100 ,y 的二进制数为 11000 。我们先将 x 和 y 做相与运算:
01100
11000 &
--------------
01000
实际上,像上面的运算,我们也可以直接看成是 情况1 中的运算,即相当于执行:01000 & 01000 ,最后值仍然是 01000 。
好,经过上面的与运算后,看起来是将 01100 和 11000 分别去掉了 01000 这部分,所以剩下来的就是 00100 和 10000 。当我们执行 x^y 时:
01100
11000 ^
-----------
10100
由上可见,异或的运算正好也是去掉了 01000 ,然后将剩下来的 00100 和 10000 这两部分进行相加,所以求这两部分的平均数只要向右移动 1 位即可。
综 上可得,我们求平均数的过程是先用与运算对数值做部分的提取,然后用异或并右移运算获得余下部分的平均值,因此这两部分的平均值相加后就得出了原来两数的 平均值。实际上,这是一个加法分解然后综合的过程。如上面的 12 和 24,先做与运算,也就相当于从 12 和 24 里分别先减去 4,剩下 8 和 16,再将这两数相加得 24 (异或运算),然后再除以2(右移),结果为 12 。最后 12 + 4 等于 16 即得最后所要的结果。
尽管上面的过程看来上去实际用处不是很大,但如果是用在没有乘除法指令的简单单片机系统,移位和逻辑运算操作就显得很重要了。
5. 比较两个数
不使用判断语句得到两个数中较大的一个:
方案一:
int max=(a+b+abs(a-b))/2;
方案二:
int flag=(((a - b) >> (8 * sizeof(int) - 1))) & 0x01; //获得两者差的符号位
int buf[2]={a,b};
int max=buf[flag];//如果flag=0,说明a>b,否则a<b
或者:
int max=(flag * b) + ((1 - flag) * a);
参考:http://blog.csdn.net/mougaidong/article/details/6904099
测试代码如下:
int x,y;
int z;
int i;
double m;
srand((int)time(NULL));
for(i=0;i<10;i++)
{
x=rand()%100;
y=rand()%100;
m=(x+y)/2.0;
z=(x&y)+((x^y)>>1);
printf("%4d%4d%5.1f%4d%4d%4d\n",x,y,m,x&y,x^y,z);
}
}
int test2(){
int i;
srand((int)time(NULL));
for(i=0;i<10;i++){
int x=rand()%100;
int y=rand()%100;
int buf[2]={x,y};
unsigned int z;
z=x-y;
z>>=31;
printf("%3d%3d%3d\n",x,y,buf[z]);
}
return 0;
}
输出如下(左边是test1函数,右边是test2函数):
6. 删除C/C++程序中的注释
7. const用法,在C与C++中的不同

在const成员函数中,使用mutable修饰成员变量后,就可以修改类成员变量了。
8. 内存对齐
不同编译器的内存对齐情况

下面的代码:
int a;
char b;
int c;
char *p=(char*)&a;
printf("%#08x\n",&a);
printf("%#08x\n",&b);
printf("%#08x\n",&c);
printf("%#08x\n",p);
printf("%#08x\n",p+1);
printf("%#08x\n",p+2);
printf("%#08x\n",p+3);
return 0;
}
gcc编译运行如下:
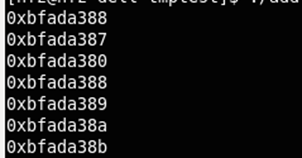

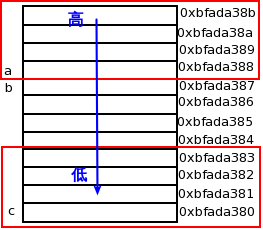
最右边的图表示的是内存中的排列方式
这儿要注意内存的增长方向:高->低
http://www.cnblogs.com/xkfz007/archive/2012/06/22/2558935.html
数组在内存中的存储:
下面是一段测试代码:
int i=-1,a[]={1,2,3,4,5};
char *p=NULL;
printf("%#08x\n",&i);
printf("%#08x\n",a);
printf("%#08x\n",&p);
for(i=0;i<5;i++){
printf("%d: ",i);
p=(char*)&a[i];
printf("%#08x ",p);
printf("%#08x ",p+1);
printf("%#08x ",p+2);
printf("%#08x\n",p+3);
}
}
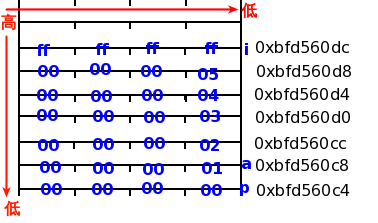
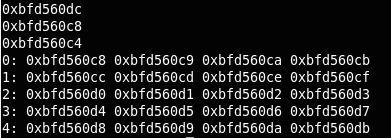
9. C++中类也遵循内存对齐
注意:类中的方法不占用空间。类中的静态变量是分配在全局数据区的,而sizeof计算的是栈中分配的大小。
参 数为结构或类。Sizeof应用在类和结构的处理情况是相同的。但有两点需要注意,第一、结构或者类中的静态成员不对结构或者类的大小产生影响,因为静态 变量的存储位置与结构或者类的实例地址无关。第二、没有成员变量的结构或类的大小为1,因为必须保证结构或类的每一个实例在内存中都有唯一的地址。
10. sizeof空类,多重继承
一个空类所占的空间为1,多重继承的空类所占空间还是1,但是虚继承设计虚表(虚指针),所以至少有一个指针的大小
11. 指针减法运算
#include <stdlib.h>
int main(int argc, char *argv[])
{
int arr[5] = {1,2,3,4,5};
int *ptr = arr;
printf("%d\n",ptr[4]-ptr[0]);
return 0;
}
运行输出:4
更换为字符数组,测试结果一样。
《C 和指针》P110 分析如下:两个指针相减的结果的类型为ptrdiff_t,它是一种有符号整数类型。减法运算的值为两个指针在内存中的距离(以数组元素的长度为单位,而 非字节),因为减法运算的结果将除以数组元素类型的长度。所以该结果与数组中存储的元素的类型无关。
ptrdiff_t是signed类型,用于存放同一数组中两个指针之间的差距,它可以使负数,std::ptrdiff_t.
size_type是unsigned类型,表示容器中元素长度或者下标,vector<int>::size_type i = 0;
difference_type是signed类型,表示迭代器差距,vector<int>:: difference_type = iter1-iter2.
前二者位于标准类库std内,后二者专为STL对象所拥有。
12. 获取成员变量偏移量的两种方式
第一种方式是MFC里使用广泛的宏:#define OFFSET(structure, member) ((int)&((structure*)0)->member); 正如我们平时通过某对象的地址指针访问某个成员变量一样,这里只是强制使用0作为该地址,但区别是并没有通过该地址去访问成员变量,而只是用&操 作符来获取该成员变量的地址,所以不会出现访问违规的情况。所以,完全可以用此类声明一个对象,然后用该对象某成员变量地址减去该对象首地址获取偏移量, 只是纯虚类无法这样实现。
另一种方式是通过域操作符取成员变量的地址。例如一个类Test有int 型成员变量x,则可以通过int Test::* pOffset = &Test::x 获得该偏移量,然后通过int nOffset = reinterpret_cast<int>(*(void**)(&pOffset))将其转化为整型量。
另外,以上这两种方式都对静态成员无效。
下面给出了获取成员变量地址的方式:
public:
A():m_a(1),m_b(2){
cout<<"A()"<<endl;
}
~A(){
cout<<"~A()"<<endl;
}
void fun(){
cout<<"A:fun "<<m_a<<" "<<m_b<<" "<<endl;
}
public:
int m_a;
int m_b;
static int s_a;
};
int A::s_a=3;
class B{
public:
B():m_c(3){
cout<<"B()"<<endl;
}
~B(){
cout<<"~B()"<<endl;
}
void fun(){
cout<<"B:fun "<<m_c<<endl;
}
public:
int m_c;
};
void test1(){
A a;
B *p=(B*)(&a);
cout<<"&a:"<<&a<<endl;
cout<<"&(a.m_a):"<<&(a.m_a)<<endl;
cout<<"&(a::s_a)"<<&a.s_a<<endl;
cout<<"&(A::s_a)"<<&A::s_a<<endl;
int A::* q=&A::m_a;
cout<<"&A::m_a:"<<reinterpret_cast<int>(*(void**)(&q))<<endl;
q=&A::m_b;
cout<<"&A::m_b:"<<reinterpret_cast<int>(*(void**)(&q))<<endl;
int B::* t=&B::m_c;
cout<<"&B::m_c:"<<reinterpret_cast<int>(*(void**)(&t))<<endl;
p->fun();
}
输出如下:

13. 指针与句柄

第8章 递归问题
14. 输入两个字符串,比如abdbcc和abc,输出第二个字符串在第一个字符串中的连接次序,即输出125,146,145,146.

递归代码如下:
 View Code
View Code
#include <cstdio>
#include <cstring>
using namespace std;
void PrintArray(char *p_str,char*s_str,
int *print_arr,int p_len,
int s_len,int print_arr_num,
int p_start_num,int s_start_num){
int pStartnum=p_start_num,
sStartnum=s_start_num;
int printNum=print_arr_num;
if(printNum==s_len){
for(int i=0;i<s_len;i++)
cout<<*(print_arr+i)<<' ';
cout<<endl;
return;
}
for(int i=pStartnum;i<p_len;i++){
for(int j=sStartnum;j<s_len;j++){
if(*(p_str+i)==*(s_str+j)) {
print_arr[printNum]=i+1;
pStartnum=i;
sStartnum=j;
PrintArray(p_str,s_str,
print_arr,p_len,s_len,
printNum+1,pStartnum+1,
sStartnum+1);
}
}
}
}
void ConnectSequence(char* p_str,char *s_str){
if(NULL==p_str&&NULL==s_str){
cout<<"string error"<<endl;
return ;
}
int p_len=strlen(p_str);
int s_len=strlen(s_str);
int *print_arr=new int[s_len];
unsigned int print_arr_num=0;
if(NULL==print_arr){
cout<<"allocate error"<<endl;
return ;
}
PrintArray(p_str,s_str,print_arr,p_len,s_len,0,0,0);
}
int main(){
char parStr[]="abdbcca";
char sonStr[]="abc";
ConnectSequence(parStr,sonStr);
return 0;
}
输出:

非递归代码如下:
15. 给出如下递归表达式的非递归计算方法:

递归和非递归的代码如下:
 View Code
View Code
#include <cstdlib>
using namespace std;
long long f(int m,int n){
if(1==m)
return n;
else if(1==n)
return m;
else
return f(m-1,n)+f(m,n-1);
}
long long f2(int m,int n){
const int M=m;
const int N=n;
long long a[M][N];
for(int i=0;i<M;i++)
a[i][0]=i+1;
for(int j=1;j<N;j++)
a[0][j]=j+1;
for(int i=1;i<M;i++)
for(int j=1;j<N;j++)
a[i][j]=a[i-1][j]+a[i][j-1];
return a[M-1][N-1];
}
int main(){
for(int i=0;i<10;i++){
int m=rand()%8;
int n=rand()%8;
long long y=f(m,n);
long long y2=f2(m,n);
cout<<'<'<<m<<','<<n<<"> "<<y<<' '<<y2<<endl;
}
}
16. zig-zag扫描问题

实现代码如下:
 View Code
View Code
#include <iomanip>
using namespace std;
void zigzag(int n){
const int N=n;
int a[N][N];
int squa=N*N;
int b[N*N][2];
for(int i=0;i<N;i++)
for(int j=0;j<N;j++){
int s=i+j;
if(s<N) {
a[i][j]=s*(s+1)/2+((i+j)%2==0?j:i);
}
else{
s=(N-1-i)+(N-1-j);
a[i][j]=squa-s*(s+1)/2-(N-((i+j)%2==0?j:i));
}
b[a[i][j]][0]=i;
b[a[i][j]][1]=j;
}
for(int i=0;i<N;i++){
for(int j=0;j<N;j++)
cout<<setw(2)<<a[i][j]<<" ";
cout<<endl;
}
for(int i=0;i<N*N;i++) {
for(int j=0;j<2;j++)
cout<<setw(2)<<b[i][j]<<' ';
cout<<endl;
}
}
int main(){
int n=4;
zigzag(n);
}
17. 两个数组匹配的问题:
A,B两个数组是等长度,但顺序不同,对两个数组中的数进行匹配。

常规解法的代码如下:
 View Code
View Code
using namespace std;
void match(int a[],int b[],int k){
for(int i=0;i<k;i++){
for(int j=0;j<k;j++){
if(a[i]==b[j]){
cout<<"a["<<i<<"] match b["<<j<<"]"<<endl;
break;
}
}
}
}
int main(){
int a[10]={1,2,3,4,5,6,7,8,9,10};
int b[10]={10,6,4,5,1,8,7,9,3,2};
int k=sizeof(a)/sizeof(int);
match(a,b,k);
return 0;
}
输出如下:
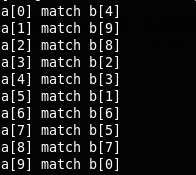
一种更好的方法:
18. 螺旋队列问题


具体程序如下:
 View Code
View Code
#include <iomanip>
#define max(a,b) ((a)>(b)?(a):(b))
#define abs(a) ((a)>0?(a):-(a))
using namespace std;
int spiral(int x,int y){
int t=max(abs(x),abs(y));
int u=t+t;
int v=u-1;
v=v*v+u;
if(x==-t)
v+=u+t-y;
else if(y==-t)
v+=3*u+x-t;
else if(y==t)
v+=t-x;
else
v+=y-t;
return v;
}
int main(){
for(int i=-4;i<=4;i++){
for(int j=-4;j<=4;j++)
cout<<setw(3)<<spiral(j,i)<<' ';
cout<<endl;
}
}
程序输出如下:
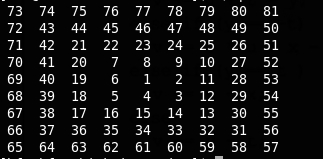
扩展问题

代码如下:
 View Code
View Code
#include <iomanip>
#define max(a,b) ((a)>(b)?(a):(b))
#define abs(a) ((a)>0?(a):-(a))
using namespace std;
int spiral(int x,int y){
int t=max(abs(x),abs(y));
int u=t+t;
int v=u-1;
v=v*v+u;
if(x==-t)
v+=u+t-y;
else if(y==-t)
v+=3*u+x-t;
else if(y==t)
v+=t-x;
else
v+=y-t;
return v;
}
void test1(){
for(int i=-4;i<=4;i++){
for(int j=-4;j<=4;j++)
cout<<setw(3)<<spiral(j,i)<<' ';
cout<<endl;
}
}
int a[10][10];
void spiral2(int n){
int m=1;
for(int i=0;i<n/2;i++){
for(int j=0;j<n-i;j++){
if(a[i][j]==0)
a[i][j]=m++;
}
for(int j=i+1;j<n-i;j++){
if(a[j][n-1-i]==0)
a[j][n-1-i]=m++;
}
for(int j=n-i-1;j>i;j--){
if(a[n-i-1][j]==0)
a[n-1-i][j]=m++;
}
for(int j=n-i-1;j>i;j--) {
if(a[j][i]==0)
a[j][i]=m++;
}
}
if(n%2)
a[n/2][n/2]=m;
}
int test2(){
const int n=10;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
a[i][j]=0;
spiral2(n);
for(int i=0;i<n;i++){
for(int j=0;j<n;j++)
cout<<setw(3)<<a[i][j]<<' ';
cout<<endl;
}
}
int main(){
test2();
}
输出:
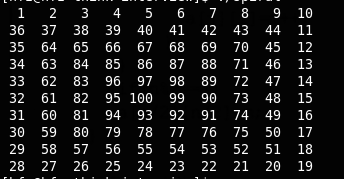
19. 概率问题

测试代码如下:
 View Code
View Code
#include <cstdlib>
using namespace std;
int main(){
const int Loop=1000;
const int R=100;
for(int i=0;i<=500;i++){
int rgn=0;
for(int j=0;j<Loop;j++){
int x=rand()%R;
int y=rand()%R;
if(x*x+y*y<R*R)
rgn++;
}
cout<<rgn<<' ';
if((i+1)%20==0)
cout<<endl;
}
}
输出如下:

20. 虚函数,覆盖问题
这儿牵扯到一个虚函数的使用问题,这儿没有使用基类的指针或基类引用,但是却利用虚函数实现了多态机制。
代码如下:
 View Code
View Code
using namespace std;
class A{
protected:
int m_data;
public:
A(int data=0):m_data(data){}
int GetData(){
cout<<"A-1 ";
return doGetData();
}
int virtual doGetData(){
// int doGetData(){
cout<<"A-2 ";
return m_data;
}
};
class B:public A{
protected:
int m_data;
public:
B(int data=1):m_data(data){}
int doGetData(){
cout<<"B-2 ";
return m_data;
}
};
class C:public B{
protected:
int m_data;
public:
C(int data=2){
m_data=data;
}
};
int main1(){
C c(10);
cout<<c.GetData()<<endl;
cout<<c.A::GetData()<<endl;
cout<<c.B::GetData()<<endl;
cout<<c.C::GetData()<<endl;
cout<<c.doGetData()<<endl;
cout<<c.A::doGetData()<<endl;
cout<<c.B::doGetData()<<endl;
cout<<c.C::doGetData()<<endl;
return 0;
}
class AA{
public:
virtual void f(){
cout<<"AA "<<endl;
}
};
class BB:public AA{
public:
void f(){
cout<<"BB "<<endl;
}
};
int main(){
AA* pa=new AA();
pa->f();
BB* pb=(BB*)pa;
pb->f();
delete pa,pb;
pa=new BB();
pa->f();
pb=(BB*)pa;
pb->f();
return 0;
}
该代码的输出如下:AA AA BB BB
21. 虚函数继承与虚继承

22. 多重继承 的优点与缺陷



23. C++所引入的额外开销








