基本排序算法 【转载】
基本排序算法
基于比较的排序
冒泡排序
没什么可说的, 改进方法就是加一个标志位防止有序后重复遍历. 由于需要遍历两次, 所以时间复杂度O(N^2)
- 传送门 --> 冒泡排序
选择排序
外层从0开始默认outer是最小数的下标, 内存从outer+1位置开始遍历, 不稳定, 如{ 3, 3, 3, 2 }, 当比较最后一个4时, 是第一个3和2交换, 从而不稳定. 内外层遍历两次, 时间复杂度O(N^2)
- 传送门 --> 选择排序
插入排序
相当于打扑克排序, outer从1到N-1, inner从outer到N-1, 时间复杂度O(N^2)
插入排序选择排序冒泡排序有浪费许多比较的次数
归并排序快的是因为小范围合并为大范围时, 有序可以同过外排方式
小组和为大组时, 组内有序没有浪费, 永远是组与组之间的比较
- 传送门 --> 插入排序
希尔排序
迄今为止, 除了在一些特殊的情况下, 还没人能够从理论上分析希尔排序的效率, 有各种各样基于实验的评估, 估计它的时间级从O(N^(3/2))到O(N^(7/6))
- 传送门 --> 希尔排序
归并排序
递归把一个数字分隔为两部分, T(N) = 2*T(N/2) + O(N), a= 2, b = 2, N = 1, 时间复杂度O(N*logN), 额外空间复杂度O(N)
递归符合master公式: T(N) = a*T(N/b) + O(N^d)时间复杂度为:
(1)log(b, a) > d --> 复杂度O(N^(log(b, a)))
(2)log(b, a) = d --> 复杂度O(N^d * logN)
(3)log(b, a) < d --> 复杂度O(N^d)
- 传送门 --> 归并排序
快排
递归公式同归并排序, 由于需要记录分隔点, 所以额外空间复杂度O(logN), 快排做不到稳定性, 因为partition过程做不到稳定
- 经典快排与数据状况有关, 这是因为分隔点选取的问题, 如{1, 2, 3, 4, 5, 6}分隔点选取最右边时每次只排序一个数字, 此时时间复杂度为O(N^2)
- 如果分隔点选取中位数, 则每次恰好可把数组划分为两部分, 时间复杂度为O(N*logN)
- 随机快排的分隔点随机选取, 把复杂度转化为与概率有关, 复杂度长期期望为O(N*logN)
- 传送门 --> 快排
堆排
大根堆结构重要两个函数heapInsert与heapify, 一个上浮, 一个是下沉, 优先级队列就是堆
建立堆的时间复杂度为O(log1) + O(log2) + O(log3) + ... + O(log(N)), 收敛域O(N)
- 算法: 插入时, 上浮, 直至没有父节点比当前节点大; 排序交换堆顶与堆未元素, 这时堆顶元素下沉, 直至当前节点比子节点都大
- 传送门 --> 堆排
排序补充
- 归并排序可以做到额外空间复杂度O(1), 有难度, 相关搜索"归并排序内部缓存法"
- 快排可以做到稳定性, 有难度, 不要求掌握, 相关搜索"01 stable sort"; 快排的优势是partition过程中, 时间复杂度O(N), 空间复杂度O(1)
- 有一道题目, 奇数放在数组的左边边, 偶数放在数组右边, 要求原始的相对次数不变, 牛客练习 --> 调整数组顺序使奇数位于偶数前面
排序总结
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(N^2) |
O(N) |
O(N^2) |
O(1) |
稳定 |
| 选择排序 | O(N^2) |
O(N^2) |
O(N^2) |
O(1) |
不稳定 |
| 插入排序 | O(N^2) |
O(N) |
O(N^2) |
O(1) |
稳定 |
| 希尔排序 | O(N*logN) ~ O(N^2) |
O(N^1.3) |
O(N^2) |
O(1) |
不稳定 |
| 堆排序 | O(N*logN) |
O(N*logN) |
O(N*logN) |
O(1) |
不稳定 |
| 归并排序 | O(N*logN) |
O(N*logN) |
O(N*logN) |
O(N) |
稳定 |
| 快排 | O(N*logN) |
O(N * logN) |
O(N^2) |
O(logN) ~ O(N) |
不稳定 |
工程中的综合排序算法
基础类型很长时, 使用快排, 因为基础数据类型不要求稳定
复合数据类型长度很长时, 使用归并排序, 复合数据类型要求稳定
任何数据类型的数组长度很短(<60)时, 使用插入排序
非基于比较的排序
非基于比较的排序, 与被排序的样本的实际数据状况有很大关系, 所以实际中并不经常使用
桶排序
简单桶排序: 一个桶统计一个数, 大体思路同计数排序, 如果数据是期望平均分布的,则每个桶中的元素平均个数为N/M, 最后一个for循环时间复杂度M*N/M, 所以总的时间复杂度O(N), 空间复杂度O(M+N). 头结点处理的挺漂亮, 其实就是计数排序.
- 传送门 --> 简单桶排序
桶排序: 一个桶统计一个范围内的数然后桶内排序.
如果数据是期望平均分布的, 则每个桶中的元素平均个数为N/M. 如果对每个桶中的元素排序使用的算法是快速排序, 每次排序的时间复杂度为O(N/Mlog(N/M)). 则总的时间复杂度为O(N)+O(M)O(N/Mlog(N/M)) = O(N+ Nlog(N/M)) = O(N + NlogN - NlogM) 当M接近于N是, 桶排序的时间复杂度就可以近似认为是O(N)的, 就是桶越多, 时间效率就越高, 而桶越多, 空间却就越大, 由此可见时间和空间是一个矛盾的两个方面
- 传送门 --> 桶排序
计数排序
时间复杂度先遍历数组求最大值最小值O(N), 然后加入桶O(N), 再累加桶O(M), 最后遍历原始数组O(N), 所以总的时间复杂度O(M+N), 当M=N时时间复杂度O(N), 空间复杂度O(N+K), M为数字的范围, 稳定
- 传送门 --> 计数排序
基数排序
其实利用计数排序的稳定性原理
- 传送门 --> 基数排序
二分查找
- 传送门 --> 二分查找
数组
出现频率最高的前k个元素
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
- 算法: 使用优先级队列, 类中重载小于号
priority_queue<ClassType>, 类外使用struct重载括号priority_queue<ClassType, vector<ClassType>, comparator> - leetcode --> 347.前K个高频元素
一个有序数组A, 另一个无序数组B, 打印B中所有不在A中的数组, A数组长度为N, B数组长度为M
- 算法1: 暴力法, 时间复杂度O(N^2)
- 算法2: 遍历B数组, 使用二分法在A中查找相同元素, 时间复杂度
O(M * logN) - 算法3: 把A数组进行排序, 排序最小时间复杂度
O(M*logM), 使用类似外排进行排序, 总时间复杂度O(M*logM) + O(M+N)
两个游标, p1指向A, p2指向B
(1) A[p1] < B[p2]; p1++
(2) A[p1] == B[p2]; p1不移动, 移动p2, 因为B数组中可能有重复数字所以只移动p2
(3) A[p1] > B[p2]; 打印并移动p2
- 传送门 --> 时间复杂度理解
搜索旋转排序数组
假设按照升序排序的数组在预先未知的某个点上进行了旋转
- 算法: 二分法. 循环内首先要先判断两个端点是否为target. arr[L]<arr[mid]: 说明左端有序右端无序, 进而判断target在不在左端范围内, 同理arr[L]>arr[mid]: 说明右端有序而左端无序, 进而判断在不在右端范围内
- LeetCode --> 33.搜索旋转排序数组
Pow(x, n)
- 算法: 还是二分法, 折半法
- leetcode --> 50.Pow(x, n)
使用递归查找数组中的最大值
- 算法: 二分法查找分隔数字, 返回左右数组中的最大值
本算法中T(N) = 2*T(N/2) + O(1), a=b=2, d=0, log(2, 2)=1 > d=0, 复杂度为O(N^log(2, 2))=O(N) - 传送门 --> 使用递归查找最大值
小和
在一个数组中, 每一个数左边比当前数小的数累加起来, 叫做这个数组的小和. 求一个数字的小和. 如[1, 3, 4, 2, 5]小和为16
- 算法: 归并排序变形, merge时把数组从小到大排列, 关键步骤
res += (arr[lowPtr] < arr[hightPtr] ? arr[lowPtr] * (right - hightPtr + 1) : 0);其中arr[lowPtr] * (right - hightPtr + 1)是关键, 和归并排序一样, 没有浪费之前的比较次数
本题递归公式T(N) = 2*T(N/2) + O(N), 时间复杂度同归并排序, 同位O(N*logN) - 传送门 --> 小和
逆序对
在一个数组中, 左边的数如果比右边的数大, 则这两个数构成一个逆序对, 请打印所有逆序对
- 算法: 与小和相同, 只是在merge时把数组从大到小排列, 关键步骤
res += (vt[leftPtr] > vt[rightPtr] ? (right - rightPtr + 1) : 0);与上述相差大小号和乘一个数区别, 目前只能统计个数, 打印有些问题 - 传送门 --> 逆序对
- 牛客 --> 数组中的逆序对
荷兰国旗问题
给定一个数组arr, 和一个数num, 请把小于num的数放在数组的左边, 等于num的数放在数组的中间, 大于num的数放在数组的右边, 要求额外空间复杂度O(1), 时间复杂度O(N)
- 算法: 准备三个游标leftPtr初始指向数组边界起始位置前一个元素即left-1, rightPtr初始指向末尾后一个元素right+1, index从头到尾遍历数组比较
(1) 比num小, index指向元素和leftPtr指向的下一元素交换, index和leftPtr同时+1
(2) 等于num, 只把index+1
(3) 大于num, 把index元素和rightPtr指向的元素前一个交换, rightPtr-1, 由于不确定rightPtr指向元素和num的关系, index不变
- 传送门 --> 荷兰国旗问题
移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
- 算法1: 与荷兰国旗类似, 这里准备两个指针, L指向左边边界数字与0交界数, 游标cur遍历数组
- 算法2: 使用algorithm中的remove方法, 然后遍历至从remove返回迭代的位置开始至数组尾部置0
- leetcode --> 283.移动零
求无序数组排序后相邻俩数最大差值
给定一个数组, 求排序之后相邻两数的最大差值, 要求时间复杂度O(N), 且要求使用非基于比较的排序
- 算法: 运用桶的概念. N个数, 准备N+1个桶, 最小值放0号桶, 最大桶放N号桶放N号桶;
三个数组, 分别记录桶是否有值, 桶内最大值, 桶内最小值; 相邻两个数最大差值可能存在于两个非空桶之间, 也可能存在于空桶之间 - 传送门 --> 排序数组最大差值
数据流中位数
如何可以得到数据流中排序后的中位数
用数组结构实现大小固定栈
- 传送门 --> 数组实现大小固定的栈
用数组结构实现大小固定队列
- 算法: 使用三个变量: start, end, size. 目的是为了是start和end解耦合, 使start只与size有关, end只与size有关.
插入只与m_size和m_arraySize有关, 弹出只与m_size和0有关; 弹出直接弹出m_start位置的元素, 插入直接插入到m_end位置
m_start的变化只与m_arraySize有关; m_end的变化只与m_arraySize有关. m_start与m_end都是+1递增 - 传送门 --> 数组实现大小固定的队列
大楼轮廓
给定一个N行3列二维数组, 每一行表示有一座大楼, 一共有N座大楼. 所有大楼的底部都坐落在X轴上, 每一行的三个值(a,b,c)代表每座大楼的从(a,0)点开始, 到(b,0)点结束, 高度为c. 输入的数据可以保证a<b,且a, b, c均为正数. 大楼之间可以有重合. 请输出整体的轮廓线
例子: 给定一个二维数组{{1, 3, 3}, {2, 4, 4}, {5, 6, 1}}, 输出轮廓线{{1, 2, 3}, {2, 4, 4}, {5, 6, 1}}
- 算法: 使用两个红黑树htMap和pmMap, htMap键为高度, 值高度出现的次数, pmMap记录当前位置最大轮廓, 键为位置, 值为高度. 利用红黑树自动排序功能, count只返回0或1, 不是返回出现次数!!!
- 传送门 --> 大楼轮廓
- LintCode --> 大楼轮廓
买卖股票的最佳时机含手续费
- 算法: 对于第i天的最大受益分成两种情况:
(1) 当天结束后手里 有 stock. 可能保持前一天的状态, 也可能是今天卖出的. cash
(2) 当天结束后手里 没有 stock. 可能保持前一天的状态, 也可能是买入了. hold
- 传送门 --> 714.买卖股票的最佳时机含手续费
未排序正数数组中累加和为给定值的最长子数组
给定一个数组arr, 该数组无序, 但每个值均为正数, 再给定一个正数k. 求arr的所有子数组中元素累加和为k的最长子数组
- 算法: 两个点, 利用都是正数的特点. 时间复杂度O(N), 空间复杂度O(1)
- 传送门 --> 未排序正数数组中累加和为给定值的最长子数组
未排序数组中累加和为给定值的最长子数组
给定一个数组arr, 数组有正有负, 和一个整数aim, 求在arr中, 累加和等于aim的最长子数组的长度
- 算法: 若数组累加和为sum, 找到子数组中第一次出现sum-aim值的位置, 则从此位置之后到数组结尾就为所求最长子数组. 时间复杂度O(N), 空间复杂度O(N)
map中记录累加和第一次出现的位置, 累加和0为-1位置(一个数都没有的情况下也能累加出0), 查出位置是从累加和的下一位置到当前位置, 若不记录会错过从0开始的位置 - 传送门 --> 数组累加和
数组中都是整数, 有奇数有偶数, 求奇数与偶数个数相等的最长子数组
- 算法: 奇数记为1, 偶数记为-1, 求累加和为0的最长子数组
数组中含有0, 1, 2, 求子数组中含有1的数量和含有2的数量相等的最长子数组是多少
- 算法: 0还是0, 1还是1, 2变为-1, 求累加和为0的最长子数组
数组最多异或和划分
给定一个数组arr, 可以任意把arr分成很多不相容的子数组. 求: 分出来的子数组中, 异或和为0的子数组最多是多少
- 算法: 与 数组累加和等于aim最长子数组 类似, 都是用一个map记录数值出现位置, 前者记录最早出现的位置, 后者记录最近一次出现的位置
数据dp记录异或和的位置, 假设数组最后一个数的下标是i, 并且数组存在一个最优划分, 使得划分的子数组个数最多, 那么i有两种情况
(1) i所在的划分区间异或为0. --> dp[i] = dp[i-1]
(2) i所在的划分区间异或不为0, 假设i的最优划分区间是[k,i], 0到i的连续异或为sum, 之要求出一个最大的下标k-1, 使得0到k-1的异或也为sum就满足条件. --> dp[i]=dp[k]+1
(3) 由于求最多异或和, 所以dp[i]=max(dp[i-1], dp[i]);
- 传送门 --> 数组异或和
窗口内最大值数组
有一个整型数组arr和一个大小为w的窗口从数组的最左边滑到最右边, 窗口每次向右滑一个位置. 如果数组长度为n, 窗口大小为w, 则一共产生n-w+1个窗口的最大值. 实现一个函数. 输入: 整型数组arr, 窗口大小为w. 输出: 一个长度为n-w+1的数组res, res[i]表示每一种窗口状态下的数组
- 算法1: 暴力方法, 扣边界, 时间复杂度O(N*W);
- 算法2: 使用list(本算法中不需要随机访问, 所以不使用deque)qmax, 队列中保存数组的下标, 遍历数组, 时间复杂度O(N), 遍历数组, 每个数只会进队列一次, 出队列一次
(1)游标i大于等于数组qmax, 弹出尾部所有小于等于i的值, 这里之所以使用等于, 是为了更新值相等情况下的qmax中数组下标
(2)qmax.front() == i-w时, 弹出qmax头部, 因为此时该元素不在窗口内, 值已经过期 - 传送门 --> 窗口内最大值数组
最大值减去最小值小于或等于num的子数组数量
给定数组arr和整数num, 共返回有多少个子数组(连续)满足如下情况:
max(arr[i..j]) - min(arr[i..j]) <= num
max(arr[i..j])表示子数组arr[i..j]中的最大值, min(arr[i..j])表示子数组arr[i..j]中的最小值
要求: 数组长度为N, 实现时间复杂度为O(N)的解法
- 算法1: 暴力解O(N^3), 生成的子数组共O(N^2), 每个子数组求最大最小值O(N), 所以总时间复杂度共O(N^3)
- 算法2: 利用两个思路可以加速: (1) 一个子数组达标, 数组内任何子数组都达标; (2) 一个子数字不达标, 数组外任何子数组都不达标. 相当于使用两个滑动窗口, 一个窗口保存最大值, 一个窗口保存最小值
- 传送门 --> 最大值减去最小值小于或等于num的子数组数量
单调栈结构
解决数组中所有数, 左边距离它最近比它小/大的数, 右边距离它最近比它小/大的数. 要求O(N)
- 算法1: 暴力解, 依次遍历每个元素, 再遍历这个元素的两边时间复杂度O(N^2)
- 算法2: 使用栈使用单调栈结构(栈中保存数组的下标), 遍历每个元素, 压栈过程中从小到大(从大到小)压栈. 若有重复元素, 栈中元素使用链表. 每个数进入/弹出一次, 时间复杂度O(N)
(1)使栈中元素弹出的元素即为最右边最小(大)值, 栈中剩余元素为最左边最小(大)值
(2)依次弹出栈, 栈的左边元素为下以元素, 右边元素为-1 - 传送门 --> 单调栈结构
最大子矩阵
给定一个整型矩阵map, 其中的值只有0和1两种, 求其中全是1的所有矩形区域中, 最大的矩形区域为1的数量
例如: {1, 1, 1, 0} = 3; {{1, 0, 1, 1}, {1, 1, 1, 1}, {1, 1, 1, 0}} = 6
- 算法: 运用值方图的概念, 分别以每一行为底做值方图数组, 求值方图的最大值. 时间复杂度O(M*N)
- 传送门 --> 最大子矩阵
矩阵
顺时针打印矩阵
给定一个整型矩阵matrix, 按照从外向里以顺时针的顺序依次打印出每一个数字. 例如:如果输入如下4 X 4矩阵: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.
旋转正方形
给定一个整型正方形矩阵matrix, 把该矩阵调整成顺时针转换90度的样子. 额外空间复杂度O(1)
- 算法: 同顺时针打印矩阵一样, 抽象一个顺时针打印边框的函数, 从外到内依次调用这个函数.
- 传送门 --> 旋转正方形矩阵
之字形打印矩阵
给定一个矩阵matrix, 按照"之"字形方式打印这个矩阵
- 算法: 抽象一个打印斜行的矩阵, 通过一个布尔变量来判断从上到下还是从下到上, 调用函数多了些边界判断. x_1和y_1, x_2和y_2先后移动次序有很大关系, 先比较x_1再判断y_1, 先比较y_2再判断x_2,
- 传送门 --> 之字形打印矩阵
行列有序的矩阵中查找
给定一个由N*M的整数型矩阵matrix和一个整数K, matrix的每一行和每一列都是排好序的. 实现一个函数, 判断K是否在matrix中. 要求时间复杂度O(N+M), 额外空间复杂度O(1)
- 算法: 从矩阵的特性出发, 确定查找方法. 设置查找起始点设置为右上角
(1)若K小于右上角的数, 则不可能在当前列的下面, 左移起始点
(2)若K大于右上角的数, 则不可能在当前行的左边, 下移起始点 - 传送门 --> 行列有序的矩阵中查找
- 牛客 --> 二维数组中的查找
最小路径和
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
- 算法1: 暴力递归, 注意边界条件. 递归公式Path(m, n) = grid[m][m] + min(Path(m + 1, n), Path(m, n + 1))
- 算法2: 根据递归暴力递归改动态规划
- leetcode --> 64.最小路径和
岛问题
一个矩阵中只有0和1两种值, 每个位置都可以和自己的上行左右四个位置相连, 如果有一片1连在一起, 这个部分叫做一个岛, 求一个矩阵中有多少个岛
- 算法: 按顺序遍历矩阵, 每遍历一个点都判断这个节点是否被遍历过
- 传送门 --> 岛问题
判断在一个矩阵中是否存在一条包含某字符串所有字符的路径
- 算法: 路径可以向上、向下、向左、向右走, 利用递归做好边界条件的判断
- 牛客 --> 矩阵中的路径
水位上升的泳池中游泳
- 算法: 矩阵中字符匹配类似. 这里多一步二分法查找, 这个二分法查找有意思, minVal <= maxVal, 这里等号不能去掉, 当maxVal不满足, 而maxVal+1满足时, 里面的if循环会把minVal=maxVal时再+1
- leetcode --> 778.水位上升的泳池中游泳
队列栈
仅用队列结构实现栈结构
- 算法: 使用两个队列, m_queue, m_help, pop与top操作需要把m_queue中元素弹出并压进m_help中直至剩最后一个元素, pop则把最后一个元素丢弃, push则把最后一个元素插入m_help中, 然后交换m_queue与m_help指针
- 传送门 --> 仅用队列结构实现栈
仅用栈结构实现队列结构
- 算法: 使用两个栈, m_push与m_pop分别对应push与pop操作, 当m_pop栈为空时, 把m_push栈中的所有元素弹出并压进m_pop栈中
- 传送门 --> 栈结构实现队列结构
- 牛客 --> 用两个栈实现队列
双栈返回最小值
实现一个特殊的栈, 在实现栈的基本功能的基础上, 再实现返回栈中的最小元素的操作. 要求: 1. pop, push, getMin操作的时间复杂度都是O(1); 2. 设计的栈类型可以使用现成的栈结构
逆序栈
逆序栈, 不能申请额外的数据结构, 只能使用递归函数
- 算法: 利用两个递归函数, 一个用来逆序栈, 一个用来获得栈底元素.
- 传送门 --> 逆序栈
链表
链表问题往往在空间复杂度上下工夫, 时间复杂度基本是O(N)或O(N^2)
笔试: 目的最快把问题过掉, 不追求空间复杂度
面试: 和面试官聊空间复杂度
快慢指针的while循环: ptrFast=ptrSlow=head; while((ptrFast->next != nullptr) && (ptrFast->next->next != nullptr));
遍历结束时: 偶数个元素, 慢指针走都中间两个元素前一个元素; 奇数个元素, 慢指针恰好走到中间元素
链表中倒数第k个结点
输入一个链表, 输出该链表中倒数第k个结点
- 算法: 两个节点一个节点先走, 另一个节点等k个循环之后再走. 边界扣定问题
- 传送门 --> 链表中倒数第k个结点
- 牛客 --> 链表中倒数第k个结点
分别实现反转单向链表和反转双向链表函数
- 算法: 分别定义两个指针, next和pre, 当head不为空时, pre初始化为nullptr
- 翻转单链表4步: (1) next=cur->next; (2) cur->next=pre; (3) pre=cur; (4) cur=next;
- 翻转双链表4+1步: (1) next=cur->next; (2) cur->next=pre; (2+1) cur->pre=next; (3) pre=cur; (4) cur=next;
判断一个链表是否是回文结构
给定一个链表的头结点head, 判断该链表是否是会问结构. 如: 1, 2, 1返回true; 1, 2, 2, 1返回true; 1, 2, 3返回false. 如果求时间复杂度O(N), 额外空间复杂度O(1)
- 算法1: 使用栈把元素逆序, 遍历两次列表, 第一次压栈, 第二次和栈中元素对比是否相同, 时间复杂度O(N), 额外空间复杂度O(N)
- 算法2: 使用快慢指针. 时间复杂度O(N), 需要N/2个额外空间
- 算法3: 快慢指针+反转链表. 时间复杂的O(N), 额外空间复杂度O(1). 翻转链表时假定头部节点为要翻转节点的下一节点, 相当于prePtr的位置指定为要翻转的节点, 处理ptrPtr的next域指向空(因为翻转后是尾节点要指向nullptr)
- 传送门 --> 判断一个链表是否是回文结构
单向链表划分
将单向链表按某值划分成左边小, 中间相等, 右边大的形式
- 算法1: (1)准备一个数组存放node节点, 然后遍历链表把结点都放入数组中;(2)根据数组中的元素对数组进行划分;(3)之后从头到尾恢复链表, 时间复杂度O(N), 额外空间复杂度O(N), 不稳定
- 算法2: 准备6个指针, 分别存放小于, 等于, 大于pivot的节点, 关键在于最后这6个指针的连接, 扣边界
- 传送门 --> 单向链表划分
复制含有随机指针节点的链表
输入一个复杂链表(每个节点中有节点值, 以及两个指针, 一个指向下一个节点, 另一个特殊指针指向任意一个节点), 返回结果为复制后复杂链表的head. (注意, 输出结果中请不要返回参数中的节点引用, 否则判题程序会直接返回空)
- 算法1: 使用哈希表, 表的key为要复制的节点, value为复制后的节点. 遍历两次, 第一次建立节点, 第二次连接next指针和rand指针
- 算法2: (1)克隆每个节点, 并在被克隆的节点之口插入该克隆结点, 被克隆节点与克隆节点相邻; (2)并且克隆节点的random指针位置正好在被克隆节点random指针的下一位置, 这样刚好可以通过被克隆节点的random指针指向克隆节点random指针的位置. 拆开链表时扣边界挺有意思
curCopy->next = (next != nullptr ? next->next : nullptr); - 传送门 --> 复制含有随机指针节点的链表
- 牛客 --> 复杂链表的复制
判断单链表是否有环
- 算法1: 哈希表, 边遍历变查找, 使用set容器和find函数
- 算法2: 使用快慢指针, 快慢指针相遇后, 快指针从head从重新开始遍历, 一次走一个节点
x为环前面的路程(黑色部分), a为环入口到相遇点的路程(蓝色部分, 假设顺时针走), c为环的长度()(蓝色+红色部分).
快慢指针相遇时慢指针走的路程s1=x+m*c+a, 快指针走的路程s2=x+n*c+a, 2s1=s2 --> 2*(x+m*c+a)=(x+n*c+a), 得x=(n-2*m)*c-a=(n-2*m-1)*c+c-a
即环前面的路程 = 数个环的长度 (为可能为0) + c - a
c-a是相遇点后, 环后面部分的路程(红色部分)
所以, 可以让一个指针从起点A开始走, 让一个指针从相遇点B开始继续往后走
2个指针速度一样, 那么, 当从原点的指针走到环入口点的时候(此时刚好走了x)
从相遇点开始走的那个指针也一定刚好到达环入口点, 所以2者会相遇, 且恰好相遇在环的入口点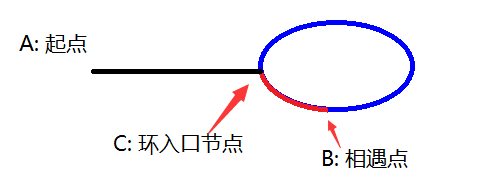
无环单链表相交问题
- 算法1: 使用哈希表, 先遍历一个链表插入哈希表中, 使用unordered_set容器和find函数; 遍历第二个链表并比较哈希表中的节点, 若遍历到尾则无相交节点
- 算法2: 遍历两个链表得到尾节点地址和链表节点数分别为end1, len1, end2, len2, 若end1=end2, 让一个指针先走(len1-len2)个节点即为入口
- 传送门 --> 无环单链表相交问题
- 牛客 --> 两个链表的第一个公共结点
两个链表相交问题
实现一个函数, 如果两个链表相交, 返回相交的第一个结点, 如果不相交返回nullptr. 如果链表1长度N, 链表2长度M, 要求时间复杂度O(M+N), 额外空间复杂度O(1)
- 算法: 步骤: (1)判断单链表有环无换; (2)判断无环单链表第一个相交的节点; (3)判断有环链表第一相交的节点
有环链表相交共三种情况: (1)各自有环不相交; (2)相交后共享一个环; (3)有环, 两个链表入口节点不同
(1) loop1=loop2时, 第二中情况. 转化到两个无环链表, 找第一相交节点
(2) loop!=loop2时, loop1不断next方向往下走. 情况3, 遇到loop2; 情况1, 没遇到loop1
- 传送门 --> 两个链表相交问题
缓存算法
LRU(Least Recently Used, 最近最少使用)
设计一种缓存结构, 该结构在构造时确定大小, 假设大小为K, 并有两个功能:
(1)set(key,value): 将记录(key,value)插入该结构;
(2)get(key): 返回key对应的value值
要求: (1)set和get方法的时间复杂度为O(1); (2)某个key的set或get操作一旦发生, 认为这个key的记录成了最经常使用的; (3)当缓存的大小超过K时, 移除最不经常使用的记录, 即set或get最久远的
- 算法: 时间复杂度O(1)自然使用哈希表保存记录, 可更新链表与双向链表类似, 哈希表与双向链表组合. 使用keyNodeMap用于从key到value映射对应get方法, nodeKeyMap保存从value到key的映射, 用于更新链表时查找node对应的key
- 传送门 --> LRU
二叉树
二叉树的遍历
- 递归版: 每个节点都会走过三次, 只是走过节点时的打印时机不同. (1) 先序, 在第一次经过节点时就会打印其值; (2) 中序, 在第二次经过该节点打印其值; (3) 后序, 在最后一次经过该节点时会打印其值
- 非递归版:
(1)先序: 使用一个栈, 令一个游标等于头节点并压栈. 当栈不为空时, 由于栈是先进后出要先打印左节点, 就要先压右节点然后再压左节点
(2)中序: 使用一个栈, 令一个游标等于头节点. 当栈不为空且游标不为nullptr时while ((!sk.empty()) || (cur != nullptr)), head不为空压栈, 游标左移; head为空弹出栈打印, 游标右移. 总结下, 就是先跑左边, 左边跑完再跑右边, 跑右边时弹出堆栈并打印
(3)后序: 两种方法(1)双栈结构, 同先序, 区别是先压左节点再压右节点; (2)使用一个栈, 用一个指针保留最近处理过的节点 - 传送门 --> 二叉树的遍历
二叉树的镜像
二叉树的前驱与后继节点
后继: 该节点中序遍历的下一个节点
前驱: 该结点中序遍历的前一个节点
- 前驱算法: (1)有左子树, 返回左子树的最右边节点; (2)无左子树, 非右孩子: 查找该节点是以哪个节点为子树的最左边节点; 右孩子: 返回父节点
- 后继算法: (1)有右子树, 返回右子树的最左边节点; (2)无右子树, 非左孩子: 查找该结点是以哪个节点为子树的最右边节点; 左孩子: 返回父节点
- 传送门 --> 二叉树的前驱与后继节点
- 牛客 --> 二叉树的下一个结点
对称二叉树判断
- 算法: 利用二叉树的递归遍历. 不能使用中序遍历后的数组两端是否相等来进行判断, 例如节点数相同1的任意树结构. 不能使用一个节点的递归, 下层非对称上层可以是对称的, 不能利用下层返回信息来判断上层结构
- 传送门 --> 对称二叉树判断
- 牛客 --> 对称的二叉树
二叉树的深度
判断一课二叉树是否是搜索二叉树
一个二叉搜索树具有如下特征
- 节点的左子树只包含小于当前节点的数.
- 节点的右子树只包含大于当前节点的数.
- 所有左子树和右子树自身必须也是二叉搜索树.
- 算法1: 二叉树中序遍历非递归版打印部分加些代码
- 算法2: morris遍历, 待解决
- 算法3: 只判断当前节点的左孩子与右孩子了, 并没有判断整颗左子树与右子树中的最大值与最小值和当前节点是否满足二叉搜索树的条件, 待完善
- 传送门 --> 判断一课二叉树是否是搜索二叉树
- leetcode --> 98. 验证二叉搜索树
判断一颗二叉树是否是完全二叉树
- 算法: 二叉树的按层遍历, 增加一个标志位标识是否是叶子节点. 可分为两种情况进行处理:
(1)左孩子为空并且右孩子为空, 返回false
(2)左孩子不为空右孩子为空, 或者左右孩子都为空, 下次迭代开启叶子节点检查状态 - 传送门 --> 判断一颗二叉树是否是完全二叉树
按层打印二叉树
二叉树之字形打印
- 算法: 使用两个栈数组, 使用变量来代替数组下标的变化. 不能使用一个队列如把二叉树打印成多行那样, 因为本层多个节点时, 队列后面存储当前左右孩子相反时, 下层节点的先后顺序发生改变
- 传送门 --> 二叉树之字形打印
- 牛客练习 --> 按之字形顺序打印二叉树
二叉树的序列化与反序列化
目前版本只有先序方式的序列化与反列化
- 传送门 --> 二叉树的序列化与反序列化
- 牛客 --> 序列化二叉树
按层序列化二叉树
算法: 使用string字符串没有结束字符, 分隔后找不到结尾, 故统一每个节点后的分隔符为叹号. 反序列化的关键在于string的分隔, string的find使用方法是关键, 使用了string::npos
- 传送门 --> 按层序列化二叉树
完全二叉树节点的个数
要求: 时间复杂度低于O(N), N为这颗树的节点个数
- 算法: 利用二叉树的概念. 满二叉树高度L, 节点2^L-1个; mostLeftLevel找当前节点可到达的最大深度时, 节点下移, 层数同时+1. 每一层只会选择一个节点进行递归, 所以调用递归函数的次数为O(h). 每次调用递归函数都会查看node的最左节点, 所以会遍历O(h)个节点, 整个过程的时间复杂度O(h^2)
(1)由于是完全二叉树, 先遍历整颗树的左边界获取树高L
(2)遍历右子树的做边界是否到达最后一层:
(1)是, 当前节点的左子树是满的, 左子树的加当前节点的个数为2^L-1+1=2^L, 递归求右子树
(2)否, 当前节点的右子树是满的, 右子树加当前节点的个数为2^(L-1)+1-1=2^(L-1), 递归求左子树
复杂度: 每层只遍历一个节点, 共有O(logN)层, 每个子树的左边界O(logN), 总的时间复杂度: O((logN)^2) - 传送门 --> 完全二叉树节点的个数
二叉树中和为某一值的路径
输入一颗二叉树的根节点和一个整数, 打印出二叉树中结点值的和为输入整数的所有路径. 路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径.
- 算法: 宽度优先, vector弹出与压出
- 传送门 --> 二叉树中和为某一值的路径
- 牛客练习 --> 二叉树中和为某一值的路径
二叉树重建
输入二叉树先序遍历和中序遍历结果, 重建二叉树
- 算法 --> 根据先序和中序重建二叉树
- 牛客练习 --> 重建二叉树
判断t1树中是否有与t2树拓扑结构完全相同的子树
给定彼此独立的两颗树头结点分别为t1和t2, 判断t1中是否有与t2树拓扑结构完全相同的子树
- 算法: 把树序列化, 使用KMP字符串匹配算法, 查看T2的序列化结果是否是T1的子串
- 传送门 --> 拓扑结构完全相同的子树
判断t1树是否包含t2树的全部的拓扑结构
给定彼此独立的两颗树头结点分别为t1和t2, 判断t1树是否包含t2树全部的拓扑结构
- 算法: 使用两个递归函数, 一个判断是否结构相同, 一个判断当结构不同时, 移动t1的指针进行, 判断t1的子树是否包含t2的结构. 二叉树递归返回与或非的示例
- 传送门 --> 判断t1树是否包含t2树的全部的拓扑结构
在二叉树中找到两个节点的最近公共祖先
给定一课二叉树的头结点head, 以及这颗树中的两个节点o1和o2, 返回o1和o2的最近公共祖先节点
- 算法1: 利用二叉树的后续遍历, 后续遍历结束相当于处理完两颗子树会返回所需信息, 实际就是利用后续遍历分别查找两个节点. 假设处理cur时左子树返回节点L, 右子树返回节点R
(1)如果cur等与nullptr, 或者等于p1或p2, 返回cur. -->找到节点了
(2)如果L和R都为nullptr, 说明cur左右子树都没有出现过p1或p2, 返回nullptr
(3)如果L和R都不为nullptr, 说明在cur的两颗子树都分别发现过p1和p2, 返回此时的cur
(4)如果L和R中有一个为nullptr, 一个不为nullptr, 此时有两种情况, 要么cur是p1或p2之中一个, 要么cur已经是p1和p2的最近公共祖先. 无论那种情况直接返回nullptr - 算法2: 构建一个表. 遍历树, 使用map记录每个节点的父节点, 然后通过这个map把从根节点至p1所有的节点插入set中, 同理, p2利用这个map中祖先节点到set中查找, 找到就挺
- leetcode --> 236. 二叉树的最近公共祖先
二叉树之递归极好用
二叉树中的最大路径和
给定一个非空二叉树,返回其最大路径和。
- 算法: 利用递归, 先处理左子树, 再处理右子树, 其中利用一个全局变量记录返回值. 这里基本递归返回0做基值
- 传送门 --> 124.二叉树中的最大路径和
判断一颗二叉树是否是平衡树
以每个节点作为头结点的树都是平衡树则整颗树平衡.
- 算法1: 设计递归返回结构, 返回两个信息: (1) 是否平衡; (2) 返回高度. 整个递归过程按照同样的函数得到子树的信息, 整合子树的信息, 加工出我的信息向上返回, 要求返回结构一样. 使用了智能指针
- 算法2: 使用递归计算树高. 平衡信息作为返回值, 树高作为传出参数. 太神奇了
- 算法3: 树高做传入参数来进行处理, 多看几遍
- 传送门 --> 判断一颗二叉树是否是平衡树
- 牛客 --> 平衡二叉树
最大搜索二叉子树
给定一棵二叉树的头节点head, 请返回最大搜索二叉子树的大小
- 算法: 求每一个节点为头的整颗树的最大搜索二叉树. 情况分析
1.左树最大搜索二叉树
2.右树最大搜索二叉树
3.左树最大搜索二叉树头部, 是当前节点左孩子
4.右树最大搜索二叉树头部, 是当前节点右孩子
满足3, 4情况下, 求左树最大值与右树最小值, 并与当前节点比较 - 设计递归返回结构: (1)左搜大小; (2)右搜大小; (3)左搜头; (4)右搜头; (5)左max; (6)右min
- 精炼递归返回结构: (1)搜大小; (2)搜头; (3)min, max
- 传送门 --> 最大搜索二叉子树
二叉树最远距离
二叉树中, 一个节点可以往上走和往下走, 那么从节点A总能走到节点B. 节点A走到节点B的距离为: A走到B最短路径上的节点个数. 求一棵二叉树上的最远距离
- 算法: 求每一个节点为头的整颗树的最大距离. 情况分析:
1.以当前节点为头的整颗树最大距离来自左子树最大距离, 不经过当前节点
2.以当前节点为头的整颗树最大距离来自右子树最大距离, 不经过当前节点
3.经过当前节点, 当前节点到两个节点深度和 - 设计递归返回结构: (1)左子树最大距离; (2)右子树最大距离; (3)左子树深度+右子树深度
- 精炼递归返回结构: (1)最大距离; (2)深度
- 传送门 --> 二叉树路径
公司活跃度
一个公司的上下节关系是一棵多叉树, 这个公司要举办晚会, 作为组织者已经摸清了大家的心理: 一个员工的直接上级如果到场, 这个员工肯定不会来. 每个员工都有一个活跃度的值, 决定谁来你会给这个员工发邀请函, 怎么让舞会的气氛最活跃? 返回最大的活跃值
举例: 给定一个矩阵来表述这种关系, matrix ={ {1,6}, {1,5}, {1,4} }, 这
个矩阵的含义是:
matrix[0] = {1 , 6}, 表示0这个员工的直接上级为1, 0这个员工自己的活跃度为6
matrix[1] = {1 , 5}, 表示1这个员工的直接上级为1(他自己是这个公司的最大boss), 1这个员工自己的活跃度为5
matrix[2] = {1 , 4}, 表示2这个员工的直接上级为1, 2这个员工自己的活跃度为4
为了让晚会活跃度最大, 应该让1不来, 0和2来. 最后返回活跃度为10
- 算法: 情况分析:
1.直接领导来, 员工肯定不来
2.直接领导不来, 员工可分为来或不来, 取最大值 - 设计返回结构: (1)来时的活跃度; (2)不来时活跃度
- 传送门 --> 公司活跃度
哈希
- 经典哈希函数输入域无穷大
- 哈希函数的输出域有穷尽
- 输入一样, 输出肯定一样
- 输入不一样, 输出可能一样, 即哈希碰撞
- 输出域均匀分布. 输出结果模m, 结果0~m-1均匀分布
哈希函数可以打乱输入规律
特征: (1)与输入规律无关; (2)输出结果模m, 结果0~m-1均匀分布
急需1000个哈希函数(相对独立), 可以通过1个哈希函数来获得
比如哈希函数h, 会得到2^64范围, 16字节字符串, 得到结果分为高8位h1与低8位h2
可以得到哈希函数h3=h1+1*h2, h4=h1+2*h2, ...通过改变系数获得多个哈希函数
哈希表: 利用哈希函数做一N桶, 在桶中挂一些链. 哈希表的增删改查可以理解成时间复杂度O(1), 但实际不是, 有扩容代价, 哈希表扩容, 离线扩容
100T大文件, 每行是一个字符串, 打印所有重复的字符串. 思路: 通过哈希分流
问: 给多少台机器. 机器标号如1000台, 标号0~999
问: 大文件存在哪
问: 处理大文件按行读是否有很快的读取工具
把每一行作为文本读出来, 利用哈希函数计算一个哈希code, 然后模1000, 模的结果是多少就存放在多少号的机器上. 相同的文本一定会分配到一台机器上, 如果有重复的文本一定会来到一台机器上, 出现的不同字符串(相同字符串算一种)
布隆过滤器
不安全网页的黑名单包含100亿个黑名单网页, 每个网页的URL最多占用64B. 现在想要实现一个网页过滤系统, 利用该系统可以根据URL判断该网页是否在黑名单上, 设计该系统
要求: 该系统允许有万分之一以下的判断失误率; 使用的额外空间不超过30GB
思路1: 先前如大文件, 有些浪费空间, 还可以继续优化吗
思路2: 如果把黑名单中的所有URL通过数据库或哈希表保存下来, 就可以对每条URL进行查询, 但是每个URL有64B, 数量100亿个, 所以至少需要640GB空间, 不满足要求
准备一个长度为m的bit类型数组bitMap, 准备k个彼此独立的哈希函数(计算结果独立), 这些函数输出值域大于或等于m, 使用这k个哈希函数对一个url进行计算. 对每一结果都对m取余, 然后再bitMap中想应位置1. 按照同样方法处理所有黑名单中的对象, 遇到已经为1的位置保持不变
黑名单中样本的个数为100亿个, 记为n; 失误率不能超过0.001%, 记为p; 每个样本的大小为64B, 这个信息不会影响布隆过滤器的大小, 只和选择哈希函数有关, 一本的哈希函数都可以接受64B的输入对象, 所以使用布隆过滤器还有一个好处是不用顾忌单个样本的大小, 它丝毫不能影响布隆过滤器的大小
bit位数: m = -(n * lnp) / (ln2)^2
哈希函数个数: k = ln2 * (m / n)
m与k向上取整后失误率: (1 - e^(-(m*k)/m))^k
一致性哈希
数据迁移代价很低, 同时可以完成负载均衡
通过虚拟节点, 路由表映射虚拟节点
如何均匀洗牌
设计RandomPool
设计一种结果, 在该结构中有如下三个功能: insert(key)将某个key加入到该结构, 做到不重复加入. delete(key): 将原本在结构中的某个key移除. getRandom(): 等概率随机返回结构中的任何一个key
要求: insert, delete, getRandom方法的时间复杂度都是O(1). 貌似可以是红包系统, 插入金额, 发红包时随机返回钱数
- 算法:
(1)准备一个两个哈希表和一个size. 若一个, 则当样本小时, 不能做到严格等概率随机返回一个key, 若遍历则时间复杂度不再是O(1)
(2)map1: key存放值, value存放进入次序; map2: key存放进入次序, value存放值. 同过random函数随机一个0~size中的一个数, 在map2中把随机出来的数字返回, map2作用是查找一个index值是什么
(3)delete: 删除产生洞时, map2中使用最后一个元素填这个洞(为了使getRandom继续生效), 修改map1的最后一个插入元素的index为删除元素的index - 传送门 --> RandomPool
并查集
给定一个没有重复的整型数组arr, 初始认为arr中每一个数都各自是一个单独的集合. 设计一种结构, 提供isSameSet查询是否处于一个集合与unionSet合并集合. 要求: 如果调用isSameSet与unionSet的总次数逼近或者超过O(N), 做到单次调用isSameSet或unionSet方法的平均时间复杂度为O(1)
- 算法: 结构上如何避免重复, 以及合并完的部分不重复 --> 并查集. 并查集初始化时, 必须已知所有数据样本, 不能对于流样本处理
- 传送门 --> 并查集
岛问题升级
假设矩阵很大, 并有多个cpu, 怎么把这道题目分解. 设计一个分治的思路, 多任务并行的算法. 一个矩阵切四块, 各自块信息算好之后, 能不能合并正确的岛数; 或者设计一种思路, 可切任意块, 各自块算好之后合并正确的岛数, 关键在于岛的边界信息如何合并
如何避免重复, 以及合并完的部分不重复 --> 并查集
A|E: 不在一个集合, 合并得集合(A, E), -1
B|C: 不在一个集合, 合并得集合(B, C), -1
A|C: 不在一个集合, 合并得集合(A, B, C, E), -1
B|E: 在一个集合
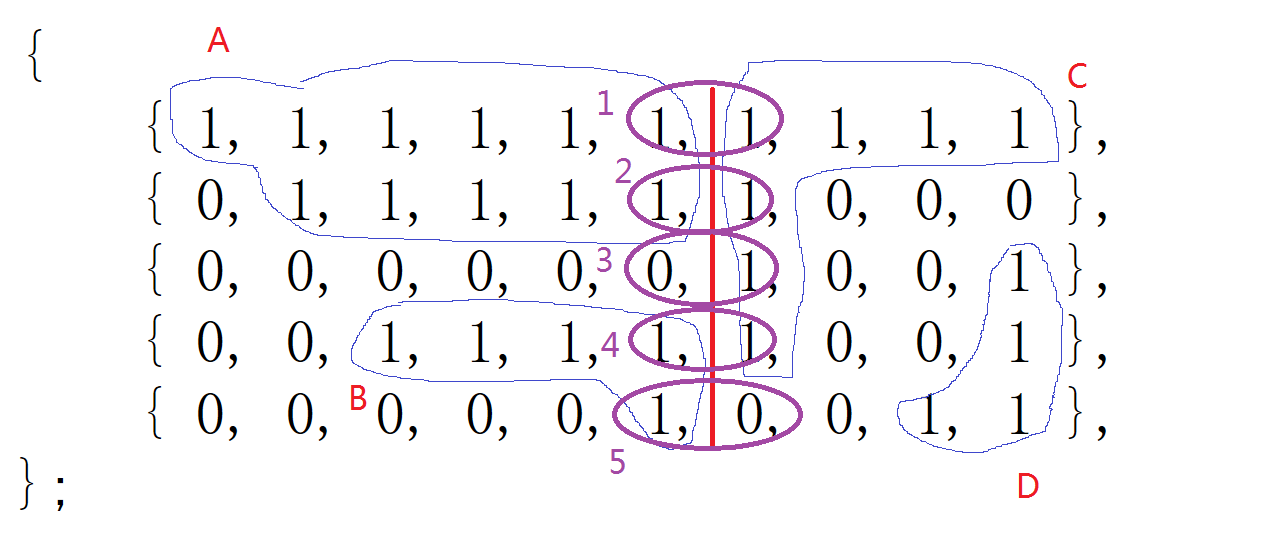
如图, 把矩阵按中间红色部分分为两块, 左边有岛A, B, 右边有岛C, D共4个岛, 合并
(1)交界1处, 1和1相交, 分别属于集合A, C, 合并集合得集合(A, B), 岛数量-1
(2)交界2处, 1和1相交, 属于一个集合(A, B)
(3)交界3处, 0和1相交, 跳过
(4)交界4处, 1和1相交, B与C不属于同一集合, 合并得集合(A, B, C), 岛数量-1
最终一共4-1-1=2个岛, 查找是否在一个集合可使用并查集
字符串
哈夫曼编码
每组数据一行, 为待编码的字符串. 保证字符串长度小于等于1000. 求这个字符串最短编码的长度
- 算法: 哈夫曼编码, 使用最小堆实现
- 传送门 --> 哈夫曼编码
字符串最小字典序拼接
"b", "ba"拼接, 按字典序排列之后是"bba", 实际"bab"字典序最小
排序策略有传递性
比较器: 甲乙丙
甲, 乙, 甲放前面
乙, 丙, 乙放前面
甲, 丙, 甲放前面
无传递性,
- 传送门 --> 字符串最小字典序拼接
最长对称字符串
给定的字符串里面, 找出最长的对称字符串(可以跳过部分字符)
- 算法: 两个游标分别指向头部和尾部, 思想就是要当前位置不要当前位置
- 传送门 --> 最长对称字符串
字符串子序列
打印一个字符串的全部子序列, 包括空字符串
- 算法: 与背包问题相似, 要当前的字符, 不要当前字符两种情况递归
- 传送门 --> 字符串子序列
字符串全排列
输入一个字符串(输入一个字符串,长度不超过9, 可能有字符重复, 字符只包括大小写字母), 按字典序打印出该字符串中字符的所有排列.
例如输入字符串abc, 则打印出由字符a, b, c所能排列出来的所有字符串abc, acb, bac, bca, cab和cba.
给定字符串构成最长回文字符串
给定一个包含大写字母和小写字母的字符串, 找到通过这些字母构造成的最长的回文串. 在构造过程中, 请注意区分大小写. 比如"Aa"不能当做一个回文字符串
- 算法: 回文字符串中出现奇数的字符一定在中间, 两边的字符必须都出现过偶数次. 使用哈希表把字符串都存储起来, 然后通过
(cnt/2)*2来取每个字符的个数(除法取整出现奇数次与偶数次的区别了), 每个字符都会取偶数个, 不论字符出现多少次. 由于前面都是取偶数个字符, 最后当res<str.size()表示可以再在中间添加一个出现过奇数次的字符 - 传送门 --> 给定字符串构成最长回文字符串
- leetcode --> 最长回文串
前缀树/字典树
实现字典树, 包含以下四个主要功能
void insertStr(const string word)添加word, 可重复添加void deleteStr(const string word)删除word, 如果word添加过多次, 仅删除一个int search(const string word)查询word是否在前缀树中, 返回插入次数int prefixNumber(const string pre)返回以字符串pre为前缀的单词数量
- 算法: 与样本量无关, 与样本的长度有关系. 不能把字母放在边上, 应该把字符转换为索引放到边上, 通过增加数据项来添加功能:
(1)每个节点加一个数据项, 有多少个字符串是以当前节点为结尾的, 可以统计字符串的个数
(2)每个节点加一个数据项, 有个字符串, 统计有多少个字符串以其作为前缀, 每个节点被划过多少次 - 传送门 --> 前缀树
字符串数组查找
一个字符串类型的数组arr1, 另一个字符串类型的数组arr2,
(1)arr2中有哪些字符是arr1中出现的, 打印出来 ?
(2)arr2中有哪些字符串, 是作为arr1中某个字符串前缀出现的, 打印出来
(3)arr2中有哪些字符, 是作为arr1中某个字符串前缀出现的. 请打印arr2中出现次数最大的前缀
- 传送门 --> 前缀树
子数组最大异或和
给定一个数组, 求子数组的最大异或和
- 算法1: 三个for循环, 依次定义子数组的start与end位置, 最后一个for求子数组的异或和, 时间复杂度O(N^3)
- 算法2: 与算法1相比用了两个for循环, 区别是求最大值的位置
- 算法3: 加速原理: 0~i的异或 = (0~start-1) ^ (start~i), 实际与算法2 getMaxE_2时间复杂度同是O(N^2)
- 算法4: 利用字典树的加速, 遍历数组同时遍历字典树, 由于字典树的深度为固定位数(int为32位), 所以事件复杂度O(N)
- 传送门 --> 子数组最大异或和
KMP算法详解与应用
给定两个字符串str和match, 长度分别为N和M. 实现一个算法, 如果字符串str中含有子串match, 则返回match在str中的开始位置, 不含有则返回-1
解决包含问题, 字符串str1, str2, 求str1中某一子串是否与str2一样, 若一样返回str1开始位置, str1="aaaaaab", str2="aaab"
- 算法1: 笨方法, 依次遍历str1字符然后与str2比较, 时间复杂的O(N*M), 从任何位置开题配str2都是独立的
- 算法2: KMP解决包含问题, 让前面匹配的信息指导后面. 滑动匹配
- 传送门 --> KMP
大串
把一个字符串调整为大字符串, 在这个大字符串中要求包含两个原始串
要求: 大字符串生成时只能在原始串后面添加字符串, 添加长度最短, 包含两个原始串, 开头位置不能相同, 并且大串最短
例如: 原始串abcabc 添加abc生成大串abcabcabc, 前6个abcabc, 后6个字符abcabc共包含两个原始串
- 算法: 与KMP求next数组类似, 求整体串最长前缀与最长后缀, 即最后一个位置的下一个位置的next值, 例如: abcdeabc, 最后一个位置的下一个位置的next值为3, 添加后abcdeabcdeabc
- 传送门 --> 大串
确定一个字符串不是某一字符串重复得到的
确定一个字符串不是某一字符串重复得到的. 如字符串123123123由字符串123得到
- 算法: KMP算法, next数组求到字符串长度的下一位
对于字符串str, 如果j满足, 0<=j<=n-1且str(0, j) = str(n-1-j, n-1),
令k=n-1-j, 若k整除n, 不妨设n=mk, 则s(0, (m-1)k-1)=s(k, mk-1),
即s(0, k-1)=s(k, 2k-1)= …… =s((m-1)k-1, mk-1), 即s满足题设条件
故要判断s是否为重复子串组成, 只需找到满足上述条件的j或k, 且k整除n, 即说明s满足条件, 否则不满足
利用已算出的next(n), 令k=n-next(n), 若k整除n, 且k<n, 则s满足条件, 否则不满足. 上述算法的复杂度可证明为O(n) - 传送门 --> 确定一个字符串不是某一字符串重复得到的
- leetcode --> 重复的子字符串
Manacher算法
给定一个字符串str, 返回str中最长回文子串的长度
- 算法: 任意字符间及两边插入一个任意字符(可以是出现过的), 三个概念, 回文半径数组, 回文中心, 回文右边界
回文半径数组pArr: 以每个字符串为中心, 向两边扩, 最多能扩多少个字符
回文中心(index): 对应回文半径时的中心字符
回文右边界(pR): 下一个即将扩到的位置
遍历字符串, 遍历位置i
(1) i不在回文在回文右边界, 暴力扩
(2) i在回文半径内, i的对称点i'的回文半径在当前回文左边界内, pArr[i] = pArr[2 * index - i]
(3) i在回文半径内, i的对称点i'的回文半径在当前回文左边界外, pArr[i] = pR - i
(4) i在回文半径内, i的对称点i'的回文半径当前回文左边界重合, 两边不确定, 暴力扩
- 传送门 --> Manacher
末尾添加字符串构成回文串
只能够向字符串最后添加字符, 怎么能够让字符串整体都变成回文串. 要求添加字符最少
- 算法: 使用Manache, 求必须包含最后一个字符情况下最长回文串多少. 找回文半径扩的str.size()时对应的回文半径是多少, 从str头至str.size()-maxContainsEnd+1位置取字符
- 传送门 --> 末尾添加字符串构成回文串
最长回文子串
给定一个字符串str, 找到str中最长的回文子串
贪心&动态规划&递归
切金条
一块金条切成两半, 需要花费和长度数值一样的铜板. 如长度为20的金条, 不管切成长度多大的两半, 都需要花费20个铜板. 一群人想分整块金条, 怎么分最省铜板?
例如, 给定数组{10, 20, 30}, 数组长度代表3个人, 整块金条长度为10+20+30=60. 金条要分成10, 20, 30三个部分.
如果先把金条分成10和50, 花费60, 在把长度50的金条分成20和30, 花费50, 一共花费110
如果先把金条分成30和30, 花费60, 在把长度30的金条分成10和20, 花费30, 一共花费90
- 算法: 贪心问题, 把这个数组加入到小根堆中, 每次从小根堆中拿出两个数相加后放入小根堆, 直至堆中元素只剩下一个时停止. 从底往上算, 从上向下切. 哈夫曼编码问题, 子节点合并在一起的代价是加起来的和, 代价是所有非叶子节点的和
- 传送门 --> 切金条
做项目获得最大受益
给定两个整数w和k, w代表拥有的初始资金, k代表最多可做k个项目. 再给定两个长度为N的正数数字cost[]和profits[], 代表一共有N个项目, cost[i]和profits[i]分别表示第i号项目的启动资金与做完后的利润(注意是利润, 如果一个项目启动资金为10, 利润为4, 代表该项目的最终收入为14). 一次只能做一个项目, 并且手里拥有自己大于或等于某个项目的启动资金时, 才能做这个项目. 该如何选择做项目, 可以使最终的受益最大
说明: 每做完一个项目, 马上获得的收益, 可以支持你去做下
- 算法:
(1)把cost和profits对应点结合起来自定义一个项目类型node, 把所有node以cost为标准构建一个小根堆minCostQ, 把所有项目压入小根堆
(2)循环k次, 把minCostQ中s小于现有资金的项目取出压入以profit为标准的大根堆maxProfitQ, 利润与本金相加 - 传送门 --> 做项目获得最大受益
宣讲会安排项目
一些项目要占用一个会议室宣讲, 会议室不能同时容纳两个项目的宣讲. 给你每一个项目开始的时间和结束的时间(给你一个数组, 里面是一个个具体的项目), 安排宣讲的日程.
要求会议室进行的宣讲的场次最多. 返回这个最多的宣讲场次.
- 算法: 贪心策略:
(1)项目开始早的先安排, 可举出反例, 6点全天, 这样无法安排其他项目了, ×
(2)会以持续时间段先安排, 如三个项目, 其中两个间隔小于剩余持续时间最短项目, 但安排最短时间项目后另外两个项目无法安排了, ×
(3)结束时间早的先安排, 淘汰同属于这个时间段的其他项目 √ - 传送门 --> 宣讲会安排项目
n的阶乘
依赖顺序逆着回去就是计算顺序
- 传送门 --> n的阶乘
汉诺塔
- 算法1: (1)1~n-1借助to, 从from移到help上; (2)剩1个移动到to上; (3)1~n-1借助from, 从help移动到to上
- 算法2: 定义出6个过程, 彼此间嵌套
- 传送门 --> 汉诺塔
牛问题
母牛每年生一只母牛, 新出生的母牛成长三年后也能每年生一只母牛, 假设不会死.
求N年后, 母牛的数量
如果每只母牛只能活10年, 求N年后母牛的数量
- 算法: F(n)=F(n-1)+F(n-3), 存在O(logN)解法, 待续
- 传送门 --> 牛问题
暴力递归改动态规划
所有动态规划都是从暴力版本优化而来, 空间换时间傻白甜问题
有些方法改不出动态规划, 如汉诺塔, 因为没有重复计算
暴力递归改动态规划, 哪些问题可以改, 哪些问题不可以改
面试过程中没见过的动态规划都是从暴力递归修改而来
汉诺塔, 要求打印所有步骤, 有后效性问题, 所以改不出动态规划
用一种机制, 把递归过程中的用到的数据做一个缓存记录下来, 再用到数据时, 不递归而是直接从缓存中拿取数据, 记忆化搜索放法
递归展开过程中有重复状态, 而且重复状态与到达它的路径无关, 无后效性问题
- 写出尝试版本, 即暴力方法
- 分析可变参数, 哪几个可变参数可以代表返回值的状态
- 可变参数几维, 动态规划表就是几维
- 查找终止状态, base case值设置好
- 普遍位置需要哪些位置, 逆着回去就是填表的顺序
最小的路径和
一个二维数组, 二维数组中的每个数都是正数, 要求从左上角走到右下角, 每一步只能向右或者向下. 沿途经过的数字要累加起来. 要求返回最小的路径和
- 算法1: 暴力递归, 依次递归当前节点与有边节点和, 当前节点与下边节点的和, 递归结束条件为到达右下角
- 算法2: 动态规划, 右下角到当前位置的路径和与之前走过的路径无关, 状态参数确定返回值确定, 即当row和col确定返回值确定, 无后效性问题, 可以改动态规划
可变参数为row和col, row和col的变化范围就是返回值的变化范围, 以row和col为行和列建立一张二维表, 查看哪些位置的值不依赖其他位置, base case(一个为题划分到什么程度就不用向下划分了)最右下角位置 - 传送门 --> 最小的路径和
- 牛客 --> 矩阵中的路径
数组累加和
一个数组arr, 和一个整数aim. 如果可以任意选择arr中的数字, 能不能累加得到aim, 返回true或者false
- 算法1: 暴力递归, 要当前数字和不要当前数字, 同前面字符串子序列一样
- 算法2: 动态规划, arr固定, aim固定, 可变参数i位置及其累加和sum不确定(目前只能处理正数数组, 若含负数数组扩充二维表, 列数扩充负向最小值到正向最大值?)
建立二维表, 有多少个数就有多少个i, sum所有数累加起来, 如arr = {3, 2, 5}, aim = 7, 最优一行7位置为T其他位置为F
X 0 1 2 3 4 5 6 7 8 9 10
0 T F T F T T F T F F F arr[0] = 3
1 T F T F F T F T F F F arr[1] = 2
2 F F T F F F F T F F F arr[2] = 5
3 F F F F F F F T F F F - 传送门 --> 数组累加和
背包问题
给定两个数组w和v, 两个数组长度相等, w[i]表示第i件商品的重量, v[i]表示第i件商品的价值. 再给定一个整数bag, 要求你挑选商品的重量加起来一定不能超过bag, 返回满足这个条件下, 你能获得的最大价值
- 算法1: 暴力递归, 要当前的w[i]和v[i]和不要当前w[i]和v[i]两种情况讨论, 返回条件超重和到达数组末端. 模式同前面字符串子序列一样
- 算法2: 动态规划, 以bag建立二维表, 同数组累加以aim为列建立二维表类似, 偏移量变为weights数组, 有些疑问
- 传送门 --> 背包问题
大数据
如何判断一个数是否在40亿个整数中
如何只用2GB内存从20/40/80亿个整数中找到出现次数最多的数
20亿
面试官: 如果我给你 2GB 的内存, 并且给你 20 亿个 int 型整数, 让你来找出次数出现最多的数, 你会怎么做?
小秋: (嗯?怎么感觉和之前的那道判断一个数是否出现在这 40 亿个整数中有点一样?可是, 如果还是采用 bitmap 算法的话, 好像无法统计一个数出现的次数, 只能判断一个数是否存在) , 我可以采用哈希表来统计, 把这个数作为 key, 把这个数出现的次数作为 value, 之后我再遍历哈希表哪个数出现最多的次数最多就可以了.
面试官: 你可以算下你这个方法需要花费多少内存吗?
小秋: key 和 value 都是 int 型整数, 一个 int 型占用 4B 的内存, 所以哈希表的一条记录需要占用 8B, 最坏的情况下, 这 20 亿个数都是不同的数, 大概会占用 16GB 的内存.
面试官:你的分析是对的, 然而我给你的只有 2GB 内存.
小秋: (感觉这道题有点相似, 不过不知为啥, 没啥思路, 这下凉凉) , 目前没有更好的方法.
面试官: 按照你那个方法的话, 最多只能记录大概 2 亿多条不同的记录, 2 亿多条不同的记录, 大概是 1.6GB 的内存.
小秋: (嗯?面试官说这话是在提示我?) 我有点思路了, 我可以把这 20 亿个数存放在不同的文件, 然后再来筛选.
面试题:可以具体说说吗?
小秋:刚才你说, 我的那个方法, 最多只能记录大概 2 亿多条的不同记录, 那么我可以把这 20 亿个数映射到不同的文件中去, 例如, 数值在 0 至 2亿之间的存放在文件1中, 数值在2亿至4亿之间的存放在文件2中…., 由于 int 型整数大概有 42 亿个不同的数, 所以我可以把他们映射到 21 个文件中去. 显然, 相同的数一定会在同一个文件中, 我们这个时候就可以用我的那个方法, 统计每个文件中出现次数最多的数, 然后再从这些数中再次选出最多的数, 就可以了.
面试官:嗯, 这个方法确实不错, 不过, 如果我给的这 20 亿个数数值比较集中的话, 例如都处于 1~20000000 之间, 那么你都会把他们全部映射到同一个文件中, 你有优化思路吗?
小秋:那我可以先把每个数先做哈希函数映射, 根据哈希函数得到的哈希值, 再把他们存放到对应的文件中, 如果哈希函数设计到好的话, 那么这些数就会分布的比较平均. 数字过于集中可以直接在内存中统计
40亿级别
面试官:那如果我把 20 亿个数加到 40 亿个数呢?
小秋:最开始用21个文件是因为整型范围是42以内, 给40个整数还是再42亿以内, 还是可以用21个文件解决
面试官:那如果我给的这 40 亿个数中数值都是一样的, 那么你的哈希表中, 某个 key 的 value 存放的数值就会是 40 亿, 然而 int 的最大数值是 21 亿左右, 那么就会出现溢出, 你该怎么办?
小秋: (那我把 int 改为 long 不就得了, 虽然会占用更多的内存, 那我可以把文件分多几份呗, 不过, 这应该不是面试官想要的答案) , 我可以把 value 初始值赋值为 负21亿, 这样, 如果 value 的数值是 21 亿的话, 就代表某个 key 出现了 42 亿次了。
80亿级别
面试官:如果把 40 亿增加到 80 亿呢?
小秋: (我靠, 这变本加厉啊) ………我知道了, 我可以一边遍历一遍判断啊, 如果我在统计的过程中, 发现某个 key 出现的次数超过了 40 亿次, 那么, 就不可能再有另外一个 key 出现的次数比它多了, 那我直接把这个 key 返回就搞定了。
内存池
最大公约数/最小公倍数
- 算法: 最小公约数就是交叉相模. 最小公倍数=两数成绩/最大公约数
- 传送门 --> 最小公倍数
n&(n-1)
统计二进制中1的个数与判断是否是2的倍数
- 传送门 --> n与n-1


