求解迷宫问题
问题:
问题描述:
有一个8×8 的迷宫图,其中O表示通路方块X表示障碍方块。假设入口位置为(0,0),出口为右下角方块位置 (7,7)。设计一个程序求指定入口到出口的一条迷宫路径。
输入描述:
8 行,每行 88 个字符表示迷宫。
样例输入:
OXXXXXXX
OOOOOXXX
XOXXOOOX
XOXXOXXO
XOXXXXXX
XOXXOOOX
XOOOOXOO
XXXXXXXO
样例输出:
XXXXXXX
OOOXXX
X XXOOOX
X XXOXXO
X XXXXXX
X XX X
X X
XXXXXXX
思考:
这题花了好长好长时间,分析了下原因:.我没在网上找到完全一样的题,只能看相似的题改编别人的题解2.我压根不会深度搜索,也不会什么记忆化,即便最后写出来了题目,也有很大的运气成分。3.这题虽然有看题解,但其实我自己也还是花了很多心思的,在不断的错误中理清思路。
这道题用到了递归,深度搜索。当然还有别的做法,我没尝试,我同学提醒我在《数据结构》P50页有相同的题,看了下,是利用栈写的。
在想着解题之前,我认为有些小的问题是需要考虑和解决的,在看题解之前,我连这些小问题都无法解决,所以这里将他们单独罗列出来。
1.用字符串数组存储OX想必人人都知道,不过该怎么模拟前进方向呢,这里采用的是设置一个位置数组int pos[] = {-1, 0, 1, 0, -1},从下标0开始每次从中连续取两个数,一直到下标3为止,这样刚好取出了(-1,0),(0,1),(1,0),(0,-1)四个坐标,可以模拟四个方向,对我这个新手而言真的非常巧妙。
2.该如何记录自己走过的路径呢?这里采用的是一个bool型二维数组,用1表示走过的路,0表示未走过的和障碍物。
接下来是如何进行深度搜索的过程了,也就是dfs函数的工运行过程,这里我恐怕讲不明白,但是通过看函数代码并把样例中的数据模拟运行一遍就可以很容易的理解了,此外,在调试代码的时候,我保留了一份每调用一次递归就打印已走路径的代码,可以通过运行这份代码加速理解,我将其放在代码1中。
写给自己看的
在调试代码中过程,我遇见了一个坑,这个坑恐怕也只有我才会遇见,因为我比较呆,我有必要记录提醒自己一下。最初,我一直是想将打印最终结果的函数放在主函数里写的,但是不行。
for (int m = 1; m < N; m++)
{
for (int n = 1; n < N; n++)
cout << path[m][n] << " ";
cout << endl;
}
就是这段代码,后来我把它放在了找到出口的时候(x==8&&y==8)。解释下为什么不能放在主函数里,如果你在dfs函数全部调用结束后在主函数中调用一下打印bool类型二维数组的代码,你会发现这样的结果
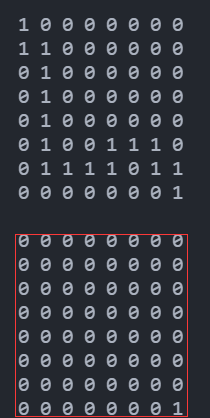
bool型二维数组在主函数中打印只有(8,8)的值为1,其他都是0,但是在dfs函数中最后一次打印却是正常的。
这是为什么呢,我粗粗地想了一下,觉得应该是因为path[x][y] = true;dfs(l, w);path[x][y] = false;中path[x][y] = false的原因,当执行完if (x == 8 && y == 8)里的语句后,最后一次递归结束,开始执行退栈操作,而每退一次栈后就将执行path[x][y]=false这条代码,把之前被修改成true的二维数组又改回了false😂。
代码:
输入数据就是上面的样例
代码1:(学习版)
点击查看代码
#include <iostream>
using namespace std;
const int N = 9;
char map[N][N];
int pos[] = {-1, 0, 1, 0, -1};
bool path[N][N];
void dfs(int x, int y);
int main()
{
for (int i = 1; i < N; i++)
{
for (int j = 1; j < N; j++)
{
map[i][j] = getchar();
}
getchar();
}
dfs(1, 1);
cout << endl;
for (int m = 1; m < N; m++)
{
for (int n = 1; n < N; n++)
cout << path[m][n] << " ";
cout << endl;
}
return 0;
}
void dfs(int x, int y)
{
getchar();
if (x == 8 && y == 8)
{
path[x][y] = true;
for (int m = 1; m < N; m++)
{
for (int n = 1; n < N; n++)
cout << path[m][n] << " ";
cout << endl;
}
return;
}
int l, w;
for (int i = 0; i < 4; i++)
{
l = x + pos[i], w = y + pos[i + 1];
if (l > 0 && w > 0 && l < N && w < N && map[l][w] == 'O' && path[l][w] == false) //路通吗?
{
cout << x << "," << y << endl;
path[x][y] = true;
for (int m = 1; m < N; m++)
{
for (int n = 1; n < N; n++)
cout << path[m][n] << " ";
cout << endl;
}
dfs(l, w);
path[x][y] = false;
}
}
return;
}
// OXXXXXXX
// OOOOOXXX
// XOXXOOOX
// XOXXOXXO
// XOXXXXXX
// XOXXOOOX
// XOOOOXOO
// XXXXXXXO
代码2:(AC版)
点击查看代码
#include <iostream>
using namespace std;
const int N = 9;
char map[N][N];
int pos[] = {-1, 0, 1, 0, -1};
bool path[N][N];
void dfs(int x, int y);
int main()
{
for (int i = 1; i < N; i++)
{
for (int j = 1; j < N; j++)
{
map[i][j] = getchar();
}
getchar();
}
dfs(1, 1);
return 0;
}
void dfs(int x, int y)
{
if (x == 8 && y == 8)
{
path[x][y] = true;
for (int m = 1; m < N; m++)
{
for (int n = 1; n < N; n++)
{
if (path[m][n] == true)
cout << " ";
else
cout << map[m][n];
}
cout << endl;
}
return;
}
int l, w;
for (int i = 0; i < 4; i++)
{
l = x + pos[i], w = y + pos[i + 1];
if (l > 0 && w > 0 && l < N && w < N && map[l][w] == 'O' && path[l][w] == false) //路通吗?
{
path[x][y] = true;
dfs(l, w);
path[x][y] = false;
}
}
return;
}
// OXXXXXXX
// OOOOOXXX
// XOXXOOOX
// XOXXOXXO
// XOXXXXXX
// XOXXOOOX
// XOOOOXOO
// XXXXXXXO


 浙公网安备 33010602011771号
浙公网安备 33010602011771号