整数分解
https://www.acwing.com/problem/content/description/1595/
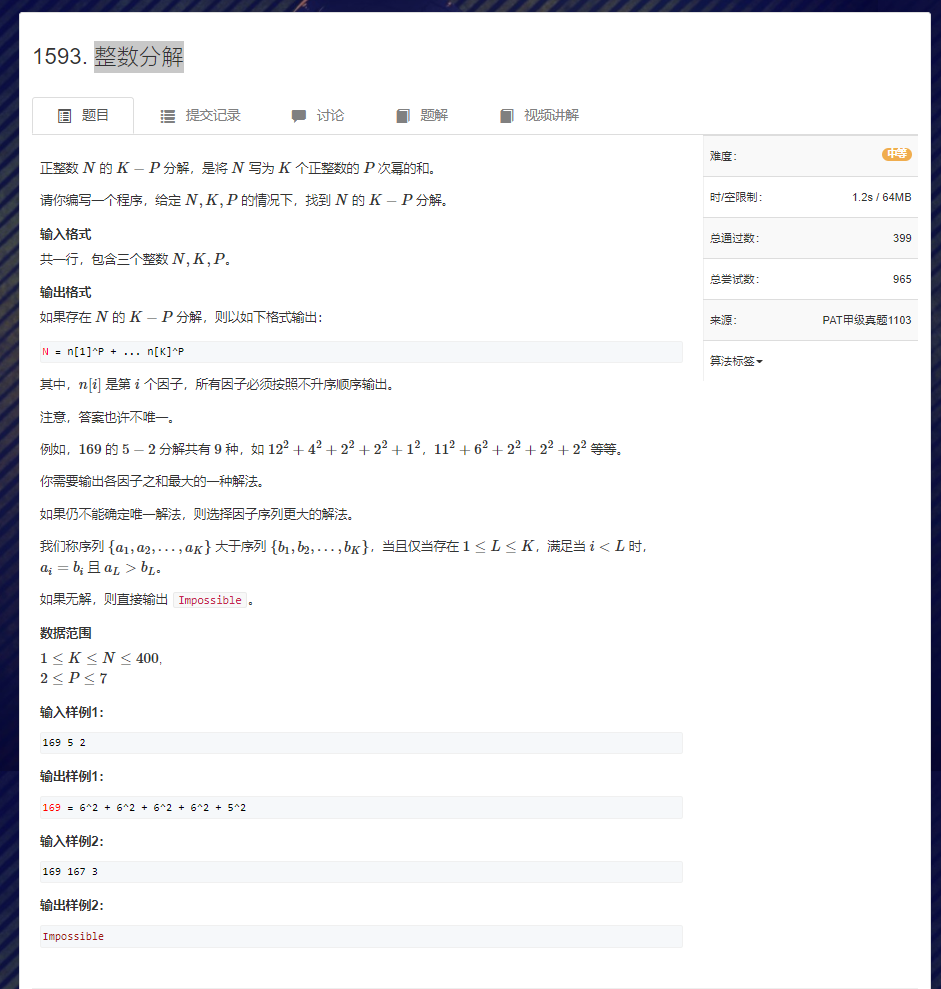
dp解法
#include <iostream>
#include <cstring>
using namespace std;
const int N = 410;
int n, k, p;
int f[21][N][N];
int power(int a, int b)
{
int res = 1;
for (int i = 0; i < b; i ++ ) res *= a;
return res;
}
int main()
{
cin >> n >> k >> p;
memset(f, -0x3f, sizeof f);
f[0][0][0] = 0;
int m;
for (m = 1; ; m ++ )
{
int v = power(m, p);
if (v > n) break;
for (int i = 0; i <= n; i ++ )
for (int j = 0; j <= k; j ++ )
{
f[m][i][j] = f[m - 1][i][j];
if (i >= v && j) f[m][i][j] = max(f[m][i][j], f[m][i - v][j - 1] + m);
}
}
m -- ;
if (f[m][n][k]<0) puts("Impossible");
else
{
printf("%d = ", n);
bool is_first = true;
while (m)
{
int v = power(m, p);
while (n >= v && k && f[m][n - v][k - 1] + m >= f[m-1][n][k])
{
if (is_first) is_first = false;
else printf(" + ");
printf("%d^%d", m, p);
n -= v, k --;
}
m -- ;
}
}
return 0;
}
dfs写法
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
int n, k, p;
int v[21];
int resSum = -1;
vector<int> path, ans;
/* i:当前递归到的因子数,n:选取的因子数i^p的和(初始化为n,每一步减去v[i]),
cnt:选取的因子数的个数,sum:选取的因子数之和 */
void DFS(int i, int n, int cnt, int sum) {
if (n == 0 && cnt == k) {
if (sum > resSum) {
resSum = sum;
ans = path;
}
return;
}
while (i > 0) {
//减枝,防止递归爆栈
if (n - v[i] >= 0 && cnt + 1 <= k) {
path[cnt] = i;
DFS(i, n - v[i], cnt + 1, sum + i);
}
i--;
}
}
int main() {
cin >> n >> k >> p;
path.resize(k);
int i = 0;
while (pow(++i, p) <= n){
//用数组存入i^p的值
v[i] = pow(i, p);
}
i--;
DFS(i, n, 0, 0);
if (resSum == -1) puts("Impossible");
else {
printf("%d = %d^%d", n, ans[0], p);
for (int i = 1; i < ans.size(); i++) {
printf(" + %d^%d", ans[i], p);
}
cout << endl;
}
return 0;
}

