Codeforces Round #841 (Div. 2) and Divide by Zero 2022（A-D）

Codeforces Round #841 (Div. 2) and Divide by Zero 2022（A-D）

题目	链接	限制
A	Joey Takes Money	standard input/output1 s, 256 MB
B	Kill Demodogs	standard input/output1 s, 256 MB
C	Even Subarrays	standard input/output2.5 s, 256 MB
D	Valiant's New Map	standard input/output2 s, 256 MB

综述

题目有一点点不友好，对于D，竟然....

但是总的难度还行

补题

A Joey Takes Money

​

​

​

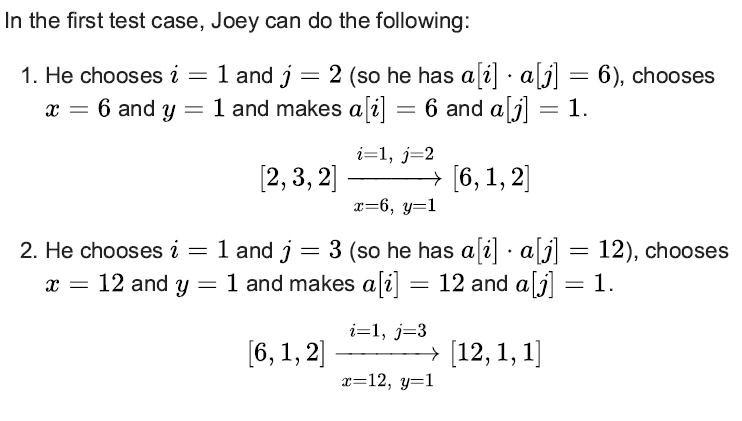
input

3
3
2 3 2
2
1 3
3
1000000 1000000 1

output

28308
8088
2022000000004044

题目大意

给定一个数组，有下列操作

• 选择两个数字 i 和 j (1≤i<j≤n)
• 选择两个整数 x 以及 y，使得x⋅y=ai⋅aj
• 然后使用x替换ai，使用y替换aj

可以使用任意数目的以上操作，使得所有的数字加起来最大。

思路

根据样例，可以猜想，最后把n-1个元素变为1，然后相加起来是最大的。

（贪心）证明：

假设有两个数字不是1，那么他们的值一定大于1，设两个数字为a, b

然后我：a --> a*b, b --> 1比较变化之前以及变化之后的数字大小：

\[a+b-(a\times b - 1) = (a-1)(1-b) \]

很小于1

所以变化之后更大。

代码

#include <bits/stdc++.h>
using namespace std;;
#define N 55
typedef long long ll;
ll a[N];
int n;

int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        scanf("%d", &n);
        for(int i = 1; i <= n; i++) scanf("%lld", a+i);
        ll ans = 1;
        for(int i = 1; i <= n; i++) ans *= a[i];
        ans += n - 1;
        ans *= 2022;
        printf("%lld\n", ans);
    }
    return 0;
}

B Kill Demodogs

​

​

input

4
2
3
50
1000000000

output

14154
44484
171010650
999589541

题目大意

给定一个 \(n\times n\) 的矩阵，主角开始在\(（1，1）\)处，目的地在\((n, n)\)处。

在每一个单元格上都有怪兽，在第 i 个单元格上的怪兽数量是 \(i\times j\).

主角只能向下或者是向右移动。

问：主角最多杀死多少个怪兽。

在这一道题目中，矩阵显然关于斜对角线具有对称性，所以我们选择右上角的观察

​

先凭借知觉，我们观察到，好像中间的数字比较大，所以我们尽可能沿着中间的路走

所以猜想路线：右-下-右-下....

（贪心）证明：

由于每一个格子上的怪兽数目是 \(i\times j\)

现在我们假设最优解不是我们设想的路径。

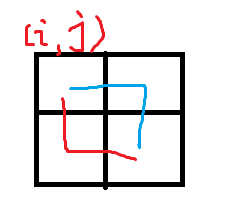
现在到达（i+1, j+1）有两种路径。

比较通过蓝色路径以及通过红色路径的大小

蓝色路径：\(i(j+1)\)

红色路径：\((i+1)j\)

作差：\(i(j+1) - (i+1)j = i - j\)

现在假如 j 大于 i ，那么我们就应该走红色路径。

就这样，对于不是最优解的情况，我们可以使用这一种方法不断变成我们的假设。所以我们的假设就是最优解。

然后计算的话就是

\[maxv = \sum_{i=1}^{n}i^2 + \sum_{n=1}^{n-1}i(i+1) = \sum_{i=1}^{n}i^2 + \sum_{i=1}^{n-1}i^2+\sum_{i=1}^{n-1}i \]

由于n最大是\(10^9\)，所以应该使用公式计算

补充相关的数学公式

​

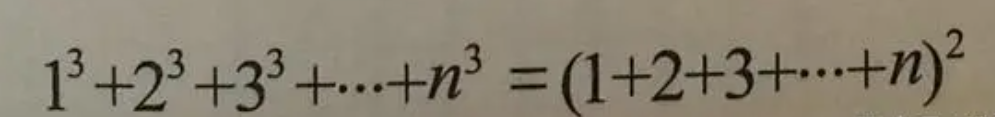
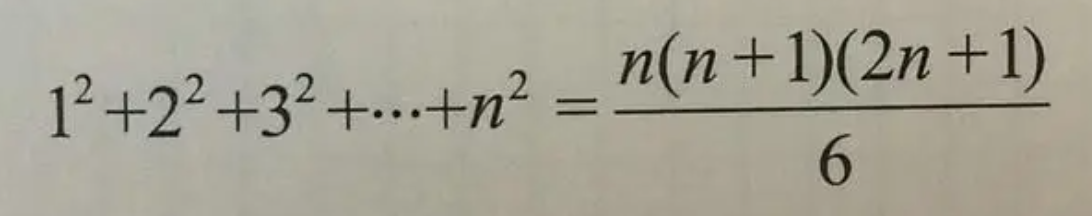
tim = int(input())
for T in range(tim):
    n = int(input())
    ans = 0
    ans += n*(n+1)*(2*n+1)//6
    ans += (n-1)*n*(2*n-1)//6
    ans += n*(n-1)//2
    ans = ans*2022%1000000007
    print(ans)

其实除法取模（除法逆元）也很简单

前提：

1. 确保取模的哪一个数字是质数
2. 确保可以整除

所以有 \(a/b = a*b^{mod-2} \%mod\)

C Even Subarrays

​

​

​

input

4
3
3 1 2
5
4 2 1 5 3
4
4 4 4 4
7
5 7 3 7 1 7 3

output

4
11
0
20

思路

这一道题目着实很妙。

首先：因数个数是奇数个的数字是非完全平方数。

但是非完全平方数比较多，我们考虑反方面：完全平方数！

首先，要是真的来枚举这一个区间，是不可行的。

对于一个区间来想，可能不是太清晰，所以可以利用前缀和思想，把区间问题转化为端点问题。

sum[L-1] XOR sum[R] == a[L] OXR .....XOR a[R]

然后我们可以枚举R，当务之急就是找到在R之前有多少个前缀与sum[R]异或之后的值是非完全平方数（枚举一遍非完全平方数）。

我们开一个数组cnt[x]记录在R之前的所有前缀中值为x的个数。

然后就可以O(1)求出个数。

总体时间复杂度为O(n*sqrt(2n))

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define N 200200
int a[N];
int sum[N];// a的前缀数组
int cnt[N*2];// 两个小于n的数进行异或，值最大不超过2N
signed main()
{
    int T;
    cin >> T;
    while(T--)
    {
        int n;
        scanf("%lld", &n);
        for(int i = 1; i <= n; i ++){
            scanf("%lld", a+i);
        }
        int ans = 0;// 答案的反面
        for(int i = 1; i <= n; i++){
            sum[i] = sum[i-1] ^ a[i];
      
        }
        cnt[0] = 1;
        // 这是因为如果sum[R] == 完全平方数，那么其实选择从1到R就可以，所以cnt[0]应该为1
        for(int i = 1; i <= n; i++){
            for(int x = 0; x * x <= 2*n; x++){
                int t = (x*x) ^ sum[i];
                if(t > 2 * n) continue;//因为x * x <= 2*n,所以可能整出来大于2n的
                ans += cnt[t];
            }
            cnt[sum[i]] ++;
        }
      
        printf("%lld\n", (long long)n * (n+1)/2 - ans);
        for(int i = 0; i <= n; i++) {
            sum[i] = 0;
        }
        for(int i = 0; i <= n * 2; i++){
            cnt[i] = 0;
        }
    }

    return 0;
}

D Valiant's New Map

​

​

input

4
2 2
2 3
4 5
1 3
1 2 3
2 3
4 4 3
2 1 4
5 6
1 9 4 6 5 8
10 9 5 8 11 6
24 42 32 8 11 1
23 1 9 69 13 3
13 22 60 12 14 17

output

2
1
1
3

题目大意

给定一个\(n\times m\)的矩阵，求一个最大值l，使得在矩阵中存在有 \(l\times l\) 的方格中的最小值大于等于 l

思路

首先容易证明具有单调性:

如果可以找到使得在矩阵中存在有 \(l\times l\) 的方格中的最小值大于等于 l，那么我就在这片区域中一定能找到 \(m\times m\) 的方格中的最小值大于等于 m (\(m\le l\))

然后问题就成了这样：给定一个框的大小，求有没有一种框法，使得框柱的数字的最小值是给定值。

如果暴力显然时间不够用，但是最小值又不能合起来表示（以一部分的最小值表示）。

但是这里我们的给定值是一个固定的值，所以我们并没有必要知道某一个区域中的最小值是多少，而是仅仅需要知道这一个区域的最小值是不是小于给定值就可以了。

所以我建立一个二维前缀和，如果大于等于给定值，那么我们假想值为0，否则值为1

然后查询前缀和中的值是不是0就可以判断这一种框法是否可行。

但是

这一道题目恶心在数组必须动态开

为此有两种方法：

• 动态内存分配（额...）

    int **a = (int **)calloc(n, sizeof(int*));
    for(int i = 0; i < n; i++) a[i] = (int *)calloc(m, sizeof(int));

别忘了之后还要free!!

注意：开辟后自动有初始值0

• 使用vector来实现

resize会分配空间，并且自动初始化为0

也可以resize(大小， 初始值)

shrink_to_fit()可以让已经分配的内存空间缩小到size的大小

#include <bits/stdc++.h>
using namespace std;
int n, m;
#define N 1100000
bool ck(int mid, int **a, int ** f)
{
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            f[i][j] = f[i-1][j] + f[i][j-1] - f[i-1][j-1] + (a[i][j] < mid);
            // printf("%d ", f[i][j]);
        }
        // puts("");
    }
    for(int i = mid; i <= n; i++){
        for(int j = mid; j <= m; j++){
            if(f[i][j] - f[i - mid][j] - f[i][j - mid] + f[i-mid][j-mid] == 0) return true;
        }
  
    }
    return false;
}
int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d%d", &n, &m);
        //int *a[m + 1] = (int *[m+1])calloc((n+1)*(m+1), sizeof(int));int** p = (int **)malloc(3*sizeof(int*));//申请指针数组
 
        int** a = (int **)malloc((n+1)*sizeof(int*));
 
        for(int i=0; i<n+1; i++)
        {
            a[i] = (int*)malloc((m+1)*sizeof(int));
        }

    	int** f = (int **)malloc((n+1)*sizeof(int*));
  
        for(int i=0; i<n+1; i++)
        {
            f[i] = (int*)malloc((m+1)*sizeof(int));
        }

        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= m; j++)
            {
                scanf("%d", &a[i][j]);
            }
        }

        int l = 1, r = min(n, m);
        while(l < r)
        {
            int mid = (l + r + 1) >> 1;
            if(ck(mid, a, f)) l = mid;
            else r = mid - 1;
        }  
        printf("%d\n", l);
       for(int i=0; i<n+1; i++)
        {
            free(f[i]);
            free(a[i]);
        } 
        free(a);
        free(f);
    }
    return 0;
}